Công thức Chu vi hình Thoi & Cách tính đơn giản 2023

Hình thoi được biết đến là một trong những kiến thức Toán học quan trọng, đặc biệt là đối với các bạn học sinh lớp 4. Vậy hình thoi là gì và cách tính chu vi của nó ra sao?

Để củng cố kiến thức đã học, ngay sau đây đội ngũ INVERT chúng tôi sẽ hướng dẫn bạn biết hình thoi là gì, công thức tính chu vi hình thoi & cách sử dụng nó vô cùng chi tiết, dễ hiểu thông qua bài viết sau.

I. Hình thoi là gì? Chu vi hình thoi là gì?

Hình thoi trong hình học Euclide được định nghĩa là tứ giác có 4 cạnh bằng nhau. Hình thoi cũng là hình bình hành có 2 cạnh kề bằng nhau hay hình bình hành có 2 đường chéo vuông góc với nhau.

Chu vi hình thoi là tổng độ dài các đường bao quanh hình hay đường bao quanh toàn bộ diện tích hình đó.

Tính chất của hình thoi:

• Các góc đối nhau bằng nhau.
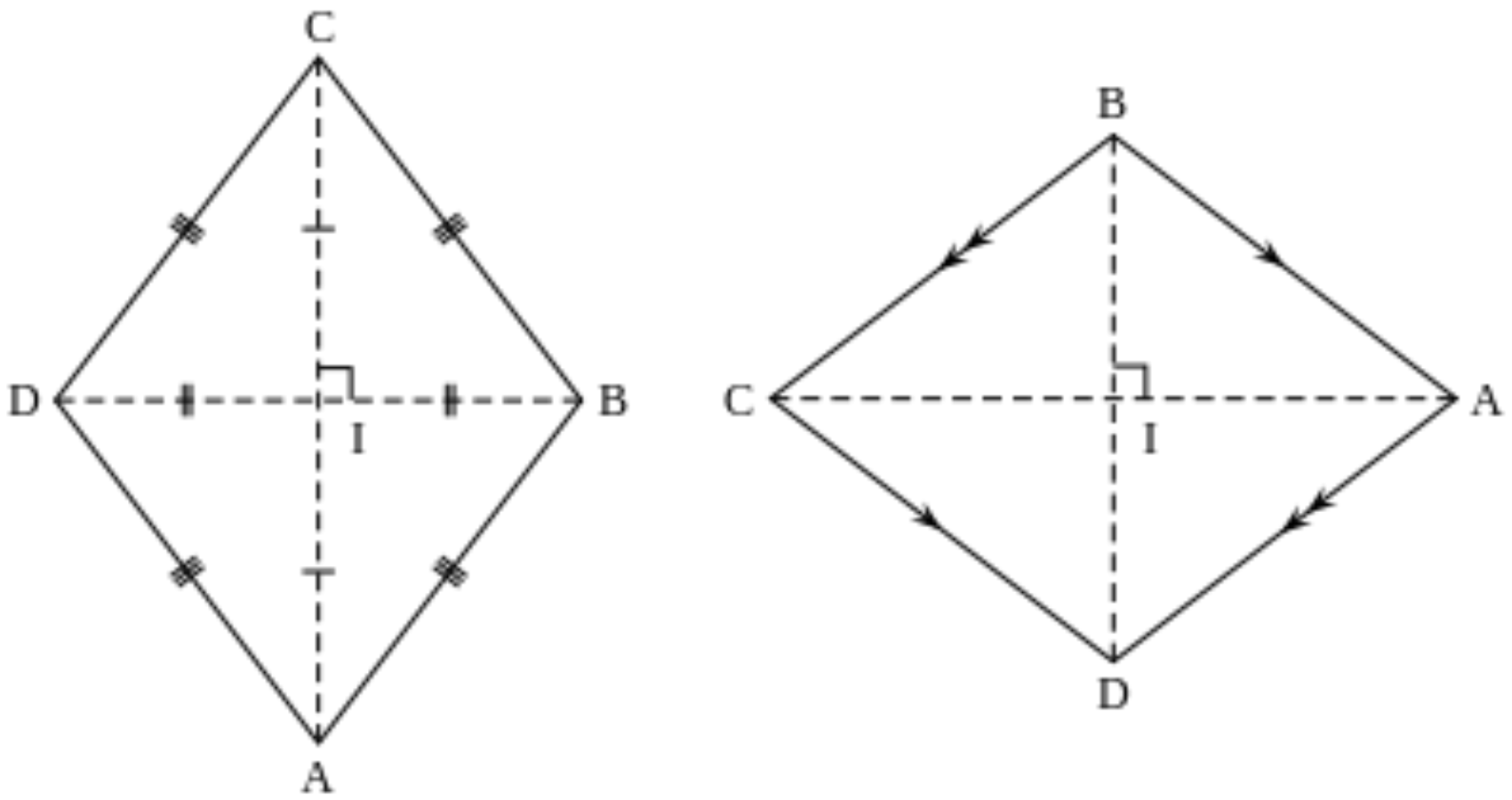
• Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
• Hai đường chéo là các đường phân giác của các góc của hình thoi.
• Hình thoi có tất cả tính chất của hình bình hành.

II. Công thức tính chu vi hình thoi

Chu vi hình thoi được tính bằng độ dài cạnh hình thoi nhân với 4.

Công thức: P = a x 4

Mở rộng: Nếu biết chu vi hình thoi, để tìm cạnh hình thoi ta lấy chu vi chia 4.

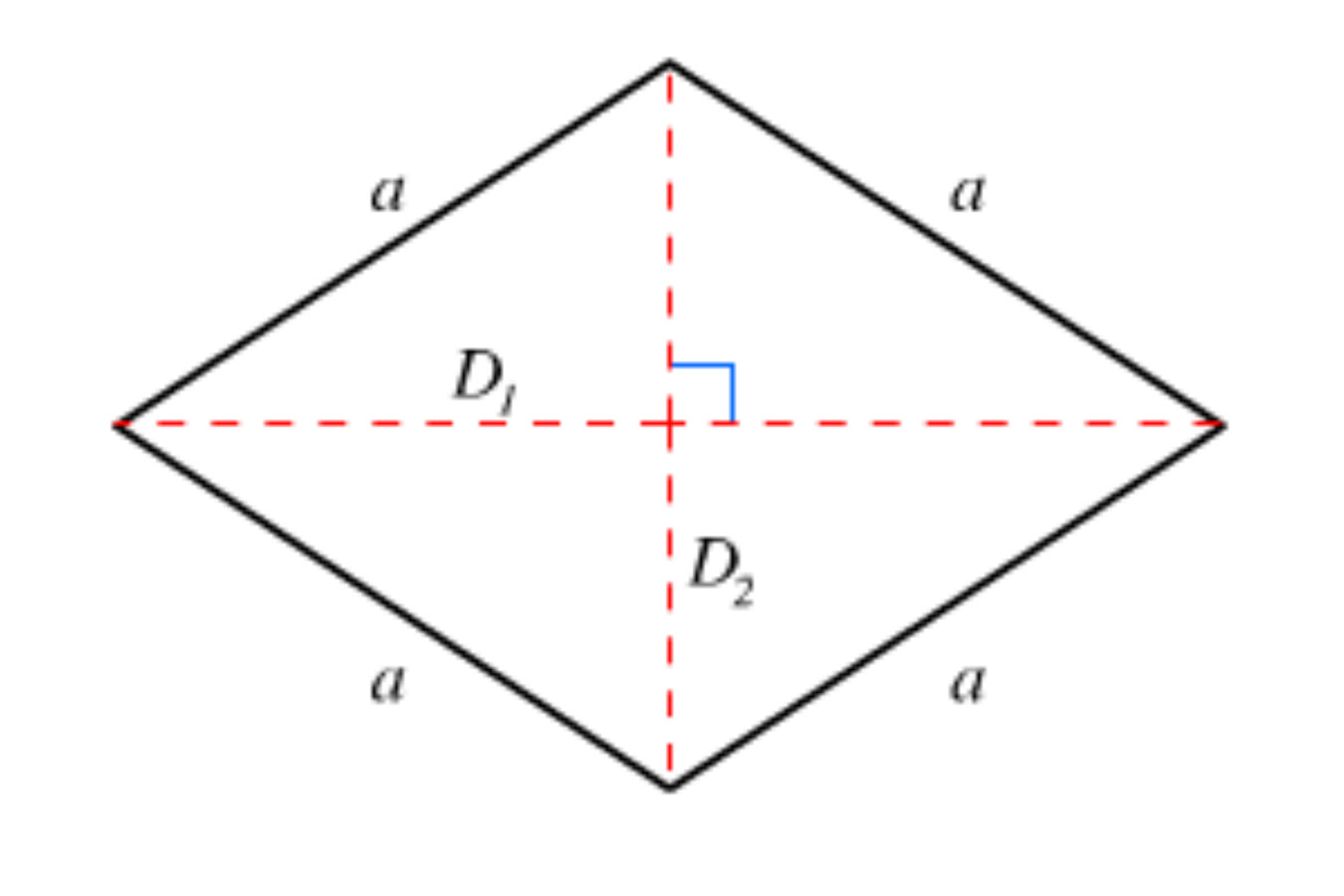
Trong đó:

• P: chu vi hình .
• a: chiều dài của cạnh hình thoi.

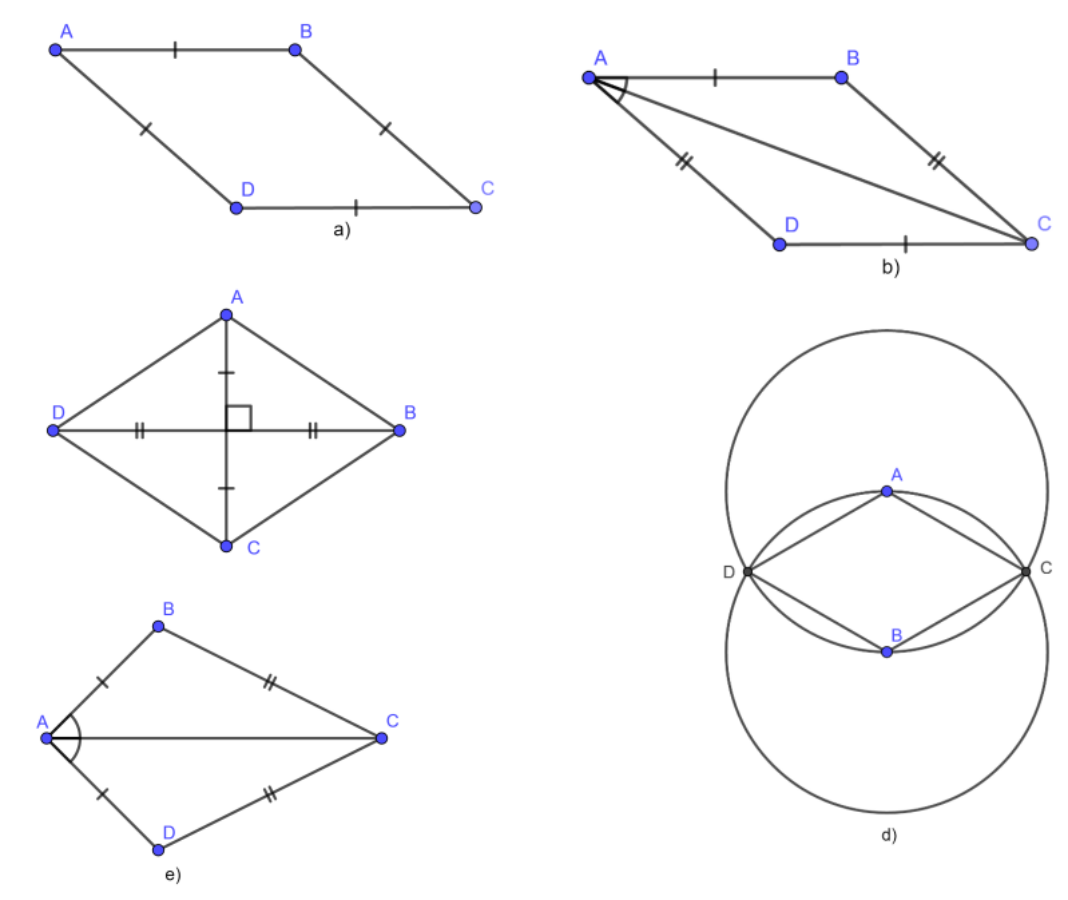
III. Dấu hiệu nhận biết hình thoi

Hình tứ giác đặc biệt là hình thoi khi:

• Tứ giác có 4 cạnh bằng nhau.
• Tứ giác có 2 đường chéo là đường trung trực của nhau.
• Tứ giác có 2 đường chéo là đường phân giác của cả 4 góc.

Hình bình hành đặc biệt: Hình thoi là dạng đặc biệt của hình bình hành vì nó có đầy đủ tính chất của hình bình hành và còn có một số tính chất khác:

• Hình bình hành có 2 cạnh kề bằng nhau.
• Hình bình hành có 2 đường chéo vuông góc với nhau.
• Hình bình hành có 1 đường chéo là đường phân giác của 1 góc.

IV. Một số bài tập tính chu vi hình thoi

1. Bài tập tính chu vi hình thoi có lời giải

Câu 1: Tính chu vi của hình thoi, biết độ dài cạnh lần lượt là:

a) 9 cm

b) 20 dm

c) 3/4 m

d) 5, 6 cm

Giải:

a) Chu vi của hình thoi là: 9 x 4 = 36 (cm)

b) Chu vi của hình thoi là: 20 x 4 = 80 (dm)

c) Chu vi của hình thoi là: 3/4 x 4 = 4 (m)

d) Chu vi của hình thoi là: 5, 6 x 4 = 22, 4 (cm)

Câu 2: Tính chu vi của hình thoi biết độ dài cạnh = 10 dm.

Giải: Chu vi hình thoi đó là: 10 x 4 = 40 (dm)

Câu 3: Tính chu vi hình thoi ABCD khi biết độ dài cạnh là 7cm

Giải: Chu vi hình thoi ABCD bằng: P (ABCD) = 4 x 7 = 28 (cm)

Câu 4: Tính độ dài các cạnh của hình thoi ABCD khi biết chu vi hình thoi là 60cm

Giải: Gọi a là độ dài các cạnh của hình thoi.

Chu vi hình thoi ABCD = 4 x a = 60cm

Độ dài 1 cạnh của hình thoi là 60/4 = 15 cm

Đáp án: Độ dài một cạnh của hình thoi ABCD là 15 cm

Câu 5: Tính chu vi hình thoi biết các đường chéo bằng 16 cm và 30cm

Giải: Gọi cạnh hình thoi bằng a, các đường chéo lần lượt là d1 và d2

– Áp dụng định lý Py – ta – go trong tam giác vuông bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Ta có: a2 = (d1/2)2 + (d2/2)2= (8)2 + (15)2 hay a = 17

Chu vi hình thoi: P = 4 x a = 68.

Câu 6: Cho hình thoi ABCD , biết AB = 15 cm . chu vi hình thoi ABCD là ?

Giải: Chu vi hình thoi ABCD là: 15 × 4 = 60 (cm). Đáp số: 60cm

Câu 7: Tính chu vi hình thoi có cạnh là 5/6 dm

Giải: Chu vi hình thoi là: 5/6 x 4 = 10/3 (dm)

Câu 8: Hình thoi có chu vi bằng 20 cm thì độ dài cạnh của nó bằng bao nhiêu?

Giải: Cạnh của hình thoi là: 20 : 4 = 5 (cm)

Câu 9: Tính độ dài các cạnh của hình thoi ABCD khi biết chu vi hình thoi là 60cm

Giải: Gọi a là độ dài các cạnh của hình thoi. Áp dụng công thức tính chu vi hình thoi, ta có

Chu vi hình thoi ABCD = 4 x a = 60cm

Như vậy, độ dài 1 cạnh của hình thoi là 60/4 = 15 cm

Đáp án: Độ dài một cạnh của hình thoi ABCD là 15 cm

Câu 10: Một sân kho hình thoi đư­ợc mở rộng 2 cạnh về bên phải thêm 3 m , 2 cạnh phía d­ưới thêm 10 m nên trở thành một hình bình hành có chu vi bằng 106 m. Tính cạnh sân kho ban đầu.

Giải: Gọi a là độ dài cạnh của hình thoi

Dựa vào công thức tính chu vi hình bình hành, ta có: P (sân kho) = (a+b) x 2= ((a+3) + (a+10)) x 2 = 106

Giải phương trình trên, ta dễ dàng tìm được cạnh của sân kho ban đầu là 22.5 cm

Đáp án: Chiều dài cạnh sân kho ban đầu là 22.5cm

2. Bài tập tính chu vi hình thoi không có lời giải

Câu 1: Tính chu vi của hình thoi ABCD có độ dài AB = 5cm.

Câu 2: Cho hình thoi ABCD có chu vi bằng 20cm, đường chéo BD = 6cm. Tính độ dài đường chéo AC.

Câu 3: Hai đường chéo của hình thoi có độ dài 6cm và 8cm. Tính chu vi hình thoi đó.

Câu 4: Một hình thoi có độ dài cạnh bằng 20cm. Hỏi chu vi hình thoi đó bằng bao nhiêu?

Câu 5: Tính chu vi hình thoi ABCD khi biết độ dài cạnh là 10cm.

Câu 6: Tính độ dài các cạnh của hình thoi ABCD khi biết chu vi hình thoi là 60cm.

Câu 7: Tính độ dài các cạnh của hình thoi khi biết chu vi hình thoi là 40cm

Câu 8: Hai đường chéo của hình thoi có độ dài 12cm và 20cm. Tính chu vi hình thoi.

Câu 9: Tính chu vi hình thoi ABCD khi biết độ dài cạnh là 14 cm.

Câu 10: Một miếng đất hình thoi có độ dài một cạnh bằng 42m, người ta muốn rào xung quanh miếng đất bằng 4 đường dây kẽm gai. Hỏi cần tất cả bao nhiêu mét dây kẽm gai để rào?

Trên đây là công thức Chu vi hình Thoi & cách tính chu vi hình Thoi đơn giản, nhanh chóng mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể tính được chu vi hình Thoi một cách dễ dàng. Nếu có gì thắc mắc bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc các bạn thành công.