Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo)

Với bài tập Toán lớp 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo), chi tiết này sẽ giúp học sinh có thể dễ dàng xem và so sánh lời giải, từ đó nắm vững cách làm bài tập môn Toán lớp 8.

Bài 5 trong Mục lục Giải Toán 8 là về những hằng đẳng thức đáng nhớ (tiếp theo).

//www.youtube.com/watch?v=0QV_Eddh-zs

Video giải Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo) (P1) đã được cải thiện để mang lại những trải nghiệm sáng tạo hơn.

//www.youtube.com/watch?v=U9abZ32_5Sw

Bài viết này sẽ giới thiệu về một video giải toán ở lớp 8, bài 5 với chủ đề là những hằng đẳng thức đáng nhớ. Đây là phần tiếp theo của video.

Câu hỏi.

Tính biểu thức (a + b)(a2 – ab + b2) trong bài tập số 1 trang 14 sách Toán lớp 8 Tập 1, với a và b là hai số bất kỳ.

Lời giải.

Có thể viết lại đoạn văn như sau: Ta có biểu thức (a + b)(a2 – ab + b2).

A(a^2 – ab + b^2) + b(a^2 – ab + b^2)

A.A2 – a.Ab + a.B2 + b.A2 – b.Ab + b.B2 được viết lại thành a^3 + b^3.

= A^3 – a^2b + ab^2 + ba^2 – b^2a + b^3

= A^3 + (-a^2b + ba^2) + (ab^2 – b^2a) + b^3.

Đầu vào: = a3 + 0 + 0 + b3.Đầu ra: a3 + b3.

Công thức: a3 + b3.

Phát biểu hằng đẳng thức số (6) trang 15 trong sách Toán 8 Tập 1 là câu hỏi như sau:

Lời giải.

Tích của tổng hai biểu thức và bình phương của hiệu hai biểu thức là tổng lập phương của hai biểu thức.

Áp dụng.

Dưới đây là cách viết lại đoạn văn:Input: a) Viết x3 + 8 dưới dạng tích;Biểu diễn x3 + 8 dưới dạng tích là gì?

Đáp án: x^3 + x^2 + x + 1.

Lời giải.

X3 + 8 = x3 + 23.

Biểu thức này hiện đang nằm ở vế trái của một hằng đẳng thức số (6), trong đó A được gán bằng x và B được gán bằng 2.

Sử dụng công thức số học (6), ta có:

Đầu tiên, chúng ta sẽ viết lại đề bài theo một cách sáng tạo hơn:Input: x3 + 8 = x3 + 23 = (x + 2)(x2 – x.2 + 22)Phương trình x3 + 8 = x3 + 23 có thể được biểu diễn dưới dạng (x + 2)(x2 – x.2 + 22).

Đầu vào: = (x + 2)(x2 – 2x + 4).Đầu ra: = (x^2 + 2x + 2)(x^2 – 2x + 4).

Đoạn văn sau khi được viết lại: Cho biểu thức x3 + 8, ta có thể phân tích nó thành (x + 2)(x2 – 2x + 4).

B) Chúng ta có:

(X + 1)(x2 – x + 1) = (x + 1)(x2 – x + 12)

Với A = x và B = 1, biểu thức này hiện đang nằm ở vế phải của hằng đẳng thức số (6).

Sử dụng công thức số học (6), ta có:

(X + 1)(x2 – x + 1) = (x + 1)(x2 – x + 12)

X3 + 13 = x3 + 1.

(X + 1)(x^2 – x + 1) = x^3 + 1

Tính (a – b)(a2 + ab + b2) với a, b là hai số tùy ý.

Lời giải.

Bình phương của a trừ b, nhân với tổng của a bình phương, a nhân b và bình phương của b.

A(a^2 + ab + b^2) – b(a^2 + ab + b^2)

A^3 + a^2b + ab^2 – ba^2 – ab^2 – b^3

= A^3 + (a^2b – ba^2) + (ab^2 – ab^2) – b^3.

= A^3 + 0 + 0 – b^3.

A mũ ba trừ b mũ ba.

(A – b)(a^2 + ab + b^2) = a^3 – b^3

Phát biểu hằng đẳng thức (7) trang 15 Toán 8 Tập 1 là gì?

Lời giải.

Lập phương của hiệu hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó.

Áp dụng.

A) Tính đa thức (x – 1)(x2 + x + 1).

Tích của 8 lần 3 trừ lập phương của y là.

Đánh dấu x vào ô có đáp án đúng của tích: (x + 2)(x² – 2x + 4).

x3 + 8
x3 – 8
(x + 2)3
(x – 2)3

Lời giải.

Biểu thức ban đầu đã cho có dạng vế phải của một hằng đẳng thức với A bằng x và B bằng 1, được biểu diễn như sau:

(X – 1)(x2 + x + 1) = (x – 1)(x2 + x + 12)

Đối với biểu thức x3 – 13, chúng ta có thể viết lại nó thành x3 – 1.

Đoạn văn đã được viết lại: Ta có phương trình (x – 1)(x2 + x + 1) = x3 – 1.

B) Khi so sánh 8×3 – y3 và (2x)3 – y3, chúng ta có:

Khi A = 2x và B = y, biểu thức trên có dạng vế trái của hằng đẳng thức số (7).

(8 nhân 3) trừ y mũ 3 bằng (2 nhân x) mũ 3 trừ y mũ 3.

Kết quả: = (2x – y)(4x^2 + 2xy + y^2)

Đầu vào: = (2x – y)(4×2 + 2xy + y2)Đầu ra: (2x – y)(4x^2 + 2xy + y^2)

(8×3 – y3) có thể được viết lại thành (2x – y)(4×2 + 2xy + y2).

C) Dưới đây là những điều ta có được:

(X + 2)(x^2 – 2x + 4) = (x + 2)(x^2 – 2x + 22)

Trong biểu thức trên, chúng ta có phần vế phải của hằng đẳng thức số (6), trong đó A được gán giá trị là x và B được gán giá trị là 2.

Sử dụng công thức số học (6), ta có:

(X + 2)(x^2 – 2x + 4) = (x + 2)(x^2 – 2x + 22)

= X3 – 23 = x3 – 8.

Dưới đây là bảng mà chúng ta có:

x3 + 8
x3 – 8	x
(x + 2)3
(x – 2)3

Bài tập.

Các biểu thức sau được rút gọn trong bài 30 trang 16 Toán 8 Tập 1.

(X + 3)(x^2 – 3x + 9) – (54 + x^3)

B) (2x + y)(4x^2 – 2xy + y^2) – (2x – y)(4x^2 + 2xy + y^2).

Lời giải:.

Đầu tiên, ta phân tích biểu thức và nhân các đơn thức lại với nhau:(x + 3)(x^2 – 3x + 9) – (54 + x^3)= x(x^2 – 3x + 9) + 3(x^2 – 3x + 9) – (54 + x^3)= x^3 – 3x^2 + 9x + 3x^2 – 9x + 27 – 54 – x^3= -54 + 27= -27Vậy kết quả là -27.

Đầu vào: = (x + 3)(x2 – 3x + 32) – (54 + x3).Kết quả: = (x + 3)(x^2 – 3x + 32) – (54 + x^3).

X3 + 33 – (54 + x3) được viết lại thành 33 – 54.

Áp dụng hình thức toán tử (6) với A là x và B là 3.

= 27 – 54

= -27.

B) (2x + y)(4x^2 – 2xy + y^2) – (2x – y)(4x^2 + 2xy + y^2).

Kết quả: = (2x + y)[4x^2 – 2xy + y^2] – (2x – y)[4x^2 + 2xy + y^2].

[(2x)3 + y3] – [(2x)3 – y3] có thể viết lại là [2x³ + y³] – [2x³ – y³].

Đầu tiên, ta có thể rút gọn biểu thức bằng cách loại bỏ các số mũ giống nhau:(2x)3 + y3 – (2x)3 + y3Sau khi rút gọn, ta được:0 + 2y3Vậy đoạn văn đã được viết lại là:0 + 2y3

= 2y3.

Bài 31 trang 16 của sách Toán 8 Tập 1: Chứng minh rằng:

A) (a + b)3 – 3ab(a + b) = a3 + 3a2b + 3ab2 + b3.

(A – b)3 = a3 – 3a2b + 3ab2 – b3 + 3ab(a – b)

Áp dụng: Tìm giá trị của biểu thức a3 + b3, trong đó a và b là hai số thỏa mãn a.B = 6 và a + b = -5.

Lời giải:.

Biến đổi bên phải ta thu được:

( A + b )3 – 3ab( a + b )

Đoạn văn đã được viết lại: a3 + 3a2b + 3ab2 + b3 – 3a2b – 3ab2.

= A mũ 3 + b mũ 3.

Công thức phát triển của a3 + b3 là (a + b)3 – 3ab(a + b).

B) Ta có thể biến đổi phần vế phải như sau:

(3a – 3b) + 3ab(a – b)

A3 – 3a2b + 3ab2 – b3 + 3a2b – 3ab2

= (A – b)(a^2 + ab + b^2)

(A – b)3 = a3 – 3a2b + 3ab2 – b3 + 3ab(a – b)

Áp dụng vào trường hợp ab = 6 và a + b = -5, ta thu được:

(A + b)3 = a3 + 3a2b + 3ab2 + b3 – 3ab(a + b)

= (-5)^3 – 3.6.(-5) = -125 + 3.6.5.

125 cộng với 90 bằng -35.

Bài 32 trang 16 trong sách Toán 8 Tập 1 yêu cầu học sinh điền các đơn thức thích hợp vào ô trống.

A) 3x+y−+=27×3+y3;.

B) 2x−+10x+=8×3−125.

Lời giải:.

(6) có thể được nhận thấy như một hằng đẳng thức.

3 nhân 27, cộng với y mũ 3.

3 lần bình phương của x, cộng với lập phương của y.

(3x + y)[(3x)^2 – 3xy + y^2]

Khi áp dụng hệ đẳng thức (6) với A = 3x và B = y, chúng ta có:

Đầu vào: = (3x + y)(9×2 – 3xy + y2).Kết quả: = 27×3 – 9x2y + 3xy2 + 9xy2 – 3y3 + y3.

Cần điền gì vào chỗ trống?

3x+y9x2−3xy+y2=27×3+y3.

Ta dễ dàng nhận thấy rằng đây chính là một hằng đẳng thức (7).

125 trừ đi 8 lần 3 bằng một số nào đó.

(2x) mũ 3 trừ 53.

Đầu vào: = (2x – 5).[(2x)2 + (2x).5 + 52].Đầu ra: = (2x – 5)[(2x)2 + (2x)5 + 52].

Áp dụng hệ đẳng thức (7) với A = 2x, B = 5.

(2x – 5) nhân với (4x^2 + 10x + 25) là phép tính được thực hiện.

Cần điền gì vào chỗ trống?

2x−54×2+10x+25=8×3−125.

Toán 8 Tập 1, Bài 33 trang 16:

(2 + xy)2 được viết lại thành b) bình phương của tổng 2 và tích xy.

B) Bình phương của hiệu giữa 5 và tích của 3 và x.

(5 – x2)(5 + x2) được viết lại thành c) (5^2 – x^4)

Đáp án: (5x – 1)³.

(2x – y)(4×2 + 2xy + y2) có thể được viết lại dưới dạng e) 8×3 – 2x2y – 4xy2 – 2y3.

Đầu ra: f) (x + 3)(x^2 – 3x + 9).

Lời giải.

Với đầu vào là a) (2 + xy)2, đầu ra sau khi được viết lại có thể là: b) (2 + xy) dồn bình phương.

= 22 + 2.2.Xy + (xy)2 (dùng hằng đẳng thức số (1))

Đầu tiên, chúng ta có thể viết lại biểu thức đó thành: x^2y^2 + 4xy + 4.

(5 – 3x)2 có thể được viết lại là bình phương của (5 – 3x).

= 52 – 2.5.3x + (3x)² (sử dụng công thức số (2))

Đoạn văn đã được viết lại: Đặt biểu thức là 9x^2 – 30x + 25.

(5 – x2)(5 + x2) có thể được viết lại thành (5^2 – x^4).

Áp dụng hằng đẳng thức số (3), ta có: = 52 – (x^2)^2

= X4 – 25

D) (5x – 1)3 có thể được viết lại là (5x – 1) nhân với chính nó ba lần.

(5x)^3 – 3(5x)^2 + 3(5x)(12) – 13 (áp dụng công thức số học (5))

125 lần 3 trừ 3.25 nhân 2.1 cộng 3.5 lần 0.1 trừ 1.

125 lần 3 trừ 75 lần 2 cộng 15 lần x trừ 1.

(2x – y)(4×2 + 2xy + y2) có thể viết lại thành (2x – y) * (4×2 + 2xy + y2).

Kết quả: = (2x – y)(4x^2 + 2xy + y^2)

(2x)3 – y3 (áp dụng hằng đẳng thức số (7)) được viết lại thành: (2x)3 – y3 = 8×3 – y3.

Đầu vào: = 8×3 – y3.Đầu ra: Phương trình được viết lại thành: 8x^3 – y^3.

F) (x + 3)(x^2 – 3x + 9)

Đầu vào: = (x + 3)(x² – 3x + 32)Đầu ra: (x + 3)(x² – 3x + 32)

Kết quả: 3x + 33 (sử dụng quy tắc số (6)).

Công thức = x^3 + 27.

Các biểu thức cần rút gọn trong bài 34 trang 17 của sách Toán 8 Tập 1 là:

Đầu vào: a) (a + b)2 – (a – b)2;Đầu ra: a² + 2ab + b² – (a² – 2ab + b²);

B) (a + b)3 – (a – b)3 – 2b3; -> Trừ 2b3 khỏi hiệu thức (a + b)3 – (a – b)3.

Đầu tiên, ta có thể viết lại công thức trên dưới dạng khối đa thức:c) (x + y + z)² – 2.(X + y + z).(X + y) + (x + y)²Tiếp theo, ta thực hiện phân tích đa thức:= c.(X + y + z)² – 2.(X + y + z).(X + y) + (x + y)²= c.(X² + 2xy + y² + 2xz + 2yz + z²) – 2.(X² + 2xy + y² + xz + yz) + (x² + 2xy + y²)= cx² + 2cxy + cy² + 2cxz + 2cyz + cz² – 2x² –

Lời giải.

Bình phương của tổng a và b trừ đi bình phương của hiệu a và b.

= 2ab + 2ab

= 2ab + 2ab

= (A^2 – a^2) + (2ab + 2ab) + (b^2 – b^2).

0 + 4ab + 0 có thể được viết lại thành 4ab

= 4ab.

(3(a + b)² – 3(a + b)(a – b) – (a – b)³ – 2b³)

= A^3 + 3a^2b + 3ab^2 + b^3 – (a^3 – 3a^2b + 3ab^2 – b^3) – 2b^3.

Đầu vào: = a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3 – 2b3.Đầu ra: = 2a3 + 6a2b – 2b3.

(A^3 – a^3) + (3a^2b + 3a^2b) + (3ab^2 – 3ab^2) + (b^3 + b^3 – 2b^3).

0 + 6a2b + 0 + 0 = 6a2b

= 6a2b.

Đầu tiên, chúng ta sẽ viết lại công thức \((x + y + z)^2 – 2(x + y + z)(x + y) + (x + y)^2\) bằng cách sử dụng các phép nhân và bình phương:\(c) (x + y + z)^2 – 2(x + y + z)(x + y) + (x + y)^2\)\(= c(x^2 + 2xy + 2xz + y^2 + 2yz + z^2) – 2(x^2 + 2xy + y^2 + xz + yz) + (x^2 + 2xy + y^2)\)\(= cx^2 + 2cxy + 2cxz + cy^2 + 2cyz + cz^2 – 2x^

Khi biểu thức trên có dạng hằng đẳng thức số (2) với A = x + y + z và B = x + y, ta có:

Bình phương của tổng (x + y + z) trừ đi gấp đôi tích (x + y + z) với (x + y) và cộng thêm bình phương của tổng (x + y).

Bình phương của hiệu giữa tổng (x + y + z) và tổng (x + y) là: [(x + y + z) – (x + y)]2.

Bình phương của biểu thức (x + y + z – x – y) là (x + y + z – x – y)2.

[(X – x) + (y – y) + z]2 có thể được viết lại một cách sáng tạo hơn là [0 + 0 + z]2.

= Z2.

Trang 17 của bài 35 trong sách Toán 8 Tập 1 là bài “Tính nhanh”.

A) 342 cộng 662 cộng 68.66.

B) Tổng của 742 và 242 trừ đi 48.74.

Lời giải.

A) 342 cộng 662 cộng 68.66.

342 cộng với 68.66 và 662.

342 cộng với 2,34,66 và 662.

Bình phương của (34 + 66) là bao nhiêu?

= 1002.

10 000. Mười nghìn đồng.

742 cộng 242 trừ 48.74

742 trừ đi 48.74 và cộng thêm 242.

742 trừ 2,24.74 và cộng thêm 242.

Bình phương của hiệu giữa 74 và 24.

= 502.

2 500 là một số lượng lớn.

Trang 17 của bài 36 trong sách Toán 8 Tập 1 đề cập đến việc tính giá trị của một biểu thức.

A) Để tính giá trị của biểu thức x2 + 4x + 4 tại x = 98, ta thực hiện thay x = 98 vào biểu thức và tính toán.

Tại x = 99, công thức b) trở thành: 99^3 + 3(99^2) + 3(99) + 1.

Lời giải:.

Biểu thức x2 + 4x + 4 có thể được viết lại dưới dạng (x + 2)2.

Bình phương của x cộng với 2 lần x nhân với 2, cộng thêm 22.

Đoạn văn đã được viết lại: Hằng đẳng thức số (1) là (x + 2)2.

Khi thay giá trị x = 98 vào biểu thức, ta có: (98 + 2)2 = 1002 = 10 000.

Khi x = 98, giá trị của biểu thức là 10 000.

Đoạn văn đã viết lại: Đa thức bậc ba là x3 + 3×2 + 3x + 1.

X3 + 3×2 + 3×12 + 13

Đầu vào: = (x + 1)3 (Hằng đẳng thức số (4).Đầu ra: Bằng cách nhân (x + 1) với chính nó ba lần, ta có hằng đẳng thức số 4.

Khi thay x = 99 vào biểu thức, ta thu được kết quả là (99 + 1)3 = 1003 = 1 000 000.

Khi x = 99, giá trị của biểu thức là 1 000 000.

Bài 37 trang 17 sách Toán 8 Tập 1 yêu cầu chúng ta sử dụng bút chì để nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức theo mẫu.

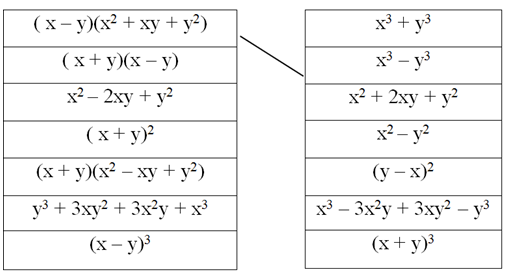
Lời giải.

Ta có:.

Đầu tiên, chúng ta có thể viết lại đoạn văn theo cách sáng tạo hơn như sau: “Khi nhân (x – y) với (x2 + xy + y2), chúng ta sẽ được x3 – y3 (đây là một đẳng thức số có giá trị là 7)”.

Hằng đẳng thức số (3) là (x + y)(x – y) = x2 – y2.

(2) Đẳng thức số: x2 – 2xy + y2 = (x – y)2 = (y – x)2.

Đoạn văn đã được viết lại: Đẳng thức số (1): (x + y)2 = x2 + 2xy + y2.

) Đa thức (x + y) nhân với đa thức (x2 – xy + y2) sẽ cho ra đa thức (x3 + y3) với hằng đẳng thức số là 6.

Y3 + 3xy2 + 3x2y + x3 = (y + x)3 = (x + y)3 (đẳng thức số (4))

) (X – y)3 = x3 – 3x2y + 3xy2 – y3 (đẳng thức số (5)).

Có bảng sau đây:

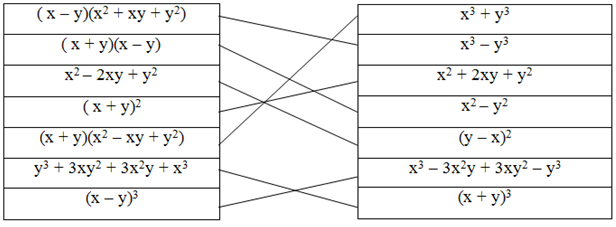
Bài 38 trang 18 sách Toán 8 Tập 1 có nội dung về việc chứng minh các đẳng thức sau đây.

Với a và b là hai số thực bất kỳ, ta có thể viết lại biểu thức (a – b)^3 = -(b – a)^3.

B) Bình phương của hiệu của số âm a và b bằng bình phương của tổng của a và b.

Lời giải:.

(A – b)3 = a3 – 3a2b + 3ab2 – b3

(B – a)3 = – ( b3 – 3b2a + 3ba2 – a3) được viết lại thành: Kết quả của phép nhân (b – a) lũy thừa 3 là âm đẳng với kết quả của phép tính -( b3 – 3b2a + 3ba2 – a3).

Đầu vào: = -b3 + 3ab2 – 3a2b + a3.Đầu ra: a3 – 3a2b + 3ab2 – b3.

= A^3 – 3a^2b + 3ab^2 – b^3.

(A – b)­3 = – (b – a)3, vậy.

B) Cho ta biết: (-a – b)2 = (-a)2 – 2.(-A).B + b2.

Bình phương của a cộng với gấp đôi tích của a và b cộng với bình phương của b bằng bình phương của tổng a và b.

Kết quả: Vì vậy, bình phương của (-a – b) bằng lập phương của (a + b).

//www.youtube.com/watch?v=JWn-ZHt_nBU

Bài học Toán 8 Bài 5 tiếp tục với những hằng đẳng thức đáng nhớ.

Bạn có thể tìm hiểu thêm về lời giải bài tập Toán học lớp 8 bằng cách xem thông tin chi tiết ở đây.

Bài 6: Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.

Phương pháp phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức được trình bày trong Bài 7.

Bài 8: Giải phân tích một đa thức thành nhân tử bằng phương pháp nhóm hạng tử.

Bài 9: Phối hợp nhiều phương pháp để phân tích đa thức thành nhân tử.

Bài 10: Phân chia đơn thức cho đơn thức.

Hãy tham khảo một số tài liệu khác về Toán học lớp 8 để có thông tin chi tiết hơn.

Tiếp tục với lý thuyết Những hằng đẳng thức đáng nhớ.

Đáp án của trắc nghiệm Những hằng đẳng thức đáng nhớ (tiếp theo p2) được cung cấp dưới đây.