1. Định nghĩa về hình tròn.

Đường tròn (O; R) là một hình được tạo thành từ các điểm nằm cách điểm O một khoảng R, với R là bán kính lớn hơn 0.

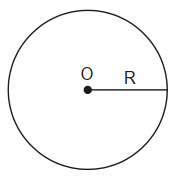
Điểm A thuộc đường tròn (O; R) khi và chỉ khi OA có độ dài bằng R.

Điểm A thuộc đường tròn (O; R) khi và chỉ khi khoảng cách OA nhỏ hơn R.

Điểm A thuộc bên ngoài đường tròn (O; R) khi và chỉ khi OA lớn hơn R.

Bổ sung tri thức:

Đường tròn đi qua các điểm A1, A2, …, An được gọi là đường tròn ngoại tiếp của đa giác A1A2…An.

Đường tròn tiếp xúc với tất cả các cạnh của đa giác A1A2…An được gọi là đường tròn nội tiếp của đa giác đó.

Ví dụ 1: Xác định vị trí các điểm A, B, C đối với đường tròn (O; 5 cm) khi biết độ dài OA = 5 cm, OB = 3 cm, OC = 8 cm.

Lời giải:.

Ta có:.

OA = 5 cm nên điểm A nằm trên vòng tròn (O; 5 cm).

OB = 3 cm < 5 cm do đó điểm B nằm bên trong đường tròn (O; 5 cm).

Vì OC = 8 cm lớn hơn 5 cm, nên điểm C không thuộc đường tròn có tâm là O và bán kính là 5 cm.

Chúng ta có một bức tranh.

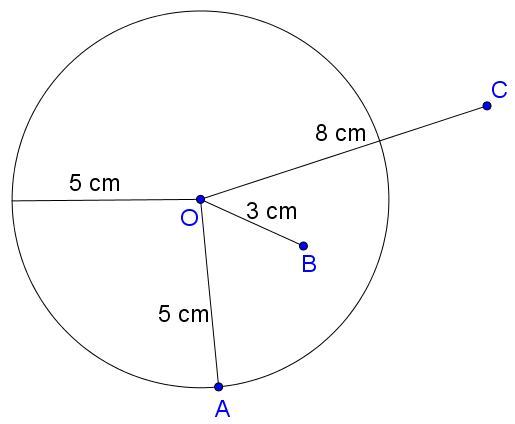
Điểm A được đặt trên đường tròn (O), còn điểm B được đặt bên trong đường tròn (O) và điểm C nằm bên ngoài đường tròn (O).

2. Phương pháp xác định hình tròn.

Qua ba điểm không nằm trên cùng một đường thẳng, chúng ta có thể vẽ được một và chỉ một hình tròn.

Chú ý: Không thể vẽ được hình tròn nào đi qua 3 điểm thẳng nằm trên một đường thẳng.

• Trong tam giác vuông: tâm đường tròn bên ngoài chính là điểm giữa của cạnh huyền.

• Trong tam giác đều: trọng tâm tam giác là tâm đường tròn ngoại tiếp của nó.

• Trong tam giác thường:

Tâm đường tròn ngoại tiếp là điểm chung của ba đường trung trực của ba cạnh tam giác đó.

Tâm đường tròn nội tiếp là điểm chung của ba đường phân giác trong của tam giác đó.

Ví dụ 1.

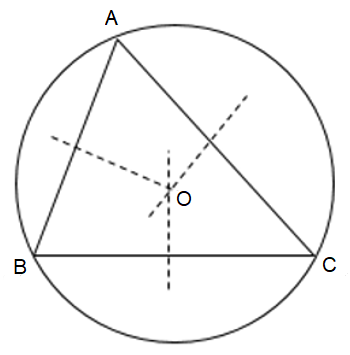
Ba đường trung trực của ba cạnh của tam giác ABC giao nhau tại điểm O.

Khi đó, O là trung tâm đường tròn ngoại tiếp tam giác ABC.

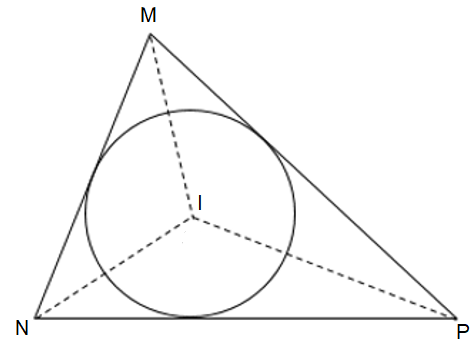
Ba đường chia đều ba cạnh của tam giác MNP giao nhau tại điểm I.

Khi đó, I là trung tâm đường tròn nội tiếp tam giác ∆MNP.

3. Tâm đối xứng.

Hình tròn là một hình có tâm đối xứng. Tâm của hình tròn là tâm đối xứng của hình tròn đó.

Ví dụ 2. Giả sử có đường tròn (O) và điểm A nằm trên đường tròn đó. Ta vẽ điểm A’ là điểm đối xứng với điểm A qua tâm O. Chúng ta cần chứng minh rằng điểm A’ cũng nằm trên đường tròn (O).

Lời giải:.

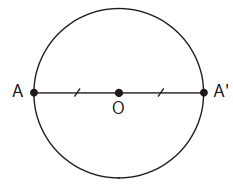
Vì A’ đối xứng với A qua O, nên O được coi là trung điểm của đoạn thẳng AA’.

Lúc đó, OA = OA’ = R.

Vì vậy, điểm A’ nằm trên vòng tròn (O).

Vậy điểm A’ cũng nằm trên đường tròn (O).

4. Trục đối xứng.

Đường tròn có tính chất là hình có trục đối xứng. Mọi đường kính của đường tròn đều là trục đối xứng của nó.

Ví dụ 3. Xét đường tròn (O) có đường kính là AB và điểm M thuộc đường tròn (O). Tìm điểm N đối xứng với điểm M qua đường thẳng AB.

Lúc đó, điểm N cũng nằm trên đường tròn (O).