Góc là gì? Thế nào là góc vuông, góc nhọn, góc tù, góc bẹt?

Góc được hiểu như thế nào? Góc trong tiếng Anh được gọi là gì? Góc vuông, góc nhọn, góc tù và góc bẹt có ý nghĩa ra sao? Có lời giải cho bài tập về tính toán góc không?

Trong lĩnh vực toán học hình học, mặc dù có nhiều loại hình dạng khác nhau, nhưng chúng đều có một điểm chung là có góc. Tùy thuộc vào từng loại hình, cách tính toán, xác định và nhận dạng góc cũng sẽ khác nhau. Có một số loại hình cụ thể và thường được sử dụng như hình vuông, hình chữ nhật và hình tam giác, với các loại góc như góc vuông, góc nhọn, góc tù. Vậy để hiểu rõ hơn về khái niệm góc, góc vuông, góc nhọn, góc tù và góc bẹt, hãy cùng tìm hiểu chi tiết trong bài viết dưới đây.

Tư vấn pháp lý trực tuyến miễn phí qua hotline: 1900.6568.

Góc là một hình được tạo thành bởi hai tia có chung một gốc. Đỉnh của góc chính là điểm chung của hai tia. Hai tia đó cũng là hai cạnh của góc.

Lưu ý:.

Khi hai đường thẳng song song không cắt nhau tại bất kỳ điểm nào, góc giữa của chúng bằng 0 và không có đỉnh xác định.

Đơn vị đo lường của góc là góc đo.

+ Radian:.

Đo bằng Radian là đơn vị đo góc phẳng phổ biến nhất và là đơn vị chuẩn trong toán học. Radian không có đại lượng độc lập cụ thể, mà nó là tỷ lệ giữa độ dài cung tròn và độ dài bán kính.

Đơn vị đo góc Radian.

Trong hệ đo lường quốc tế, góc được đo bằng radian.

Độ là một đơn vị đo lường phổ biến.

Độ được đại diện bằng kí hiệu °.

Đơn vị đo lường Cường độ.

Lưu ý:. Ngoài ra độ còn được chia thành các đơn vị thấp hơn là phút và giây.

Một độ tương đương với 60 phút. Được ký hiệu là “.”

1 phút = 60 giây. Kí hiệu là “.”

Tính chất của góc:

Một tia cũng là một góc và có góc đo là 0°.

Nếu tia OA nằm giữa Oz và Oy thì A nằm ở góc zOy..

A nằm ở góc zOy.

Nếu tia Oa nằm giữa Ox và Oy thì: góc xOa + góc aOy = góc xOy.

Tia phân giác của góc xOy khi:Output: – Tia chia đôi góc xOy khi:

Oa nằm giữa Ox và Oy (góc xOa + góc aOy = góc xOy).

Hai góc được phân chia bởi tia có cùng độ lớn (góc xOa = góc aOy).

Tia chia góc giữa trục xOy.

– Hai góc kề nhau là hai góc có cạnh chung, hai cạnh còn lại nằm trên nửa mặt phẳng đối nhau.

Hai góc tương phụ nhau có tổng độ bằng một góc vuông.

Hai góc khác nhau nhưng có tổng giá trị đo bằng một góc vuông.

Hai góc kề đối là hai góc liền kề và có tổng độ đo bằng 1 góc tù.

Hai tia đối diện tạo thành một góc nghiêng.

Lưu ý:. Các đường thẳng đồng quy tại 1 điểm sẽ tạo ra các cặp 2 góc đối đỉnh nhau và 2 góc này sẽ có cùng số đo.

2. Góc tiếng Anh là gì?

Góc tiếng Anh được gọi là “corner”.

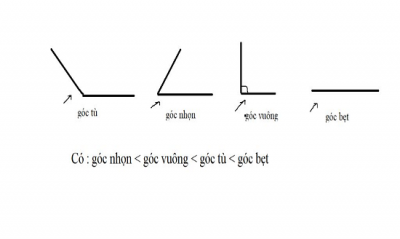
3. Thế nào là góc vuông, góc nhọn, góc tù, góc bẹt:

3.1. Góc nhọn:

Góc nhọn được hình thành bởi sự cắt nhau của hai đường thẳng tại một điểm gọi là giao điểm. Góc có giá trị từ 0° đến 90°.

Trong lĩnh vực toán học hình học, chúng ta thường đề cập đến khái niệm “góc nhọn” để chỉ một góc được tạo thành từ hai đường thẳng có một điểm chung trong mặt phẳng hoặc từ hai cạnh của một tam giác bất kỳ. Góc nhọn có giá trị nhỏ hơn 90° và nằm trong khoảng từ 0 đến 90°. Để xác định chính xác giá trị của một góc nhọn trong hình học, bạn có thể sử dụng công cụ như eke. Cần lưu ý rằng góc nhọn luôn nhỏ hơn góc vuông.

3.2. Góc vuông:

Góc vuông là một góc mà ai cũng có thể nhận ra ngay. Đây là loại góc được sử dụng và tính toán nhiều nhất trong hình học phẳng với giá trị là 90°. Các hình học khác nhau cũng có góc vuông như hình thang, hình chữ nhật, hình tam giác, hình vuông và hình thoi. Tính chất của góc vuông có ý nghĩa và ứng dụng quan trọng trong hình học, giúp giải quyết nhiều bài tập về lượng giác khác nhau.

Góc vuông là góc có độ góc là 90°.

Trong lĩnh vực toán học, chúng ta thường gặp phải khái niệm “góc tù”. Đây là một loại góc đặc biệt được tạo ra từ hai đường thẳng trên mặt phẳng. Góc tù có giá trị lớn hơn góc vuông và nhỏ hơn tổng của ba góc trong một tam giác. Không có hình học phẳng nào có thể tồn tại góc tù.

3.3. Góc tù:

Góc tù được hình thành bởi hai đường thẳng cắt nhau tại một điểm. Đặc điểm của góc tù là có độ lớn góc nằm trong khoảng từ 90° đến 180°.

3.3. Góc bẹt:

Góc bẹt là góc có độ lớn 180°, tức là nửa vòng tròn được tạo ra bởi hai đường thẳng có một điểm chung.

4. Cách xác định giá trị các góc:

Có nhiều phương pháp để xác định giá trị của một góc, phụ thuộc vào loại hình học. Dưới đây là một số cách cơ bản:

Tận dụng đặc điểm của hình học.

Cách xác định giá trị góc của các hình học khác nhau có thể dựa trên tính chất của chúng. Ví dụ, trong hình vuông và hình chữ nhật, giá trị góc luôn là 90°. Trong tam giác, tổng 3 góc luôn bằng 180°. Tuy nhiên, giá trị góc còn lại có thể được suy ra dựa trên các giả thiết hoặc điều kiện của bài tập.

Sử dụng thước đo góc hoặc thước kẻ.

Để xác định các góc, có một phương pháp phổ biến là sử dụng các công cụ đo góc. Những công cụ này giúp xác định chính xác giá trị của một góc. Thông thường, thước đo góc có hình dạng giống một chiếc quạt hoặc một hình tròn. Khoảng giá trị của nó nằm trong khoảng từ 0° đến 180°.

5. Bài tập vận dụng về tính toán góc có lời giải:

Bài 1: Điền vào khoảng trống trong những câu sau đây:.

A, Góc DEF có đỉnh là …. Có hai cạnh là ….

B, Hình bao gồm hai tia cùng xuất phát từ điểm Oa, Ob là …..

Điểm O là … Hai tia Oa, Ob là …..

Góc nghiêng là …..

Khi hai tia Ot và Ov không trùng nhau, điểm A được coi là nằm trong góc tOv nếu tia …. Nằm giữa hai tia ….

Bài 2: Đọc danh sách và biểu tượng các góc trong hình vẽ dưới đây. Trên hình vẽ có bao nhiêu góc?

Bài 3: Đếm số góc có trong các hình vẽ dưới đây:.

Bài số 4: Đặt tên và biểu diễn các góc có trong hình sau đây:

Bài 5: Trong góc bẹt xOy, có ba tia Om, On, Op nằm trên cùng một nửa mặt phẳng với bờ là đường thẳng xy. Hình vẽ có bao nhiêu góc đỉnh O?

Bài 6: Gọi O là điểm chung của 3 đường thẳng xy, zt, uv.

A, Có bao nhiêu góc nghiêng tại đỉnh O, kể tên các góc đó?

Kể tên tất cả các góc có chung đỉnh OD?

Bài 7: Trong một tam giác ABC, có 3 điểm A, B, C không thẳng hàng. Một điểm M được biết là nằm trong cả góc BAC và góc ABC. Liệu M có nằm trong góc BCA hay không?

Bài 8: Giả sử góc xOy không phẳng và tia Oz nằm trong góc đó, trong khi tia Ot nằm trong góc xOz. Chứng minh rằng:

A) Tia Ot nằm trong góc xOy.

B) Tia Oz nằm trong góc yOt.

Bài 9: Trên đường thẳng d, có n điểm (n thuộc N, n > 2) và điểm O không nằm trên đường thẳng đó. Hãy vẽ các tia gốc O đi qua mỗi điểm đã cho. Có bao nhiêu góc đỉnh O mà các cạnh là các tia đã vẽ?

Bài 10: Vẽ một số tia có điểm gốc chung. Biết rằng có tất cả 55 góc. Hỏi có bao nhiêu tia?

C. Đáp án.

Bài 1:.

A, Góc DEF có đỉnh là E có hai cạnh là ED, EF.

B, Hình bao gồm hai tia chung gốc Oa, Ob được gọi là góc aOb.

Điểm O là đỉnh. Hai tia Oa, Ob là hai cạnh của góc.

Góc bẹt là góc có hai cạnh là hai tia đối diện.

Khi hai tia Ot và Ov không trùng nhau, điểm A được coi là nằm trong góc tOv nếu tia OA nằm giữa hai tia Ot và Ov.

Bài 2: Dựa vào hình vẽ ta có các góc xOy, xOz, yOz và trong hình vẽ có tất cả 3 góc.

Bài 3: Hình 1 có sáu góc, hình 2 cũng có sáu góc.

Bài 4:.

Các góc mà hình vẽ chứa là:

Bài 5:.

Có 10 góc đỉnh O, đó là các góc:.

Bài 6:.

A, Có 3 góc nghiêng đỉnh O là các góc: xOy, zOt, uOv.

Có một số góc có chung đỉnh O, bao gồm: xOz, xOu, xOy, xOt, xOv, zOu, zOy, zOt, zOv, uOt, uOv, yOt, yOv, tOv, và uOy.

Bài 7:.

Điểm M nằm trong góc BAC, tia AM cắt đoạn thẳng BC tại điểm H, nằm giữa BC. Điểm A thuộc cạnh BA, điểm H thuộc cạnh BC của góc ABC. Vì M nằm trong góc ABC, tia BM cắt đoạn thẳng AH tại điểm M, nằm giữa A và H. Vì A trên cạnh CA và H trên cạnh CB của góc BCA, tia CM cắt đoạn thẳng AH tại điểm M nằm giữa A và H, nên tia CM nằm giữa 2 tia CB và CA. Do đó, M nằm trong góc BAC.

Bài 8:.

A) Lấy A nằm trên trục Ox, lấy B nằm trên trục Oy, AB giao Oz tại C.

C nằm giữa 2 điểm A và B vì Oz nằm trong góc xOy.

Do Ot nằm trong góc xOz, đoạn thẳng AC cắt tia Ot tại D, với D nằm giữa hai điểm A và C. Vì C nằm giữa A và B, D nằm giữa A và C, suy ra điểm D cũng nằm giữa A và B. Như vậy, ta có Ot nằm trong góc xOy.

Vì điểm A và B nằm ở hai phía đối diện với điểm C, và điểm A và D nằm cùng phía đối diện với điểm C, nên điểm B và D nằm ở hai phía khác nhau so với điểm C. Hoặc có thể nói, điểm C nằm giữa hai điểm B và D. Do đó, ta có thể kết luận rằng tia Oz nằm trong góc yOt.

Bài 9:.

Từ một tia bất kỳ kết hợp với n-1 tia còn lại, ta có thể tạo ra n-1 góc đỉnh O với n tia. Tổng số góc O có các cạnh là các tia đó là n(n-1).

Tuy nhiên, mỗi góc đã được tính toán hai lần.

Do vậy số lượng góc đỉnh O có là n(n-1)/2 góc.

Bài 10:.

Gọi n là số tia. Ta có: n(n-1):2 = 55.

N(n-1) = 110 = 11.10.

N = mười một.

Vậy có tổng cộng 11 tia.

Đây là các thông tin liên quan về nội dung góc và các loại góc cũng như cách xác định và tính toán các góc trong toán học. Đây không chỉ là cách xác định trên lý thuyết mà còn có thể áp dụng vào thực tế trong việc đo đạc tính toán các số liệu về thiết kế hay ứng dụng khác. Để làm được điều đó, cần phải có những kiến thức chung để xác định một cách chính xác nhất.