Hình thang là một trong những kiến thức Toán học quan trọng đối với các bạn học sinh lớp 4, lớp 5, lớp 6 và gặp lại nhiều ở năm lớp 8. Vậy hình thang là gì và cách tính chu vi của nó ra sao?

Sau đây, đội ngũ INVERT chúng tôi sẽ hướng dẫn bạn cách tính diện tích hình thang vô cùng đơn giản, chi tiết, dễ hiểu thông qua bài viết sau.

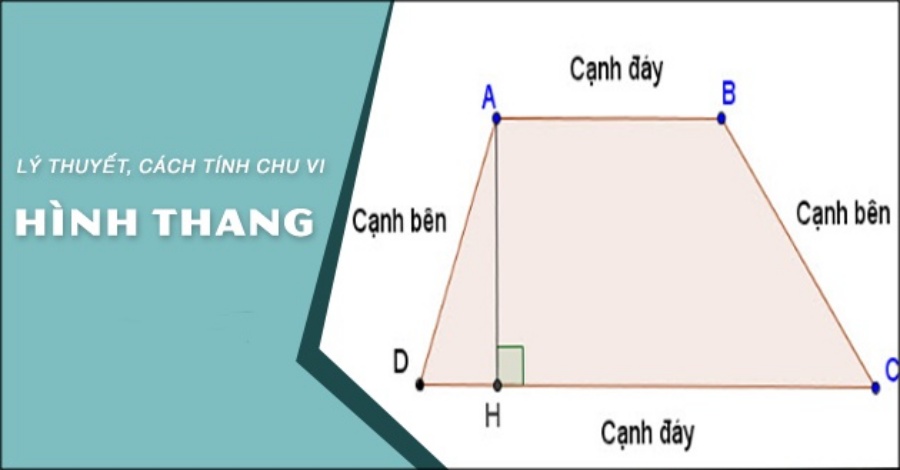
I. Hình thang là gì? Chu vi hình thang là gì?

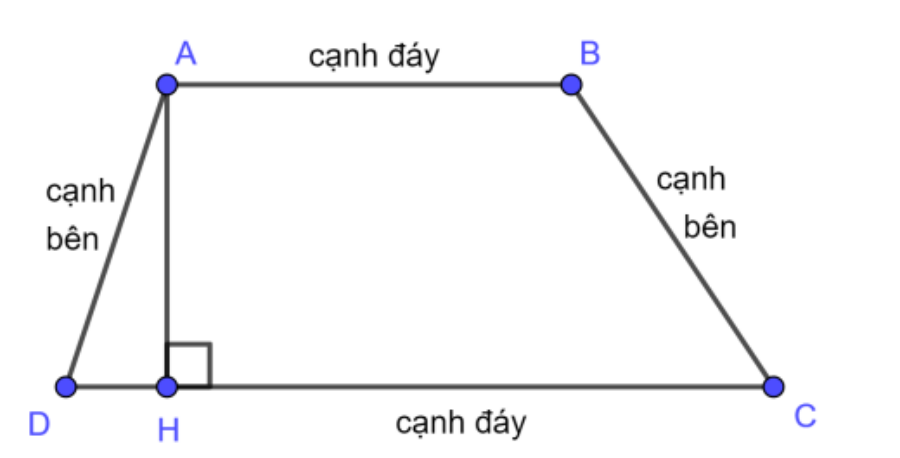
Hình thang trong hình học Euclide là 1 tứ giác lồi có 2 cạnh đối song song. Bên cạnh đó, 2 cạnh song song này được gọi là các cạnh đáy của hình thang và 2 cạnh còn lại gọi là 2 cạnh bên.

Chu vi hình thang là tổng độ dài của cạnh đáy và 2 cạnh bên của hình thang

Các dạng đặc biệt của hình thang:

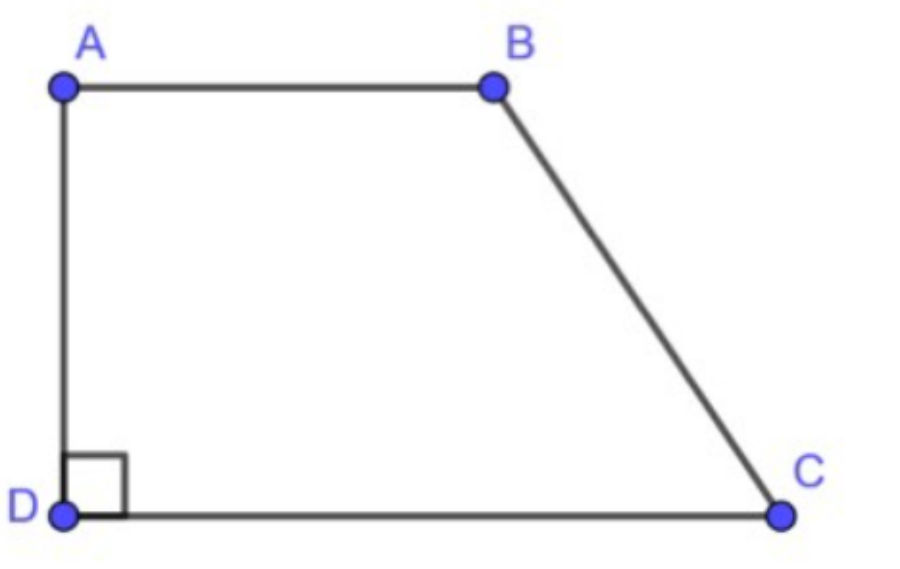
• Hình thang vuông là hình thang có 1 góc vuông.

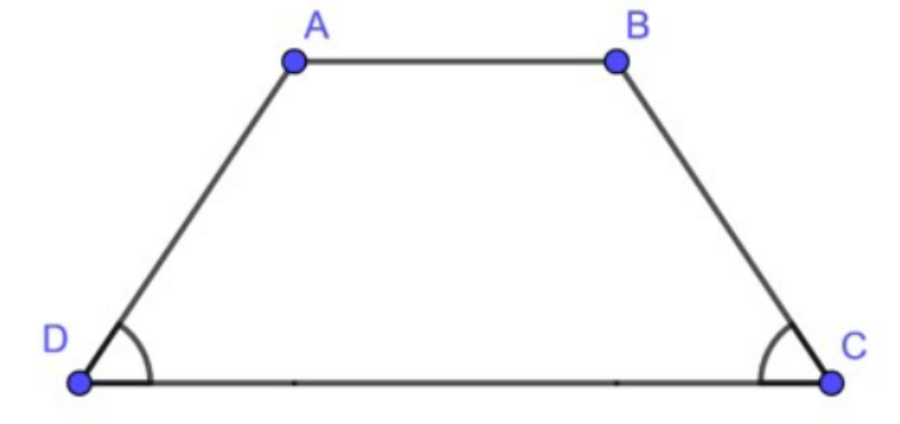
• Hình thang cân là hình thang có 2 góc kề 1 đáy bằng nhau.

• Hình bình hành là hình thang có 2 cạnh đáy bằng nhau và 2 cạnh bên song song và bằng nhau.

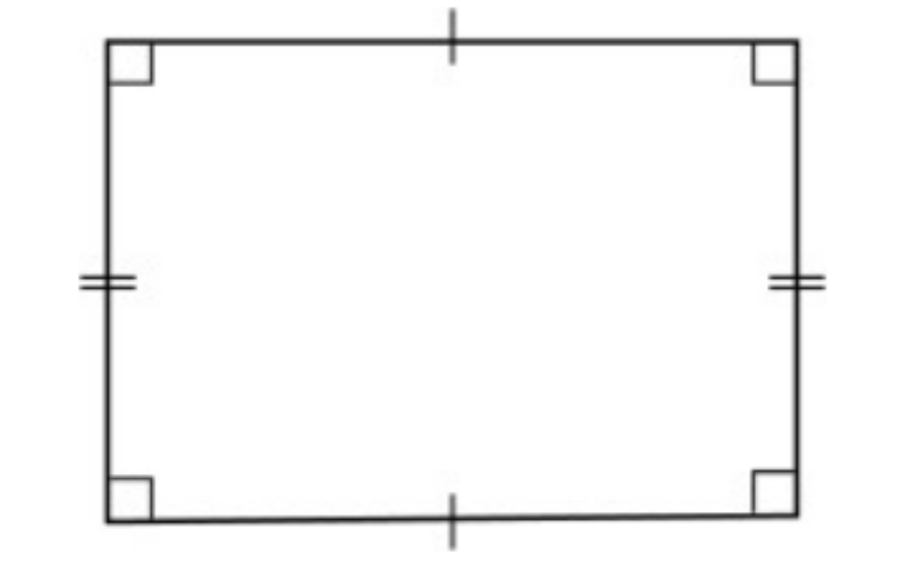
• Hình chữ nhật là hình thang vừa vuông vừa cân.

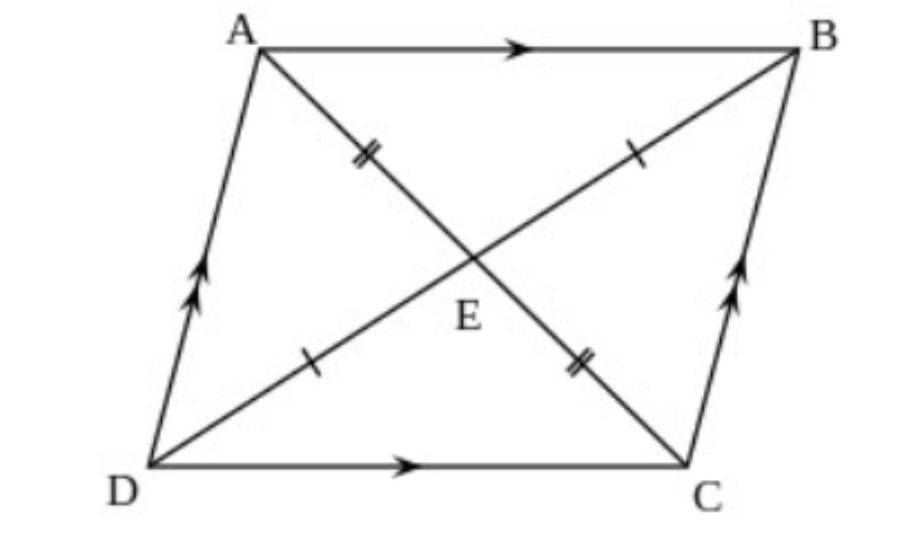
Tính chất của hình thang:

– Tính chất về góc

• Hai góc kề 1 cạnh bên của hình thang có tổng bằng 180° (2 góc nằm ở vị trí trong cùng phía của 2 đoạn thẳng song song là 2 cạnh đáy).
• Trong hình thang cân, 2 góc kề 1 đáy bằng nhau.

– Tính chất về cạnh

• Hình thang có 2 cạnh đáy bằng nhau thì 2 cạnh bên song song và bằng nhau
• Ngược lại, nếu hình thang có 2 cạnh bên song song thì chúng bằng nhau và 2 cạnh đáy cũng bằng nhau
• Trong hình thang cân, 2 đường chéo bằng nhau.

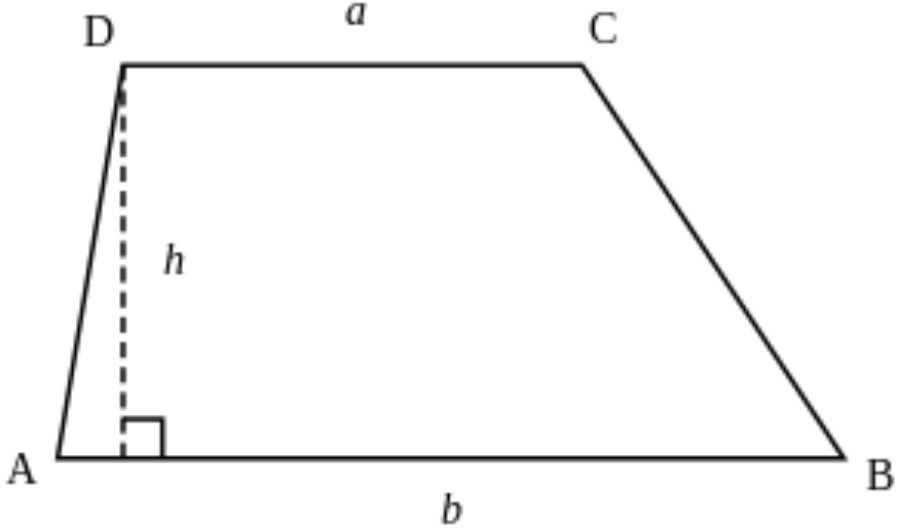
II. Công thức tính chu vi hình thang

Chu vi hình thang được tính bằng độ dài các cạnh hình thang cộng lại với nhau.

Công thức tổng quát:

Trong đó:

• C: Chu vi hình thang
• a, b: Hai cạnh đáy hình thang.
• c, d: Hai cạnh bên hình thang.

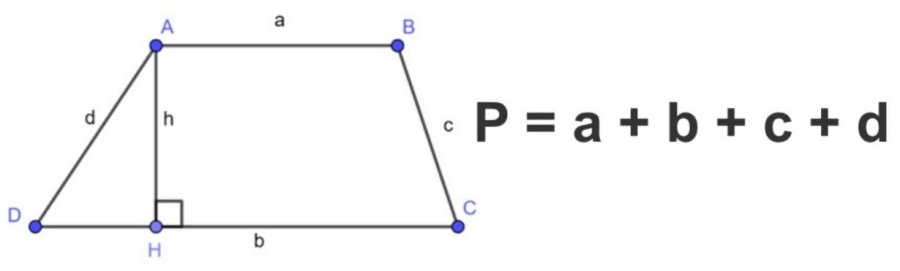
Mở rộng: Nếu biết chu vi hình thang và độ dài 3 cạnh, ta có thể tìm cạnh còn lại bằng cách lấy chu vi trừ đi tổng độ dài 3 cạnh: a = C – (b + c + d).

Hình thang vuông có cách tính chu vi tương tự hình thang thường.

Công thức:

Trong đó:

• C: Chu vi hình thang
• a, b: Hai cạnh đáy hình thang.
• c, d: Hai cạnh bên hình thang.

Chu vi hình thang cân được tính bằng 2 nhân với độ dài cạnh bên sau đó cộng với độ dài của 2 cạnh đáy.

Trong đó:

• C: Chu vi hình thang
• a: Cạnh bên hình thang.
• b, c: Hai cạnh đáy hình thang.

III. Dấu hiệu nhận biết hình thang

– Hình thang có 5 dấu hiệu nhận biết như sau:

+ Tứ giác có 2 cạnh đối song song

+ Hình thang có 1 góc vuông là hình thang vuông

+ Hình thang có 2 góc kề một đáy là hình thang cân

+ Hình thang có 2 cạnh bên bằng nhau là hình thang cân

+ Hình thang có 2 đường chéo bằng nhau là hình thang cân

– Dấu hiệu nhận biết hình thang cân:

+ Hình thang có 2 góc kề 1 cạnh đáy bằng nhau.

+ Hình thang có 2 đường chéo bằng nhau.

+ Hình thang có 2 trục đối xứng của hai đáy trùng nhau.

+ Hình thang có 2 cạnh bên bằng nhau.

+ Hình thang nội tiếp đường tròn.

IV. Một số bài tập tính chu vi hình thang

1. Bài tập tính chu vi hình thang có lời giải

Câu 1: Tính chu vi của hình thang, biết:

a) Đáy lớn = 12 cm; đáy bé = 10 cm; hai cạnh bên lần lượt = 7 cm và 8 cm

b) Đáy lớn = 10,3 dm; đáy bé = 7,8 dm; hai cạnh bên lần lượt = 4,5 dm và 6 dm.

c) Đáy lớn = 7 m, đáy bé = 5 m; hai cạnh bên lần lượt = 3 m và 4 m

d) Đáy lớn = 8 cm; đáy bé bằng 1⁄2 đáy lớn; hai cạnh bên lần lượt = 6 cm và 7 cm

Giải:

a) Chu vi của hình thang là: 12 + 10 + 7 + 8 = 37 (cm)

b) Chu vi của hình thang là: 10,3 + 7,8 + 4,5 + 6 = 28,6 (dm)

c) Chu vi của hình thang là: 7 + 5 + 3 + 4 = 19 (m)

d) Đáy bé hình thang là: 8 : 2 = 4 (cm)

Chu vi hình thang là: 8 + 4 + 6 + 7 = 25 (cm)

Câu 2: Tính độ dài của hình thang có hai cạnh bên bằng nhau biết chu vi của hình thang bằng 68cm và độ dài hai cạnh đáy lần lượt là 20cm và 26cm. Tính chiều dài cạnh bên của hình thang

Giải:

Tổng độ dài hai cạnh bên của hình thang là: 68 – 20 – 26 = 22 (cm)

Độ dài cạnh bên của hình thang là: 22 : 2 = 11 (cm)

Đáp số: 11cm

Câu 3: Tính chu vi hình thang biết độ dài 2 đáy và 2 cạnh bên lần lượt bằng: 3cm, 6cm, 4cm, 5cm.

Giải:

Chu vi của hình thang là: 3 + 6 + 4 + 5 = 18 (cm). Đáp số: 18 cm

Câu 4: Một mảnh vườn trồng táo hình thang có đáy lớn bằng 30m, đáy bé bằng nửa đáy lớn. Độ dài cạnh bên thứ nhất của mảnh vườn là 15m, độ dài cạnh bên thứ 2 gấp 3 lần độ dài cạnh bên thứ nhất. Tính chu vi mảnh vườn đó ?

Giải:

Độ dài đáy bé là : 30 : 2 = 15 ( m )

Độ dài cạnh bên thứ hai là : 15 x 3 = 45 ( m )

Chu vi mảnh vườn đó là : P = a + b + c + d = 30 + 15 +15 + 45 = 105 ( m )

Câu 5: Tính chu vi của hình thang biết độ dài 2 đáy và 2 cạnh bên lần lượt bằng: 2cm, 5cm, 3cm, 2cm.

Giải:

Chu vi của hình thang là:

C = 2 + 5 + 3 + 2 = 12cm

Đáp số: 12cm

Câu 6: Cho hình thang vuông ABCD với chiều dài cạnh góc vuông là 10 cm, chiều dài cạnh còn là là 12 cm. Biết chu vi hình thang là 100cm2, đáy lớn gấp đôi đáy nhỏ. Tính chiều dài các đáy trong hình thang này.

Giải:

Chu vi hình thang vuông: P = 12 + 10 + 3 x (đáy nhỏ) = 100 cm

Khi đó, chiều dài đáy nhỏ của hình thang là : (100 – 12-10)/3 = 26 cm

Chiều dài đáy lớn của hình thang là: 26 x 2 = 52 cm

Đáp án: Chiều dài đáy nhỏ của hình thang là 26cm, chiều dài đáy lớn của hình thang là 52 cm

Câu 7: Tính chu vi hình thang biết đáy lớn bằng 14cm, đáy bé bằng 10cm, 2 cạnh bên lần lượt bằng 6cm, và 8cm.

Giải:

Chu vi hình thang là:

C = 14 + 10 + 6 + 8 = 38cm

Đáp số: 38cm

Câu 8: Tính chu vi hình thang biết đáy lớn bằng 26cm, đáy bé bằng ½ đáy lớn, và 2 cạnh bên có diện tích lần lượt là 22cm, 24cm.

Giải:

Đáy bé hình thang là 26 : 2 = 13cm

Chu vi hình thang là: 26 + 13 + 22 + 24 = 85cm

Câu 9: Tìm chu vi hình thang cân ABCD biết đáy lớn bằng 8cm, đáy nhỏ bằng 3cm và cạnh bên bằng 5cm.

Giải:

Chu vi hình thang cân ABCD là:

P = 8 + 3 + 2.5 = 21(cm)

Đáp số: 21cm

Câu 10: Tính chu vi của hình thang cân biết 1 góc bằng 60° và 2 đáy có độ dài 15 cm và 49 cm

Giải:

Giả sử: Hình thang cân ABCD có đáy nhỏ là AB, đáy lớn CD

Góc ADC = 60°

Từ A kẻ đường vuông góc xuống DC cắt DC tại H

⇒ DH = (49 – 15)/2 = 17

Cos góc ADC = cos60 = DH/AD = 1/2

⇒ AD = 34

⇒ Chu vi hình thang cân ABCD là: 15 + 49 + 34 + 34 = 132 (cm)

2. Bài tập tính chu vi hình thang không có lời giải

Câu 1: Cho hình thang có hai cạnh đáy lần lượt là 6cm và 4cm. Chiều dài của cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó, biết rằng hình thang có hai cạnh bên bằng nhau?

Câu 2: Tính chu vi các hình thang có độ dài đáy lớn và đáy bé lần lượt là a và b:

a) a = 14cm; b = 6cm

b) a =23m; b = 12m

c) a = 2,8m; b = 1,8m

Câu 3: Cho hình thang ABCD có AB = 4, BC = 6, CD = 5, DA = 3. Tính chu vi hình thang ABCD

Câu 4: Cho hình thang ABCD có AB = 2, BC = 3, CD = 6.5 và góc ADC = góc BCD. Tính chu vi hình thang ABCD.

Câu 5: Tính độ dài của hình thang có hai cạnh bên bằng nhau biết chu vi của hình thang bằng 48cm và độ dài hai cạnh đáy lần lượt là 12cm và 24cm. Tính chiều dài cạnh bên của hình thang

Câu 6: Tìm chu vi hình thang cân ABCD biết đáy lớn bằng 10cm, đáy nhỏ bằng 6cm và cạnh bên bằng 5cm.

Câu 7: Tính chu vi của hình thang cân biết 1 góc bằng 30° và 2 đáy có độ dài 13 cm và 42 cm

Câu 8: Tính chu vi hình thang biết đáy lớn bằng 56cm, đáy bé bằng ½ đáy lớn, và 2 cạnh bên có diện tích lần lượt là 32cm, 22cm.

Câu 9: Tính chu vi của hình thang cân biết 1 góc bằng 60° và 2 đáy có độ dài 7 cm và 15 cm

Câu 10: Tìm chu vi hình thang cân ABCD biết đáy lớn bằng 18cm, đáy nhỏ bằng 6cm và cạnh bên bằng 5cm.

Trên đây là công thức Chu vi hình Thang & cách tính chu vi hình Thang đơn giản, nhanh chóng mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể tính được chu vi hình Thang một cách dễ dàng. Nếu có gì thắc mắc bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc các bạn thành công.