Bây giờ khi chúng ta biết thế nào là tam giác vuông và các tam giác vuông đặc biệt là gì, đây là thời điểm thích hợp để thảo luận về từng loại trong số chúng. Hãy xem tam giác 45 ° -45 ° -90 ° là gì?

Tam giác 45 ° -45 ° -90 ° là gì?

Tam giác 45 ° -45 ° -90 ° là một tam giác vuông đặc biệt có hai góc 45 độ và một góc 90 độ. Độ dài các cạnh của tam giác này theo tỷ lệ;

Mặt 1: Mặt 2: Hypotenuse = n: n: n√2 = 1: 1: √2.

Hình tam giác vuông 45 ° -45 ° -90 ° là một nửa của hình vuông . Điều này là do hình vuông có mỗi góc bằng 90 °, và khi nó bị cắt theo đường chéo, một góc vẫn là 90 ° và hai góc 90 ° còn lại bị chia đôi (cắt thành một nửa) và mỗi góc trở thành 45 °.

Đường chéo của hình vuông trở thành cạnh huyền của tam giác vuông và hai cạnh còn lại của hình vuông trở thành hai cạnh (đáy và đối diện) của tam giác vuông.

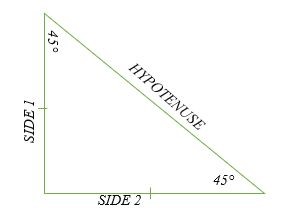
Tam giác vuông 45 ° -45 ° -90 ° đôi khi còn được gọi là tam giác vuông cân vì nó có độ dài hai cạnh bằng nhau và hai góc bằng nhau.

Chúng ta có thể tính cạnh huyền của tam giác vuông 45 ° -45 ° -90 ° như sau:

Cho cạnh 1 và cạnh 2 của tam giác vuông cân là x.

Áp dụng Định lý Pitago a 2 + b 2 = c 2 , trong đó a và b là cạnh 1 và 2 và c là cạnh huyền.

x 2 + x 2 = 2x 2

Tìm căn bậc hai của mỗi số hạng trong phương trình

√x 2 + √x 2 = √ (2x 2 )

x + x = x √2

Do đó, cạnh huyền của một góc 45 °; 45 °; 90 ° tam giác là x √2

Làm thế nào để giải quyết một tam giác 45 ° -45 ° -90 °?

Với độ dài của một cạnh của hình tam giác là 45 ° -45 ° -90 °, bạn có thể dễ dàng tính toán còn lại thiếu độ dài cạnh mà không cần dùng đến các phương pháp như Định lý Pitago hoặc các hàm lượng giác.

Các phép tính của một tam giác vuông 45 ° -45 ° -90 ° rơi vào hai khả năng:

• Trường hợp 1

Để tính độ dài cạnh huyền khi cho độ dài của một cạnh, nhân độ dài đã cho với √2.

• Trường hợp 2

Khi cho độ dài cạnh huyền của tam giác 45 ° -45 ° -90 °, bạn có thể tính độ dài cạnh bằng cách chia cạnh huyền cho √2.

Lưu ý: Chỉ có thể giải các tam giác 45 ° -45 ° -90 ° bằng phương pháp tỷ lệ 1: 1: √2.

ví dụ 1

Cạnh huyền của một góc 45 °; 45 °; 90 ° tam giác là 6√2 mm. Tính độ dài của cơ sở và chiều cao của nó.

Giải pháp

Tỷ lệ 45 °; 45 °; 90 ° tam giác là n: n: n√2. Vì vậy chúng tôi có;

⇒ n√2 = 6√2 mm

Bình phương cả hai vế của phương trình.

⇒ (n√2) 2 = (6√2) 2 mm

⇒ 2n 2 = 36 * 2

⇒ 2n 2 = 72

n 2 = 36

Tìm căn bậc hai.

n = 6 mm

Do đó, mỗi đáy và chiều cao của tam giác vuông là 6 mm.

Ví dụ 2

Tính độ dài các cạnh của một tam giác vuông có một góc là 45 ° và cạnh huyền là 3√2 inch.

Giải pháp

Cho một góc của tam giác vuông là 45 độ, thì đây phải là tam giác vuông 45 ° -45 ° -90 °.

Do đó, chúng ta sử dụng tỷ lệ n: n: n√2.

Hypotenuse = 3√2 inch = n√2;

Chia cả hai vế của phương trình cho √2

n√2 / √2 = 3√2 / √2

n = 3

Do đó, chiều dài của mỗi cạnh của hình tam giác là 3 inch.

Ví dụ 3

Cạnh ngắn hơn của tam giác vuông cân là 5√2 / 2 cm. Đường chéo của tam giác là gì?

Giải pháp

Một tam giác vuông cân bằng với tam giác vuông 45 ° -45 ° -90 °. Vì vậy, chúng ta áp dụng tỷ lệ n: n: n√2 để tính độ dài cạnh huyền.

Cho biết n = 5√2 / 2 cm;

⇒ n√2 = (5√2 / 2) √2

⇒ (5/2) √ (2 x 2)

⇒ (5/2) √ (4)

⇒ (5/2) 2

= 5

Do đó, hai chân của tam giác mỗi cạnh là 5 cm.

Ví dụ 4

Đường chéo của một tam giác vuông 45 ° -45 ° -90 ° là 4 cm. Chiều dài của mỗi chân là bao nhiêu?

Giải pháp

Chia cạnh huyền cho √2.

⇒ 4 / √2

⇒ √4 / √2

⇒ 4√2 / 2

= 2√2 cm.

Ví dụ 5

Đường chéo của hình vuông là 16 inch, tính độ dài của các cạnh,

Giải pháp

Chia đường chéo hoặc cạnh huyền cho √2.

⇒ 16 / √2

⇒ 16√2 / √2 = 8√2

Do đó, chiều dài của mỗi chân là 8√2 inch.

Ví dụ 6

Góc nâng của đỉnh tòa nhà từ một điểm trên mặt đất cách chân tòa nhà 10 m là 45 độ. Chiều cao của tòa nhà là bao nhiêu?

Giải pháp

Cho một góc là 45 độ, giả sử một tam giác vuông 45 ° – 45 ° -90 °.

Áp dụng tỷ lệ n: n: n√2 trong đó n = 10 m.

⇒ n√2 = 10√2

Do đó, chiều cao của tòa nhà là 10√2 m.

Ví dụ 7

Tìm độ dài cạnh huyền của một hình vuông có độ dài cạnh là 12 cm.

Giải pháp

Để có độ dài cạnh huyền, nhân độ dài cạnh với √2.

⇒ 12 √2 = 10 √2

Do đó, đường chéo là 10 √2 cm.

Xem thêm:

3 4 5 Hình tam giác vuông là gì và cách giải chi tiết nhất

Tam giác 30-60-90 là gì? Hướng dẫn cách giải hay nhất

Ví dụ 8

Tìm độ dài của hai cạnh còn lại của hình vuông có đường chéo 4√2 inch.

Giải pháp

Một nửa hình vuông tạo thành tam giác vuông 45 ° – 45 ° -90 °, do đó, chúng ta sử dụng tỷ lệ n: n: n√2.

n√2 = 4√2 inch.

chia cả hai vế cho √2

n = 4

Do đó, độ dài các cạnh của hình vuông mỗi cạnh là 4 inch.

Ví dụ 9

Tính đường chéo của một vườn hoa hình vuông có độ dài các cạnh là 30 m.

Giải pháp

Áp dụng tỷ lệ n: n: n√2, trong đó n = 30.

⇒ n√2 = 30 √2

Do đó, đường chéo bằng 30 √2 m