Số hữu tỉ là gì? Sự khác nhau giữa số hữu tỉ và số vô tỉ

Định nghĩa và công thức của số hữu tỉ là một trong những kiến thức cực kỳ quan trọng mà các bạn học sinh cấp ba cần phải hiểu rõ. Để xây dựng nền tảng toán học vững chắc, hãy cùng Monkey điểm qua tất cả các yếu tố cần học về số hữu tỉ trong bài viết này nhé!

1. Số hữu tỉ là gì?

Trong toán học, cụ thể là đại số, số hữu tỉ là các số x có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên với b khác 0. Tập hợp các số hữu tỉ, hay còn gọi là trường số hữu tỉ, có ký hiệu là Q.

Số hữu tỉ bao gồm:

• Số thập phân hữu hạn: 0.5 (½), 0.2 (⅕),…

• Số thập phân vô hạn tuần hoàn: 0.16666… (⅙), 0.3333… (⅓),…

• Tập hợp số nguyên (Z): -2, -1, 0, 1, 2,…

• Tập hợp số tự nhiên (N): 1, 2, 3, 4, 5, 6,…

Tính chất của số hữu tỉ:

• Tập hợp số hữu tỉ là tập hợp đếm được.

• Phép nhân số hữu tỉ có dạng

• Phép chia số hữu tỉ có dạng:

• Nếu số hữu tỉ là số hữu tỉ dương thì số đối của nó là số hữu tỉ âm và ngược lại. Tức tống số hữu tỉ và số đối của nó bằng 0.

Xem thêm: Nguyên hàm từng phần là gì? Công thức tính nguyên hàm từng phần cơ bản và nâng cao đầy đủ nhất

1.1 Số hữu tỉ âm là gì? Số hữu tỉ dương là gì?

Theo định nghĩa toán học chuẩn xác nhất, thì số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm. Ngược lại, số hữu tỉ lớn hơn 0 sẽ được gọi là số hữu tỉ dương. Lưu ý rằng, số 0 không phải là số hữu tỉ âm và cũng không phải là số hữu tỉ dương.

1.2 Các phép toán cơ bản với số hữu tỉ

Phép tính cộng trừ

Sau đây là các bước mà bạn có thể áp dụng để tính các phép toán cộng trừ với các số hữu tỉ.

Bước 1: Viết các số hữu tỉ dưới dạng phân số

Bước 2: Áp dụng quy tắc cộng, trừ và các tính chất để tính

Quy tắc cộng, trừ: Đưa các số hữu tỉ về cùng mẫu (quy đồng, rút gọn,…) rồi cộng, trừ tử số, giữ nguyên mẫu số.

Tính chất:

• Tính chất giao hoán: x + y = y + x

• Tính chất kết hợp: (x + y) + z = x + (y + z)

• Tính chất cộng với 0: x + 0 = 0 + x = x

Bước 3: Rút gọn kết quả (nếu có thể)

Phép tính nhân chia

• Nhân hai số hữu tỉ:

• Chia hai số hữu tỉ:

1.3 Các phép tính và công thức toán khác với số hữu tỉ

Bên cạnh các phép tính cơ bản kể trên, thì các bạn còn cần phải lưu ý một số phép tính và công thức liên quan đến số hữu tỉ thường gặp sau.

Giá trị tuyệt đối của 1 số hữu tỉ

Giá trị tuyệt đối của một số hữu tỉ x được kí hiệu là |x|, là khoảng cách từ điểm x tới điểm O trên trục số.

• Nếu x > 0 thì |x| = x.

• Nếu x = 0 thì |x| = 0.

• Nếu x < 0 thì |x| = -x.

Dựa vào định nghĩa trên, công thức xác định giá trị tuyệt đối của 1 số hữu tỉ như sau:

Công thức tính lũy thừa của 1 số hữu tỉ

Các công thức tính lũy thừa của 1 số hữu tỉ mà bạn cần phải ghi nhớ:

1.4 Cách so sánh hai số hữu tỉ

Để so sánh hai số hữu tỉ x, y ta có thể làm như sau:

• Viết x, y dưới dạng phân số cùng mẫu dương.

x = a /m; y = b/m ( m > 0)

• So sánh các tử là số nguyên a và b

  • Nếu a > b thì x > y

  • Nếu a = b thì x = y

  • Nếu a < b thì x < y

Lưu ý:

• Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương, và được biểu diễn bởi các điểm bên phải gốc O trên trục số.

• Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm, và được biểu diễn bởi các điểm bên trái gốc O trên trục số.

• Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm

1.5 Một số dạng bài tập mẫu về số hữu tỉ có lời giải

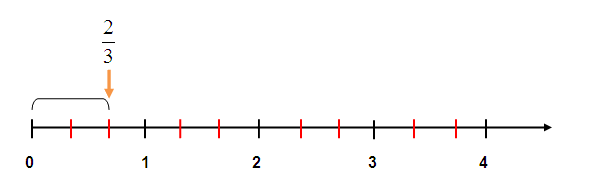
Bài tập 1: Số -3/14 là hiệu của hai số hữu tỉ nào dưới đây?

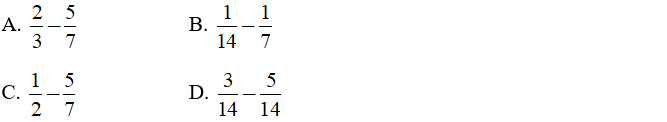
Đáp án:

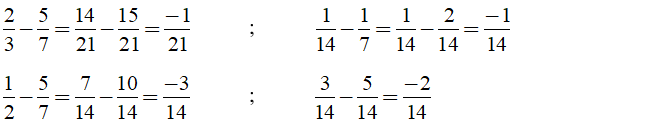
Kết luận: Chọn đáp án C

Bài tập 2: Tìm x,y,z biết rằng: (x−15)(y+12)(z−3)= 0 Và x+1 = y+2 = z+3.

Đáp án:

Ta có: (x−15)(y+12)(z−3)=0

⇔x−15=0 hoặc y+12=0 hoặc z−3=0

⇔x=15 hoặc y=−12 hoặc z=3

• • Nếu x=15, kết hợp với x+1=y+2=z+3 ta suy ra y=−45;z=−95

  • Nếu y=−12, kết hợp với x+1=y+2=z+3 ta suy ra x=12;z=−32

  • Nếu z=3, tương tự ta suy ra x=5;y=4

Vậy ta có ba bộ số thỏa mãn đó là:

15;−45;−95 hoặc 12;−12;−32 hoặc 5;4;3.

Bài tập 3: Tìm x∈Q biết: (23x−15)(35x+23)<0.

Đáp án:

Ta có: (23x−15)(35x+23)<0

⇔[23(x−310)][35(x+109)]<0

⇔23.35(x−310)(x+910)<0

⇔(x−310)(x+109)<0

Từ đó suy ra: x−310 và x+109 trái dấu, mặt khác ta lại có x−310<x+109

Nên suy ra: x−310<0 và x+109>0⇔−109<x<310.

Vậy các số hữu tỉ x thỏa mãn bài toán là −109<x<310.

2. Số vô tỉ là gì?

Trong toán học, các số vô tỉ là tất cả các số thực không phải là số hữu tỉ, mà là các số được xây dựng từ các tỷ số (hoặc phân số) của các số nguyên. Số vô tỉ là các số viết được dưới dạng số thập phân vô hạn không tuần hoàn. Và kí hiệu của số vô tỉ là I.

Các bạn cần ghi nhớ các số thực không phải là số hữu tỉ có nghĩa là các bạn không thể biểu diễn được dưới dạng tỉ số như a/ b (trong đó a, b là các số nguyên).

Tính chất của số vô tỉ: Tập hợp số vô tỉ là tập hợp không đếm được.

Ví dụ:

• Số vô tỉ: 0,1010010001000010000010000001… (đây là số thập phân vô hạn không tuần hoàn)

• Số căn bậc 2: √2 (căn 2)

• Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

3. Sự khác nhau giữa số hữu tỉ và số vô tỉ

• Số hữu tỉ bao gồm số thập phân vô hạn tuần hoàn, còn số vô tỉ là các số thập phân vô hạn không tuần hoàn.

• Số hữu tỉ chỉ là phân số, còn số vô tỉ có rất nhiều loại số khác nhau

• Số hữu tỉ là số đếm được, còn số vô tỉ là số không đếm được

Hy vọng, thông qua những chia sẻ trên của Monkey sẽ giúp bạn phần nào hiểu được hết khái niệm và các công thức tính toán về số vô tỉ. Đồng thời, qua đó hỗ trợ bạn xây dựng và tiếp thu kiến thức nâng cao một cách tốt hơn trên lớp. Xin được đồng hành cùng bạn.