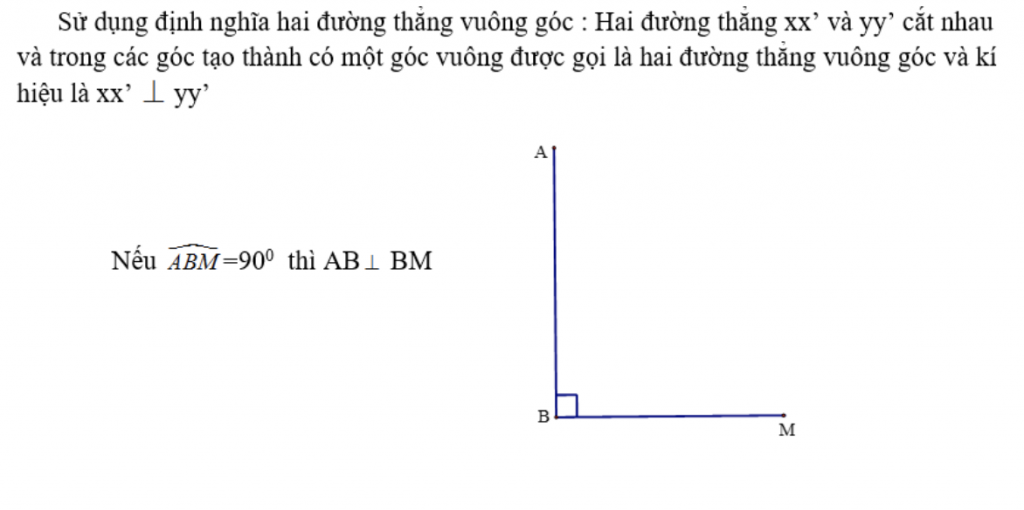
Để chứng minh hai đường thẳng vuông góc chúng ta chứng minh mai đường thẳng đó cắt nhau và tạo ra một góc 90.
Phương pháp số 2 – Tính chất từ vuông góc đến song song
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại (Hoặc phát biểu khác Có một đường thẳng thứ 3 vừa song song với đường thẳng thứ nhất vừa vuông góc với đường thẳng thứ hai.)
Phương pháp số 3 – Tính chất hai tia phân giác của góc kề bù
Tính chất: Góc tạo bởi hai tia phân giác của 2 góc kề bù bằng 90 (Hình học Lớp 6)

Phương pháp số 4 trong việc chứng minh hai đường thẳng vuông góc – tính chất trực tâm của tam giác
Tính chất: Đường thẳng đi qua trực tâm của tam giác và đỉnh thì vuông góc với cạnh đối diện

Phương pháp số 5 – Hai đường thẳng chứa hai cạnh của tam giác vuông
Hai đường thẳng chứa hai cạnh của tam giác vuông thì vuông góc với nhau
![]()
Phương pháp số 6 – Trung trực của đoạn thằng
Tính chất : Mọi điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
![]()
d là trung trực của AB tại I suy ra d vuông góc với AB
Phương pháp số 7 – Hai đường thẳng chứa hai đường chéo của hình vuông hoặc hình thoi
Theo tính chất của hình vuông và hình thoi: Hai đường chéo của hình vuông (hoặc hình thoi) vuông góc với nhau. Vậy nên nếu hai đường thẳng chứa hai đường chéo của hình vuông (hoặc hình thoi) thì chúng vuông góc.
Phương pháp số 8 – Sử dụng tính chất đường kính và dây cung trong đường tròn.
Đường kính của đường tròn vuông góc với dây cung vì vậy để chứng minh hai đường thằng vuông góc chúng ta chứng minh chúng đi qua đường kính và dây cung của đường tròn.
Phương pháp số 9 sử dụng định lý Pytago đảo
![]()
Phương pháp số 10 – Sử dụng tính chất của tam giác cân, tam giác đều
Để chứng minh hai đường thẳng vuông góc ta tìm cách chứng minh một đường là cạnh đáy của tam giác cân (hoặc tam giác đều) đường còn lại là trung tuyến hoặc là trung trực ứng với cạnh đó.
Phương pháp số 11 – Sử dụng tính chất tiếp tuyến trong đường tròn
Bài tập chứng minh hai đường thẳng vuông góc
Bài 1: Cho tam giác ABC đều. Trên cạnh AB lấy điểm B sao chư=2 48 . Từ D kẻ đường thăng vuông góc với AB cắt AC ở E. Qua E kẻ đường thăng vuông góc với AC cắt BC ở E. Chứng minh DF vuông góc với BC.
Bài 2: Cho tam giác ABC. Kẻ BD vuông góc với AC, CE vuông góc với AB. Trên tia đối của tỉa BD lấy điểm M sao cho BM = AC. Trên tia đối cuả tia CE lấy điểm N sao cho CN = AB. Chứng minh AM vuông góc với AN.
Bài 3: Cho tam giác ABC có góc A bằng 75. độ, góc B bằng 60 độ. Trên nửa mặt phăng bờ BC chứa điểm A vẽ tia Bx sao cho góc CBx bằng 15°. Từ A vẽ một đường thăng vuông góc với AB cắt Bx tại D. Chứng minh DC vuông góc với BC.
Bài 4: Cho tam giác ABC vuông ở A có CD là phân giác. Kẻ BH vuông góc với CD, gọi E là điểm trên tia đối của tia HC sao cho HE = HD. Chứng minh EB vuông góc với BC.
Bài 5: Cho tam giác ABC vuông ở A. Gọi H là chân đường vuông góc kẻ từ A xuống BC, gọi I là trung điểm của BC. Gọi K và L là các hình chiếu vuông góc của H trên AB và AC theo thứ tự đó. Chứng minh AI vuông góc với KL.
Bài 6: Cho tam giác ABC, vẽ tam giác ABD vuông cân tại D (Avà D khác phía đối với BC). Vẽ tam giác CBG vuông cân tại B (G và A cùng phía đối với BC). Chứng minh GA vuông góc với DC.
Bài 7: Cho tam giác ABC vuông ở A. Gọi H là chân đường vuông góc kẻ từ A xuống BC, gọi I là trung điểm của BC. Gọi K và L là các hình chiếu vuông góc của H trên AB và AC theo thứ tự đó. Chứng minh AI vuông góc với KL.
Bài 8: Cho tam giác ABC có BD là tia phân giác của góc B. D thuộc AC. Vẽ đường thăng xy qua A và song song với BD. Gọi M là giao điểm của xy với BC. Kẻ BN là tia phân giác của góc ABM, N thuộc AM. Chứng minh BN vuông góc với AM tại N.
Bài 9: Cho tam giác ABC, I là trung điểm của BC. Đường thăng vuông góc với AB tại B cắt đường thăng AI tại D. Trên tia đối của tia ID lấy điểm E sao cho IE bằng ID. Gọi H là giao điểm của CE và AB. Chứng minh CH vuông góc AB.
Bài 10: Cho tam giác ABC vuông cân tại A. Trên nửa mặt phăng bờ AC chứa điểm B vẽ tia Cx vuông góc với AC. Gọi M là một điểm bất kỳ thuộc AC. Trên tia Cx lấy điểm N sao cho CN = CM. Gọi I là trung điểm của BM, gọi K là trung điểm của AC. Chứng minh IK vuông góc với AN. ( HD: Kẻ BH vuông góc với AN, H thuộc AC)
Bài 11: Cho tam giác ABC góc B bằng 909, đường cao BH. Gọi M là trung điểm của BH, K là điểm đối xứng với C qua B. Chứng minh KH vuông góc với AM. (HD: Gọi N là trung điêm của HC)
Bài 12: Cho tam giác ABC cân tại A. Đường cao AH, kẻ HE vuông góc với AC. Gọi O là trung điểm của EH, I là trung điểm của EC. Chứng minh:
a) IO vuông góc với AH. b) AO vuông góc với BE.
Bài 13: Cho tam giac ABC vuông tại A, đường cao AH. Gọi E là trung điểm của BH, F là trung điểm của AH. Chứng minh CF vuông góc với AE.
Bài 14: Cho tam giác ABC vuông tại A, đường cao AH, phân giác AD. Gọi I K lần lượt là các điểm cách đều 3 cạnh của tam giác ABH và ACH. Gọi E là giao điểm của BI với AK. Chứng minh:
a) BE vuông góc với AK.
b) IK vuông góc với AD.




