Trục Đối Xứng Là Gì ? Nghĩa Của Từ Trục Đối Xứng Trong Tiếng Việt

Các em sẽ được tìm hiểu về đối xứng trục trong bài viết này. Phần 1 là phần lý thuyết, bao gồm định nghĩa về trục đối xứng là gì, các loại hình có trục đối xứng. Phần 2 là phần bài tập kèm hướng dẫn giải chi tiết để các em ôn tập và củng cố kiến thức. Đang xem: trục đối xứng là gì?

LÝ THUYẾT VÀ BÀI TẬP ĐỐI XỨNG TRỤC

A. LÝ THUYẾT

A. Lý thuyết

1. Hai điểm đối xứng nhau qua một đường thẳng

Định nghĩa: Hai điểm đối xứng nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.

Nếu điểm M∈d”>M∈d thì điểm đối xứng với M qua d cũng chính là điểm M.

2. Hai hình đối xứng với nhau qua một đường thẳng

Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại.

Hình đối xứng qua một đường thẳng d của:

– Một đường thẳng là một đường thẳng.

– Một đoạn thẳng là một đoạn thẳng.

– Một góc là một góc bằng nó.

– Một tam giác là một tam giác bằng nó.

– Một đường tròn là một đường tròn có bán kính bằng bán kính đường tròn đã cho.

3. Hình có trục đối xứng

Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.

Một số hình có trục đối xứng quen thuộc:

– Một đoạn thẳng có trục đối xứng là đường trung trực của đoạn thẳng ấy.

Xem thêm: Hằng số Pi (π): Lịch sử phát hiện và ứng dụng trong toán học của số pi kì bí

– Một góc có trục đối xứng là tia phân giác của góc.

– Hai đường thẳng giao nhau có trục đối xứng là hai đường thẳng chứa các phân giác của các góc do hai đường thẳng tạo nên; hai trục đối xứng này vuông góc với nhau.

– Tam giác cân có một trục đối xứng là đường cao cũng là phân giác, trung tuyến, thuộc cạnh đáy. Tam giác đều có ba trục đối xứng.

– Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm của hai đáy.

4.Trục đối xứng của một số hình

• Đối với đường tròn, trục đối xứng là đường kính của đường tròn. Một đường tròn có vô số trục đối xứng.
• Trong tam giác cân, trục đối xứng là đường cao, trực tâm, đường trung tuyến và đường phân giác của tam giác cân xuất phát từ đỉnh ứng với đáy. Một tam giác cân chỉ có một trục đối xứng.
• Trong một tam giác đều, trục đối xứng là đường cao, đường trung trực và đường trung trực của tam giác đều. Một tam giác đều có 3 trục đối xứng.
• Đối với hình thang cân, trục đối xứng là đường thẳng đi qua trung điểm của hai đáy của hình thang cân. Hình thang cân có một trục đối xứng.
• Đối với hình thoi, các trục đối xứng là hai đường chéo của hình thoi. Một hình thoi có 2 trục đối xứng.
• Trong một hình vuông, các trục đối xứng là hai đường chéo của hình vuông và hai đường thẳng đi qua trung điểm của mỗi cặp cạnh đối diện của hình vuông. Một hình vuông có bốn trục đối xứng.
• Trong một hình chữ nhật, trục đối xứng là hai đường thẳng đi qua trung điểm của mỗi cặp cạnh đối diện của hình chữ nhật. Một hình chữ nhật có 2 trục đối xứng.
• Một đa giác đều có n cạnh thì có n trục đối xứng

Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

B. BÀI TẬP

Bài 1. Vẽ hình đối xứng với các hình đã cho qua trục d (h.58).

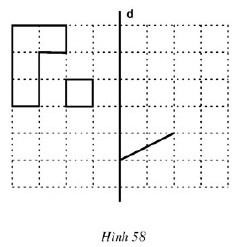
Lời giải:

Vẽ hình:

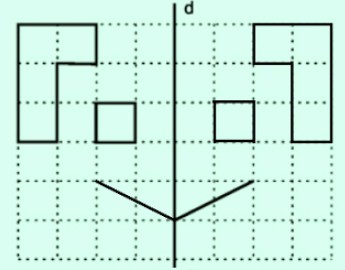
Bài 2. Cho góc xOy có số đo 50o, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

Xem thêm: Chuyển Đổi Diện Tích, Acre Là Gì, Nghĩa Của Từ Acre

a) So sánh các độ dài OB và OC

b) Tính số đo góc BOC

Lời giải:

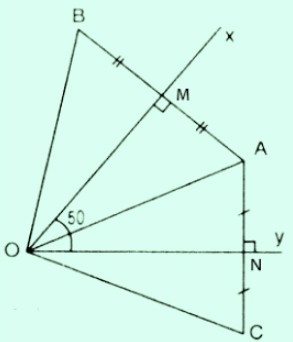
a) Ox là đường trung trực của AB => OA = OB

Oy là đường trung trực của AC => OA = OC

=> OB = OC

b) ΔAOB cân tại O (vì OA = OB)

Tam giác AOB cân tại O có OM là đường cao nên cũng là đường phân giác của góc AOB.

trục đối xứng là gì trục đối xứng thế nào là trục đối xứng tâm đối xứng và trục đối xứng là gì trục đối xứng là j truc doi xung la gi truc doi xung thế nào là hình có trục đối xứng khái niệm trục đối xứng định nghĩa trục đối xứng

Nguồn: cungdaythang.com