Số nguyên là gì? Khái niệm & các tập hợp số cơ bản khác

Số nguyên là một khái niệm phổ biến trong lĩnh vực số học. Bạn đã hiểu đúng ý nghĩa của nó chưa? Hãy cùng Kiến thức máy móc khám phá thêm về khái niệm này nhé!

Số nguyên là một khái niệm cơ bản quan trọng trong toán học. Nó bao gồm các số nguyên dương và số nguyên âm. Số 0 cũng được coi là một số nguyên và là điểm giới hạn giữa số âm và số dương.

Miền nguyên trong toán học được định nghĩa là tập hợp các số nguyên được sắp xếp theo một thứ tự duy nhất. Các số dương trong miền nguyên được sắp xếp theo một thứ tự logic, tuân theo quy luật của phép cộng. Một cách đơn giản và dễ hiểu hơn, số nguyên là các số có thể biểu thị mà không cần sử dụng thành phần phân số.

Tập hợp số nguyên Z

Khái niệm

Tập hợp số nguyên Z được ký hiệu từ chữ Zahl trong tiếng Đức, có nghĩa là chữ số. Nó là một tập hợp con của tập hợp số hữu tỉ Q và số thực R. Ngoài ra, Z cũng là tập hợp mẹ của tập hợp số tự nhiên N. Tương tự như tập hợp số tự nhiên, tập hợp số nguyên Z là vô hạn nhưng có thể đếm được. Nó có thể được chia thành hai tập hợp con là Z+ và Z-.

Z+ là tập hợp các số nguyên dương đại diện cho các số lớn hơn 0.

Tập hợp Z bao gồm các số nguyên âm nhỏ hơn 0.

Số 0 chỉ thuộc tập hợp Z và không thuộc tập hợp con Z+ và Z-.

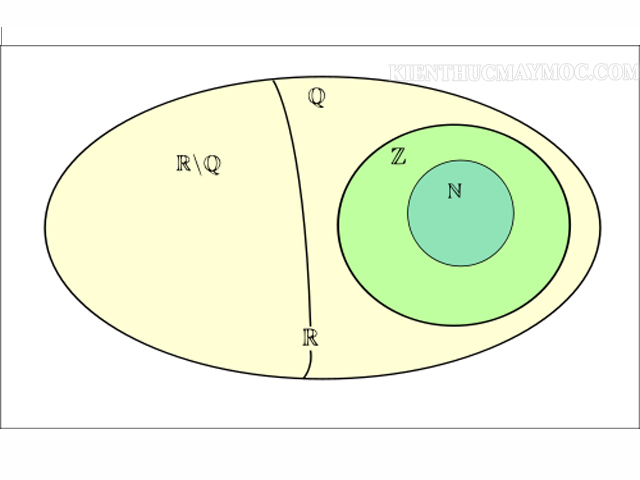
Tính chất của tập Z

Tính chất cơ bản của các số nguyên thuộc tập Z như sau:

Không có khái niệm số nguyên tối đa và số nguyên tối thiểu. Khái niệm tối đa và tối thiểu chỉ có tính tương đối và phụ thuộc vào điều kiện trong từng trường hợp.

Số nhỏ nhất mà là số nguyên dương là 1. Số lớn nhất mà là số nguyên âm là -1.

Z là một số nguyên bao gồm vô số tập con hữu hạn. Mỗi tập con sẽ được xác định bởi số nguyên nhỏ nhất và lớn nhất.

Không có số nguyên nào nằm giữa hai số nguyên liên tiếp.

Các tập hợp số cơ bản khác

Tập hợp số tự nhiên N

N là ký hiệu của tập hợp các số tự nhiên, đây là tập hợp nhỏ nhất trong hệ thống các tập hợp số. Tập hợp này bao gồm các số 0, 1, 2, 3, …. Các số này được sử dụng để đếm, ghi chép và lưu trữ thông tin. Đây là tập hợp số đầu tiên được hình thành trong lịch sử loài người.

Con số đã tồn tại từ lâu đời trên khắp thế giới, xuất hiện trong các nền văn hóa cổ đại như Babylon và Ai Cập. Tuy nhiên, khái niệm tập hợp số tự nhiên chỉ mới xuất hiện trong thời đại hiện đại vào thế kỷ 19. Tập hợp N, trong lĩnh vực lý thuyết tập hợp và khoa học máy tính, được coi là nền tảng đầu tiên.

Ví dụ:….

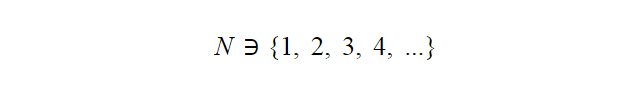
Tập hợp số hữu tỉ Q

Q là tập hợp các số hữu tỉ, tức là các số có thể được biểu diễn dưới dạng phân số a/b, với điều kiện cả a và b đều là số nguyên và b khác 0. Q tương tự như tập N hay Z, đều là tập hợp vô hạn nhưng có thể đếm được. Một số hữu tỉ có thể có nhiều biểu diễn khác nhau dưới dạng phân số và cũng có thể được biểu diễn dưới dạng số thập phân. Khi biểu diễn dưới dạng số thập phân, số hữu tỉ có thể là số thập phân tuần hoàn hoặc số thập phân không tuần hoàn.

Ví dụ:….

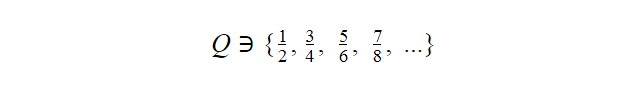
Tập hợp số vô tỉ I

I là một tập hợp gồm các số vô tỉ – những số không thể được biểu diễn dưới dạng phân số. Số vô tỉ thường được hiểu là các số thực không phải là số hữu tỉ. Một nhà toán học theo trường phái Pythagore đã đặt ra vấn đề về sự tồn tại của số vô tỉ khi ông cố gắng xác định độ dài các cạnh của một ngôi sao năm cánh bằng phương pháp Pythagore. Ông nhận ra rằng cần có một đơn vị nhỏ phù hợp để đo độ dài các cạnh của ngôi sao và số đó không thể được biểu diễn dưới dạng tỉ số của hai số nguyên.

Ví dụ:….

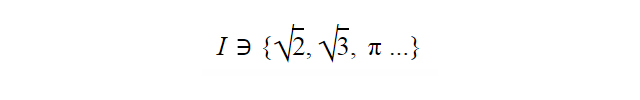
Các nhà toán học Hy Lạp đã đặt tên cho chúng là các số không thể đo lường hoặc biểu diễn. Sau đó, nhà toán học Hy Lạp Theodorus của Cyrene đã thành công trong việc chứng minh tính vô tỉ bằng cách rút gọn căn bậc hai của các số nguyên nhỏ hơn 17. Từ đó, nhà toán học Hy Lạp Eudoxus của Cnidus đã xây dựng một nền tảng vững chắc để nghiên cứu các số vô tỉ.

Tập hợp số thực R

R là tập hợp các số thực, bao gồm các số tự nhiên, số nguyên, số hữu tỉ và vô tỉ. Nó là tập hợp số lớn nhất và được coi là một hệ thống đại số to lớn. Trừ số 0 ở trung tâm trục số, các số thực khác có thể là số âm hoặc số dương. R và các tập con khác đều là tập hợp vô hạn. Tuy nhiên, quy mô của R rất lớn đến mức không thể đếm được số lượng số thực.

Khái niệm số thực được sử dụng lần đầu trong thế kỷ 17 bởi nhà toán học người Pháp René Descartes nhằm biểu diễn giá trị nghiệm của đa thức và phân biệt chúng với các nghiệm ảo. Tuy nhiên, đến năm 1871, nhà toán học Georg Cantor đã công bố khái niệm chính xác nhất và vẫn được sử dụng cho đến ngày nay về số thực.

Ví dụ:….

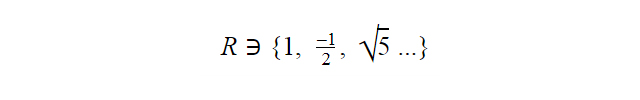
Tập hợp số phức C

Tập hợp C chứa các số phức có dạng a + bi, trong đó a và b là số thực và i là đơn vị ảo. Tính chất biểu diễn này cho phép số phức được phân thành hai phần: phần thực và phần ảo.

Khái niệm số học này được tạo ra bởi nhà toán học người Ý Gerolamo Cardano vào thế kỉ XIV. Ban đầu, nó được áp dụng để giải các phương trình bậc ba. Tuy nhiên, sau đó số phức đã được sử dụng để giải quyết những bài toán mà không thể tìm được nghiệm là số thực. Khái niệm này đã được áp dụng trong nhiều lĩnh vực khoa học khác nhau như khoa học kỹ thuật, điện từ học, cơ học, vật lý lượng tử và lý thuyết hỗn loạn trong toán học ứng dụng.

Trên đây là bài viết giới thiệu về khái niệm số nguyên và các tập hợp số cơ bản trong đại số. Mong rằng bài viết này đã cung cấp đầy đủ thông tin về các con số cho bạn. Đừng quên ghé thăm website của chúng tôi để cập nhật thêm kiến thức vật lý thú vị hàng ngày nhé!