Bài viết bao gồm ba phần: lý thuyết, ví dụ và bài tâp. Phần lý thuyết nhắc lại các kiến thức mà các em đã học về hình thang cân và trục đối xứng, ngoài ra bổ sung thêm một số kiến thức nâng cao. Phần ví dụ đưa ra các ví dụ kèm theo hướng dẫn giải để các em làm quen và biết cách giải quyết bài toán theo hướng nào. Phàn bài tập gồm các bài toán tự giải để các em ôn lại phần kiến thức có trong bài viết.
Hình thang cân. Đối xứng qua trục.
A. NHỮNG GÌ CẦN GHI NHỚ.
1. Định nghĩa hình thang cân là gì.
Hình thang đều là hình thang có hai góc kề một đáy bằng nhau (h.14).
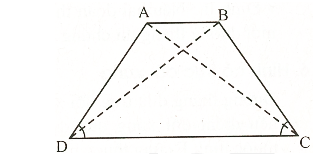
2. Đặc điểm của hình thang cân.
Trong hình thang có hai cạnh đáy bằng nhau:
Hai cạnh hai bên đều bằng nhau ;.
Hai đường chéo có độ dài tương đương nhau.
3. Các chỉ báo để nhận biết hình thang cân.
Hình thang có hai góc tiếp xúc một đáy bằng nhau là hình thang đều.
Hình thang có hai đường chéo đồng dài là hình thang cân.
4. Hai điểm đối xứng qua một đường thẳng.
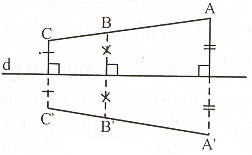
Hai điểm A và A’ được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng AA’ (h.15).
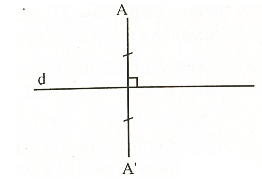
Quy ước: Nếu B thuộc đường thẳng d, thì điểm đối xứng với B qua d chính là chính B.
5. Hai hình đối xứng qua một đường trực.
Đường thẳng d là đường thẳng đối xứng của hai đoạn thẳng AB và A’B’.- Điều kiện để A đối xứng với A’ và B đối xứng với B’ qua d là khi hai đoạn thẳng AB và A’B’ là đối xứng với nhau qua đường thẳng d (h.16a).
Tam giác ABC và A’B’C’ được coi là đối xứng qua đường thẳng d nếu các điểm A, A’, B, B’, C và C’ đối xứng với nhau qua đường thẳng d (h.16b).
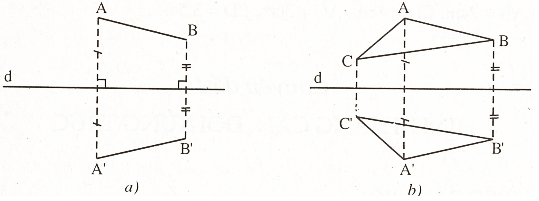
Hình 16.
• Định lý: Nếu có hai đoạn thẳng (hoặc hai góc, hai tam giác) đối xứng qua một đường thẳng, thì chúng có độ dài (hoặc độ lớn) bằng nhau.
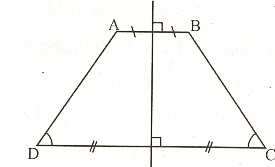
6. Hình có đối xứng qua trục.
Đường thẳng d được gọi là trục đối xứng của hình F nếu mọi điểm thuộc hình F khi đối xứng qua d cũng thuộc hình F.
Đường thẳng đi qua trung điểm của hai đáy của một hình thang cân được coi là trục đối xứng của hình thang cân (h.17) trong trường hợp đặc biệt.
7. Thêm vào.
Đầu tiên, ta giả sử có hai đường thẳng a và a’ đối xứng với nhau qua đường thẳng d. Điều này có nghĩa là nếu ta chọn hai điểm bất kỳ trên đường thẳng a, và chọn hai điểm tương ứng trên đường thẳng a’ sao cho cả bốn điểm này đều nằm trên đường thẳng d, thì chúng sẽ là đối xứng qua đường thẳng d.
Một hình có thể không có, có một, có nhiều hoặc vô số trục đối xứng.
Nếu ba điểm A, B, C nằm trên một đường thẳng (với B ở giữa A và C) và A’, B’, C’ là ba điểm đối xứng của chúng qua đường thẳng d, thì ba điểm A’, B’, C’ cũng nằm trên một đường thẳng (với B’ ở giữa A’ và C’).
B. Một số ví dụ.
Ví dụ 8. Trong tam giác ABC, với A là một góc vuông, điểm H di chuyển trên đoạn thẳng BC. Gọi E là điểm đối xứng của H qua đoạn thẳng AB và F là điểm đối xứng của H qua đoạn thẳng AC.
A) Chứng minh E, A, F nằm trên cùng một đường thẳng.
B) Chứng minh BEFC là một hình thang.
C) Tìm vị trí của H trên BC để BEFC là hình thang vuông.
Giải (h.19).
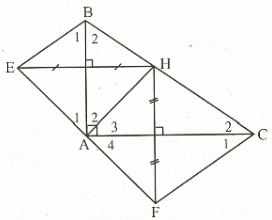
A) Theo tính chất đối xứng trụ, chúng ta có :.
\(\Widehat {{\rm{A}}_{\rm{1}}^{}}{\rm{ = }}\widehat {{\rm{A}}_{\rm{2}}^{}}{\rm{; }}\widehat {{\rm{A}}_{\rm{3}}^{}}{\rm{ = }}\widehat {{\rm{A}}_{\rm{4}}^{}}{\rm{.}}\) Không thay đổi.
EAF = A1 + A2 + A3 + A4 = 2(A2 + A3) = 180° => E, A, F cùng nằm trên một đường thẳng.
B) Dựa vào tính chất đối xứng trục, chúng ta có:.
\(\Widehat {{\rm{B}}_{\rm{1}}^{}}{\rm{ = }}\widehat {{\rm{B}}_{\rm{2}}^{}}{\rm{; }}\widehat {{\rm{C}}_{\rm{1}}^{}}{\rm{ = }}\widehat {{\rm{C}}_{\rm{2}}^{}}\).
Nên \(\widehat {{\rm{EBC}}}{\rm{ + }}\widehat {{\rm{FCB}}}{\rm{ = }}\widehat {{\rm{B}}_{\rm{1}}^{}}{\rm{ + }}\widehat {{\rm{B}}_{\rm{2}}^{}}{\rm{ + }}\widehat {{\rm{C}}_{\rm{1}}^{}}{\rm{ + }}\widehat {{\rm{C}}_{\rm{2}}^{}}{\rm{ = 2}}{\rm{.(}}\Widehat {{\rm{B}}_{\rm{2}}^{}}{\rm{ + }}\widehat {{\rm{C}}_{\rm{2}}^{}}{\rm{) = 180}}{{\rm{^{\circ}}}}{\rm{.}}\)Mà hai góc ở v
Trí trong cùng bên nên BE // CF hay BCFE là hình thang.
C) Theo tính chất đối xứng: Góc BEA bằng góc BHA.
Hình thang vuông BEFC có điều kiện tương đương với góc BEA bằng 90 độ và góc BHA bằng 90 độ, tức là AH là đường cao.
Cho tam giác ABC với AD là đường phân giác. Trong tam giác này, có một điểm M. Chúng ta đặt các điểm N, X, Y lần lượt là điểm đối xứng của M qua các đường thẳng AD, AB, AC. Chúng ta cần chứng minh rằng AN là đường trung trực của đoạn thẳng XY.
Giải.
Trường hợp 1. Giả sử \(\widehat {{\rm{MAB}}}{\rm{ }} \le {\rm{ }}\widehat {{\rm{MAC}}}\) (h.20).
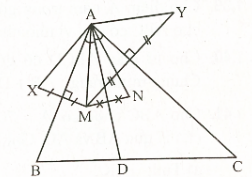
\(\Begin{array}{*{20}{l}}{\widehat {{\rm{XAB}}}{\rm{ = }}\widehat {{\rm{NAC}}}{\rm{ = }}\alpha {\rm{ ; }}\widehat {{\rm{NAD}}}{\rm{ = }}\beta }\\{\widehat {{\rm{YAC}}}{\rm{ = }}\alpha {\rm{ + 2}}{\rm{.}}\Beta {\rm{, suy ra}}}\\{\widehat {{\rm{NAY}}}{\rm{ = 2}}{\rm{.}}\Alpha {\rm{ + 2}}{\rm{.}}\Beta {\rm{ = }}\widehat {{\rm{NAX}}}{\rm{\;\;\;\;\;}}\left( {\rm{1}} \right)}\end{array}\)\(\begin{array}{*
Mặt khác: AX = AY = AN (2) cũng vậy.
Từ (1) và (2) có thể suy ra AN là đường trực của đoạn XY.
Trường hợp 2. Giả sử \(\widehat {{\rm{MAB}}}{\rm{ > }}\widehat {{\rm{MAC}}}\). Cũng giống như trường hợp 1.
Nhận xét: Dựa vào bài viết trên, có thể chứng tỏ được bài dưới đây :.
Tam giác ABC có điểm M bên trong. Điểm Y là điểm đối xứng của M qua cạnh AC, điểm X là điểm đối xứng của M qua cạnh AB. Điểm N nằm bên trong tam giác sao cho AN là đường trung trực của đoạn thẳng X, Y. Chứng minh rằng góc MAB bằng góc NAC.
C. BÀI TẬP.
1. Trong các đỉnh của hai tam giác đối xứng trục, luôn có bốn đỉnh tạo thành một hình thang cân. Tuy nhiên, bạn Nam lại không đồng ý với quan điểm này.
Ai đúng, ai sai, tại sao?
2. Cho tam giác ABC nhọn. Vẽ về phía bên ngoài tam giác ABC các đường thẳng Ax và Ay sao cho.
Cho tam giác ABC với \(\widehat {{\rm{xAB}}}{\rm{ = }}\widehat {{\rm{yAC}}}{\rm{ = }}\frac{1}{2}\widehat {{\rm{BAC}}}\). Trên tia Ax và Ay, lấy hai điểm M và N sao cho AM = AN và \(\widehat {{\rm{ABM}}}{\rm{ < }}\widehat {{\rm{ABC}}}\). Xét tam giác PBC, với \(\widehat {{\rm{PBC}}}{\rm{ = }}\widehat {{\rm{ABM}}}{\rm{;}}\) \(\widehat {{\rm{PCB}}}{\rm{ = }}\widehat {{\rm{ACN}}}\). Ta cần chứng minh rằng điểm P luôn nằm trên một đường thẳng cố định.
3. Trong tam giác ABC, với A là góc vuông, chúng ta lấy một điểm M bất kỳ trên cạnh BC. Tiếp theo, chúng ta gọi điểm E là điểm đối xứng của M qua cạnh AB và điểm F là điểm đối xứng của M qua cạnh AC.
A) Chứng minh rằng A là điểm chính giữa của EF.
B) Xác định vị trí của M để EF có chiều dài nhỏ nhất.
Cho tam giác cân ABC (AB = AC). Trên cạnh AB và AC, ta lấy hai điểm M và N sao cho tổng độ dài AM và AN bằng độ dài AB. Chúng ta cần chứng minh rằng trung điểm của cạnh AB, cạnh AC và đoạn thẳng MN thẳng hàng.
5. Cho tam giác ABC, trên tia phân giác ngoài của góc tại đỉnh C, ta chọn một điểm M nằm ngoài tia đó (M khác C). Chứng minh rằng tổng độ dài AC và CB nhỏ hơn tổng độ dài AM và MB.
Cho điểm A nằm trong góc xOy. Ta dựng ABC sao cho điểm B thuộc đường Ox và điểm C thuộc đường Oy, sao cho chu vi của tam giác ABC là nhỏ nhất.
Cho tứ giác ABCD có góc ngoài của tứ giác tại đỉnh C bằng góc ACB. Ta cần chứng minh rằng AB + DB > AC + DC.
Trong tam giác ABC có góc A bằng 70 độ. AH là đường cao. Ta gọi M, N lần lượt là điểm đối xứng của H qua AB và AC. Các điểm I, K là giao điểm của đường MN với AB và AC.
A) Tính góc IHK.
B) Chứng minh CI\( \bot \)AB ; BK\( \bot \)AC.
9. Trong tam giác ABC, chúng ta cần chứng minh rằng đường cao hₐ không lớn hơn √(p.(P – a)), trong đó BC = a và p là nửa chu vi của tam giác.
10. Chứng minh rằng các điểm E, F thuộc đường phân giác AD sao cho \(\widehat{{ABE}} = \widehat{{DBF}}\) và vẽ điểm I, H, K theo quy tắc đối xứng qua các cạnh AB, AC, BC.
A) FH = FI, FI = KE.
Góc ACE bằng góc DCF.
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết ở dưới đây.
Học trực tuyến lớp 8 trên Tuyensinh247.Com đảm bảo hỗ trợ học sinh lớp 8 đạt kết quả tốt, hoàn trả học phí nếu không đạt hiệu quả học tập.
Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!