Hằng đẳng thức là gì? 7 hằng đẳng thức đáng nhớ (có ví dụ)

Xin chào các bạn, trong buổi hôm nay chúng ta sẽ cùng khám phá về những hằng đẳng thức đáng nhớ và áp dụng cơ bản của chúng.

Đầu tiên, mình sẽ giới thiệu về định nghĩa. Tiếp theo, mình sẽ đưa ra một số ví dụ tiêu biểu và liệt kê các hằng đẳng thức cơ bản, mở rộng và tổng quát. Cuối cùng, mình sẽ cung cấp một ví dụ minh họa. Có vẻ như đã hoàn thành, phải không nhỉ? 😊

Phần quan trọng nhất trong bốn phần đã được giới thiệu là phần liệt kê các hằng đẳng thức và ví dụ minh họa. Hãy dành nhiều thời gian cho phần này nhé.

I. Hằng đẳng thức là gì?

Trước khi khám phá khái niệm về hằng đẳng thức, chúng ta phải xác định ý nghĩa của đẳng thức trước. Điều này sẽ giúp các bạn hiểu sâu hơn về bản chất của nó!

Đẳng thức là một cặp biểu thức được kết nối bởi dấu =.

Hằng đẳng thức là một đẳng thức mà luôn đúng với mọi giá trị được gán cho các biến trong nó.

Theo Wikipedia, hằng đẳng thức được định nghĩa là một chuỗi các đẳng thức có liên quan và được tổng hợp thành một hằng đẳng thức.

Ví dụ: Đẳng thức $(a+b)^2=a^2+2ab+b^2$ là một hằng đẳng thức bởi vì ….

$(A+b)^2 = a^2+2ab+b^2$

Cho mọi giá trị của a và b, đẳng thức luôn đúng.

Hằng đẳng thức $\frac{a+b}{2} \geq \sqrt{ab}$ không tồn tại vì hai biểu thức không được kết nối bởi dấu =.

II. Hằng đẳng thức dùng để làm gì?

Công cụ rewrite tiếng Việt có thể được sử dụng để tạo ra đoạn văn mới và sáng tạo hơn. Đoạn văn nhập vào có chứa thông tin về việc ứng dụng của hằng đẳng thức trong Toán học, đặc biệt là ….

Đoạn văn đã được viết lại: Thực hiện phân tích đa thức thành các nhân tử.

Tính toán giá trị của biểu thức.

Hệ phương trình đối xứng được giải.

III. Các hằng đẳng thức đáng nhớ

Có rất nhiều hằng đẳng thức khác nhau. Trong đây, tôi chỉ sẽ liệt kê các hằng đẳng thức thường gặp trong chương trình sách giáo khoa và tạm chia chúng thành ba nhóm.

#1. Các hằng đẳng thức cơ bản

Đoạn văn nhập vào đã được viết lại như sau: “Những hằng đẳng thức này là những kiến thức cơ bản và thường gặp khi giải toán, vậy nên bạn cần nhớ chúng như việc nhớ bảng cửu chương.”

Kết quả: Tích của một tổng $(a+b)^2$ bằng $a^2+2ab+b^2$.

$(A-b)^2=a^2-2ab+b^2$ được gọi là công thức bình phương của một hiệu.

Công thức $a^2-b^2=(a+b)(a-b)$ là kết quả của việc hiệu hai bình phương.

Ta có công thức lập phương của một tổng $(a+b)^3=a^3+3a^2b+3ab^2+b^3$.

$(A-b)^3$ là một hiệu bình phương được tính theo công thức $a^3-3a^2b+3ab^2-b^3$.

Công thức tổng hai lập phương $a^3+b^3=(a+b)(a^2-ab+b^2)$ được dùng để tính tổng của hai lập phương $a^3$ và $b^3$.

Công thức $a^3-b^3=(a-b)(a^2+ab+b^2)$ là hiệu hai lập phương.

Chú ý:.

Bạn có thể kết hợp hằng đẳng thức thứ nhất – thứ hai, thứ tư – thứ năm, thứ sáu – thứ bảy với nhau.

Có thể sử dụng tam giác Pascal để tạo ra các phương trình số 1, 2, 4, 5.

Ở đây, tôi chỉ sử dụng cách viết phổ biến nhất. Trong thực tế, bạn cần linh hoạt sử dụng công thức $(a+b)^2=a^2+2ab+b^2$ hoặc $a^2+2ab+b^2=(a+b)^2$ hoặc $a^2+b^2=(a+b)^2-2ab$ trong quá trình thực hành.

#2. Các hằng đẳng thức mở rộng

Dưới đây là những công thức mở rộng phổ biến, nếu bạn có thể ghi nhớ chúng, thì thật tuyệt vời.

$(A+b)^4=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4}$.

$(A+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$.

$(A+b+c)^{3}=a^{3}+b^{3}+c^{3}+3(a+b)(b+c)(c+a)$.

$A^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)$.

#3. Các hằng đẳng thức tổng quát

Những điều cụ thể thường khó hiểu và khó nhớ, trong khi những điều tổng quát thì dễ nhớ và dễ hiểu. Nếu bạn có thể hiểu và nhớ được những điều tổng quát, bạn không cần nhớ những trường hợp cụ thể.

Cho $a^n – b^n = (a – b)(a^{n-1} + a^{n-2}b + \cdots + ab^{n-2} + b^{n-1})$, với n là một số tự nhiên bất kỳ.

Cho $n$ là một số nguyên dương. Khi đó, công thức $(a+b)^n=\sum^n_{k=0}C^k_na^{n-k}b^k$ có thể được biểu diễn dưới dạng tổng các số hạng, trong đó $C^k_n$ được tính bằng công thức $\frac{n!}{K!(N-k)!}$ Với $k$ từ 0 đến $n$.

Chú ý.

Không tồn tại hằng đẳng thức $a^n+b^n$ với n là một số tự nhiên bất kỳ.

Khi muốn khai triển biểu thức $(a-b)^n$, hãy xem nó như là $[a+(-b)]^n$ và tiến hành khai triển.

IV. Bài tập ví dụ về hằng đẳng thức

Ví dụ 1. Phân tích đa thức $9x^2-6x+1$. thành nhân tử.

Cách 1:.

Lời giải:.

$9x^2-6x+1=(3x)^2-2(3x).1+1^2=(3x-1)^2$.

Cách 2:.

$f(x)=ax^2+bx+c=a(x-x_1)(x-x_2)$ với $x_1, x_2$ là nghiệm của đa thức $ax^2+bx+c$

Nghiệm của đa thức $ax^2+bx+c$ cũng chính là nghiệm của phương trình bậc hai $ax^2+bx+c=0$. Vậy thay vì phải mò mẫm nhẩm nghiệm của đa thức các bạn nên giải phương trình bậc hai tương ứng sẽ tiết kiệm được nhiều thời gian và công sức

Lời giải:.

Đa thức $9x^2-6x+1$. có một nghiệm kép là $\frac{1}{3}$.

=> $9x^2-6x+1=9\left(x-\frac{1}{3}\right)\left(x-\frac{1}{3}\right)=9\left(x-\frac{1}{3}\right)^2=(3x-1)^2$.

Cách 3:.

$9x^2-6x+1$.

$=9\left(x^2-\frac{6}{9}x+\frac{1}{9}\right)$.

$=9\left[\left(\frac{x^2}{x}-\frac{\frac{6}{9}x}{2x}\right)^2-\frac{1}{9}+\frac{1}{9}\right]$.

$=9\left[\left(x-\frac{1}{3}\right)^2\right]=9\left(x-\frac{1}{3}\right)^2=(3x-1)^2$.

Ví dụ 2. Tính giá trị biểu thức $A=a^2+b^2$ khi biết rằng a và b là nghiệm của phương trình $x^2+2x+3=0$.

Cách 1:.

Lời giải:.

$A=a^2+b^2=(a+b)^2-2ab$.

Khi áp dụng định lí Viète vào phương trình $x^2+2x+3=0$, ta thu được hệ thức $\left\{\begin{array}{ll}a+b&=-2\\ab&=3\end{array}\right.$.

Kết quả: Suy ra $A$ là bình phương của $a$ cộng với bình phương của $b$, tức là $A=a^2+b^2$. Đồng thời, $A$ cũng có thể được biểu diễn dưới dạng $(a+b)^2-2ab$. Áp dụng công thức này, ta có $A=(-2)^2-2.3=-2$.

Sử dụng máy tính Casio FX, chúng ta có thể áp dụng phương pháp số 2.

Cách giải:.

Bước 1: Lựa chọn phương pháp tính toán Equation/Func, sau đó chọn Polynomial và nhấn số 2 để tính phương trình bậc 2.

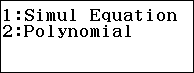
Tiến hành bước thứ hai bằng cách nhập các hệ số của phương trình….

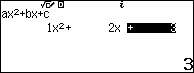
Sau bước 3, nhấn tổ hợp phím =, STO, và $(-)$.

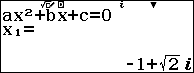
Bước 4. Nhấn phím bằng => nhấn phím lưu => nhấn phím độ.

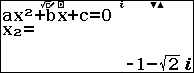
Bước 5. Lựa chọn phương pháp Complex.

Bước 6: Nhập biểu thức $A^2+B^2$ và nhấn phím ‘=’.

Ví dụ 3. Giải hệ phương trình sau:$\left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right$.

Cách 1:.

Lời giải:.

$\Left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x+y&=2 \\ (x+y)^2-2xy&=4\end{array}\right.$ Được viết lại thành $\left\{\begin{array}{ll}x+y&=2 \\ x^2+2xy+y^2-2xy&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right.$.

Đặt $S$ là tổng của $x$ và $y$, $P$ là tích của $x$ và $y$. Ta có hệ phương trình sau: $\left\{\begin{array}{ll}S&=2 \\ S^2-2P&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}S&=2 \\ 2^2-2P&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}S&=2 \\ P&=0\end{array}\right.$.

Theo định lý Viète, ta có $x$ và $y$ là hai nghiệm của phương trình $X^2-SX+P=0$, tương đương với phương trình $X^2-2X=0$.

Phương trình $X^2-2X=0$ có hai nghiệm là $X=0$ và $X=2$.

Hệ phương trình đã cho có hai nghiệm là $(0; 2)$ và $(2; 0)$.

Cách 2:.

Lời giải:.

$\Left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right$

$\Leftrightarrow \left\{\begin{array}{ll}x&=2-y \\ (2-y)^2+y^2&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=2-y \\ 4-4y+y^2+y^2&=4\end{array}\right$.

Khi giải phương trình $2y^2-4y+4=4$, ta thu được hai nghiệm là $y=0$ và $y=2$.

Khi thay $y=0$ vào phương trình $x=2-y$, ta thu được $x=2$.

Khi thay $y=2$ vào phương trình $x=2-y$, ta thu được $x=0$.

Nghiệm của hệ phương trình đã cho là $(2; 0)$ và $(0; 2)$.

Cách 3:.

Lời giải:.

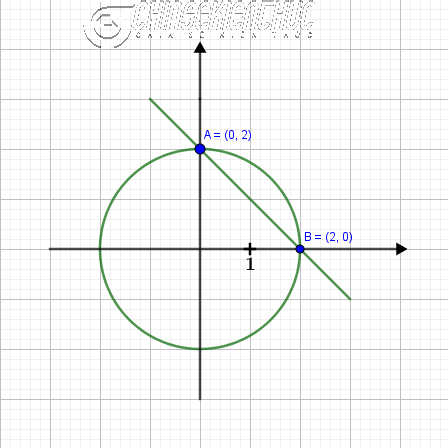
Hai đồ thị của hàm số khi được quan sát, ta có thể nhận thấy rằng chúng có hai điểm giao nhau là $A=(0; 2)$ và $B=(2; 0)$.

Dự đoán rằng $(0; 2)$ và $(2; 0)$ là nghiệm của hệ phương trình đã cho.

Khi thay $A(0; 2)$ và $B(2; 0)$ vào hệ phương trình, ta thu được ….

$\Left\{\begin{array}{ll}0+2&=2 \\ 0^2+2^2&=4\end{array}\right.$ Và $\left\{\begin{array}{ll}2+0&=2 \\ 2^2+0^2&=4\end{array}\right.$ Có thể viết lại như sau:$\left\{\begin{array}{ll}2+0&=2 \\ 2^2+0^2&=4\end{array}\right.$ Và $\left\{\begin{array}{ll}0+2&=2 \\ 0^2+2^2&=4\end{array}\right.$.

Các hệ thức trên đều chính xác.

Nghiệm của hệ phương trình đã cho là $(0; 2)$ và $(2; 0)$.

V. Lời kết

Dưới đây là 7 đẳng thức quan trọng và các đẳng thức mở rộng tương ứng.

Các đẳng thức mà tôi vừa trình bày đã được chứng minh, nếu muốn chứng minh lại, bạn có thể biến đổi vế trái thành vế phải bằng cách nhân đa thức với đa thức và rút gọn.

Mặc dù vậy, tôi không khuyến khích các bạn thực hiện hành động đó vì nó chỉ làm mất thời gian mà không mang lại lợi ích gì.

Thay thế bằng việc dành thời gian để tập luyện và làm thêm ví dụ để ghi nhớ và sử dụng thành thạo các hằng đẳng thức này. Chào tạm biệt và hẹn gặp lại trong các bài viết tiếp theo!

Nhựt Nguyễn là CTV của Blogchiasẻkiếnthức.Com.

Đoạn văn đã được viết lại: Bài viết được đánh giá 3.4/5 sao, dựa trên 7 lượt đánh giá.

Đừng bỏ qua việc đánh giá, like và chia sẻ bài viết này với bạn bè và người thân của bạn. Bạn có thấy bài viết này hữu ích không?