Hằng Đẳng Thức Đáng Nhớ – Kiến Thức Quan Trọng Cần Nhớ

Những hằng đẳng thức đáng nhớ chắc không còn xa lạ gì với các bạn . Hôm nay Kiến sẽ nói kỹ hơn về 7 hằng đẳng thức quan trọng : bình phương của một tổng, bình phương của một hiệu, hiệu của hai bình phương, lập phương của một tổng, lập phương của một hiệu, tổng hai lập phương và cuối cùng là hiệu hai lập phương. Các bạn cùng tham khảo nhé.

A. 7 hằng đẳng thức đáng nhớ

1. Bình phương của một tổng

Với A, B là các biểu thức tùy ý, ta có: ( A + B )2 = A2 + 2AB + B2.

Ví dụ:

a) Tính ( a + 3 )2. b) Viết biểu thức x2+ 4x + 4 dưới dạng bình phương của một tổng.

Hướng dẫn:

a) Ta có: ( a + 3 )2= a2+ 2.a.3 + 32 = a2 + 6a + 9. b) Ta có x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.

2. Bình phương của một hiệu

Với A, B là các biểu thức tùy ý, ta có: ( A – B )2 = A2 – 2AB + B2.

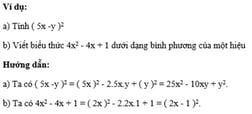
3. Hiệu hai bình phương

Với A, B là các biểu thức tùy ý, ta có: A2 – B2 = ( A – B )( A + B ).

4. Lập phương của một tổng

Với A, B là các biểu thức tùy ý, ta có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.

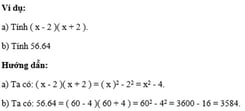
5. Lập phương của một hiệu.

Với A, B là các biểu thức tùy ý, ta có: ( A – B )3 = A3 – 3A2B + 3AB2 – B3.

Ví dụ :

a) Tính ( 2x – 1 )3. b) Viết biểu thức x3- 3x2y + 3xy2- y3 dưới dạng lập phương của một hiệu.

Hướng dẫn:

a) Ta có: ( 2x – 1 )3

= ( 2x )3 – 3.( 2x )2.1 + 3( 2x ).12 – 13

= 8×3 – 12×2 + 6x – 1

b) Ta có : x3- 3x2y + 3xy2- y3

= ( x )3 – 3.x2.y + 3.x. y2 – y3

= ( x – y )3

6. Tổng hai lập phương

Với A, B là các biểu thức tùy ý, ta có: A3 + B3 = ( A + B )( A2 – AB + B2 ).

Chú ý: Ta quy ước A2 – AB + B2 là bình phương thiếu của hiệu A – B.

Ví dụ:

a) Tính 33+ 43. b) Viết biểu thức ( x + 1 )( x2- x + 1 ) dưới dạng tổng hai lập phương.

Hướng dẫn:

a) Ta có: 33+ 43= ( 3 + 4 )( 32 – 3.4 + 42 ) = 7.13 = 91. b) Ta có: ( x + 1 )( x2- x + 1 ) = x3+ 13 = x3 + 1.

7. Hiệu hai lập phương

Với A, B là các biểu thức tùy ý, ta có: A3 – B3 = ( A – B )( A2 + AB + B2 ).

Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.

Ví dụ:

a) Tính 63- 43. b) Viết biểu thức ( x – 2y )( x2+ 2xy + 4y2) dưới dạng hiệu hai lập phương

Hướng dẫn:

a) Ta có: 63- 43= ( 6 – 4 )( 62 + 6.4 + 42 ) = 2.76 = 152. b) Ta có : ( x – 2y )( x2+ 2xy + 4y2) = ( x )3 – ( 2y )3 = x3 – 8y3.

B. Bài tập tự luyện về hằng đẳng thức

Bài 1.Tìm x biết

a) ( x – 3 )( x2+ 3x + 9 ) + x( x + 2 )( 2 – x ) = 0. b) ( x + 1 )3- ( x – 1 )3- 6( x – 1 )2 = – 10.

Hướng dẫn:

a) Áp dụng các hằng đẳng thức ( a – b )( a2+ ab + b2) = a3 – b3.

( a – b )( a + b ) = a2 – b2.

Khi đó ta có ( x – 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.

⇔ x3 – 33 + x( 22 – x2 ) = 0 ⇔ x3 – 27 + x( 4 – x2 ) = 0

⇔ x3 – x3 + 4x – 27 = 0

⇔ 4x – 27 = 0

Vậy x= .

b) Áp dụng hằng đẳng thức ( a – b )3= a3- 3a2b + 3ab2 – b3

( a + b )3 = a3 + 3a2b + 3ab2 + b3

( a – b )2 = a2 – 2ab + b2

Khi đó ta có: ( x + 1 )3 – ( x – 1 )3 – 6( x – 1 )2 = – 10.

⇔ ( x3 + 3×2 + 3x + 1 ) – ( x3 – 3×2 + 3x – 1 ) – 6( x2 – 2x + 1 ) = – 10

⇔ 6×2 + 2 – 6×2 + 12x – 6 = – 10

⇔ 12x = – 6

Vậy x=

Bài 2: Rút gọn biểu thức A = (x + 2y ).(x – 2y) – (x – 2y)2

1. 2×2+ 4xy B. – 8y2+ 4xy
2. – 8y2 D. – 6y2+ 2xy

Hướng dẫn

Ta có: A = (x + 2y ). (x – 2y) – (x – 2y)2

A = x2 – (2y)2 – [x2 – 2.x.2y +(2y)2 ]

A = x2 – 4y2 – x2 + 4xy – 4y22

A = -8y2 + 4xy

• Hãy nhớ nó nhé

Những hằng đẳng thức đáng nhớ trên rất quan trọng tủ kiến thức của chúng ta . Thế nên các bạn hãy nghiên cứu và ghi nhớ nó nhé. Những đẳng thức đó giúp chúng ta xử lý các bài toán dễ và khó một cách dễ dàng, các bạn nên làm đi làm lại để bản thân có thể vận dụng tốt hơn. Chúc các bạn thành công và chăm chỉ trên con đường học tập. Hẹn các bạn ở những bài tiếp theo