Các bài tập về nhị thức Newton là bài toán quan trọng trong đề thi trung học phổ thông Quốc Gia. Chuyên đề này giúp học sinh nắm chắc dạng bài tập về: tính tổng, rút gọn biểu thức, tìm hệ số và số hạng trong khai triển lũy thừa thông qua các ví dụ.
NHỊ THỨC NEWTON
I)KIẾN THỨC CẦN NHỚ:
1. Hoán vị:
({P_n} = n.(n – 1).(n – 2)…3.2.1)
2. Chỉnh hợp:
(A_n^k = frac{{left( {n – k} right)!}}{{k!}} = n.(n – 1)…(n – k + 1))
3. Tổ hợp:
(C_n^k = frac{{n!}}{{k!(n – k)!}} = frac{{n.(n – 1)…(n – k + 1)}}{{k!}})
*) Tính chất: (C_n^k = C_n^{n – k})
(C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1})
4. Công thức Newton:
({left( {a + b} right)^n} = sumlimits_{k = 0}^n {C_n^k} {a^{n – k}}{b^k} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + C_n^2{a^{n – 2}}{b^2} + … + C_n^n{b^n})
({left( {a – b} right)^n} = {left( { – 1} right)^n}sumlimits_{k = 0}^n {C_n^k} {a^{n – k}}{b^k} = C_n^0{a^n} – C_n^1{a^{n – 1}}b + C_n^2{a^{n – 2}}{b^2} – … + {left( { – 1} right)^n}C_n^n{b^n})
II) CÁC DẠNG BÀI TẬP:
Dạng 1: Phương trình, bất phương trình chỉnh hợp tổ hợp.

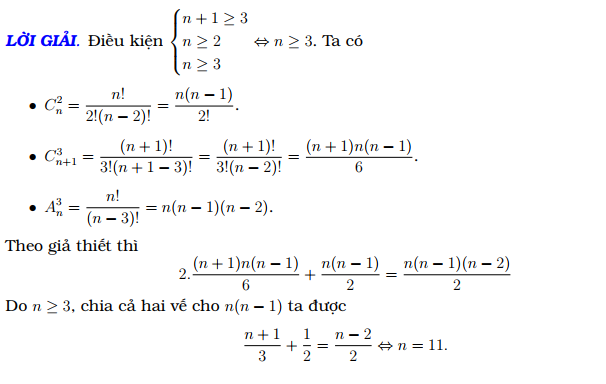

Dạng 2: Rút gọn đẳng thức, chứng minh biểu thức.



Dạng 3: Xác định hệ số, số hạng trong khai triển lũy thừa.




III)BÀI TẬP RÈN LUYỆN:




Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Tải về
Luyện Bài tập trắc nghiệm môn Toán lớp 11 – Xem ngay

Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!
