Bát diện đều: Công thức tính thể tích và bài tập

Bát diện đều là một khái niệm trong hình học. Để hiểu về bát diện đều, chúng ta cần nắm vững các tính chất và công thức liên quan. Dưới đây, tôi sẽ giới thiệu đến các bạn những tính chất và công thức này. Hãy cùng theo dõi bài viết để tìm hiểu chi tiết.

II. THỂ TÍCH BÁT DIỆN ĐỀU

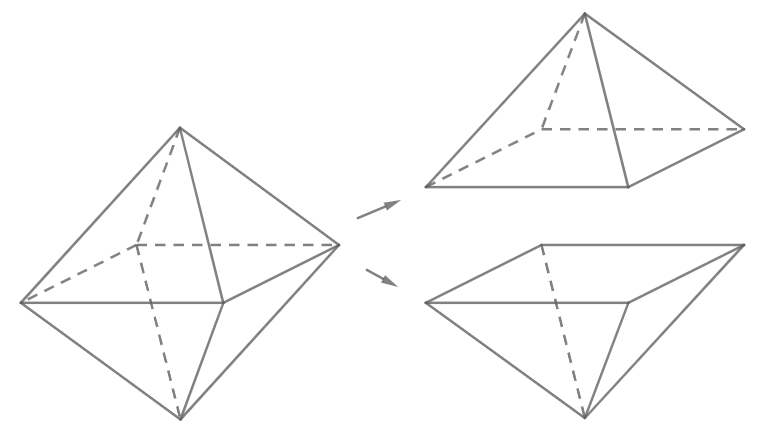
Có thể phân chia khối bát diện đều thành hai khối chóp tứ giác đều, mỗi khối chóp có các cạnh bằng nhau và hai khối chóp này cũng bằng nhau.

Nhưng chúng ta đã biết rằng khối chóp tứ giác đều có tất cả các cạnh bằng a có thể tích là.

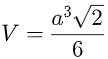
Do vậy công thức tính thể tích của khối bát diện đều có cạnh đồng đều bằng a là.

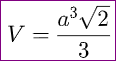
I. HÌNH BÁT DIỆN ĐỀU

Hình bát diện đều là một loại hình đa diện đều có 3 cạnh. Điều này có nghĩa là mỗi mặt của hình là một tam giác đều và mỗi đỉnh của hình là điểm giao của chính xác 4 mặt.

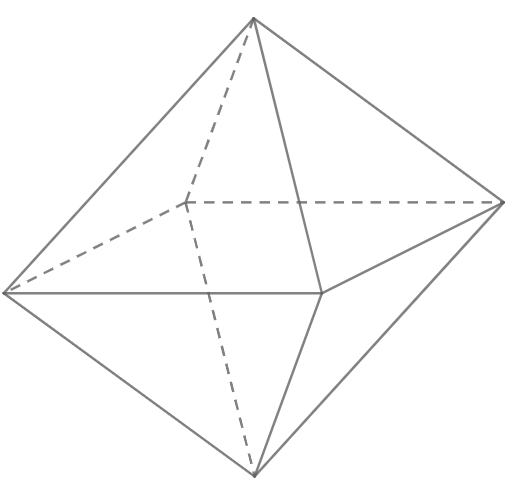
Chúng ta có thể thấy rằng hình/khối bát có 6 đỉnh, 12 cạnh, 8 bề mặt và 9 mặt phẳng đối xứng.

Về vấn đề các mặt phẳng đối xứng của bát đều. Ban đầu, tôi không có ý định vẽ và liệt kê ở đây. Tuy nhiên, sau khi xem qua nhiều hình vẽ sai trên mạng và lại xuất hiện trong kết quả tìm kiếm hàng đầu của Google, tôi quyết định vẽ lại để các bạn có thể dễ dàng theo dõi.

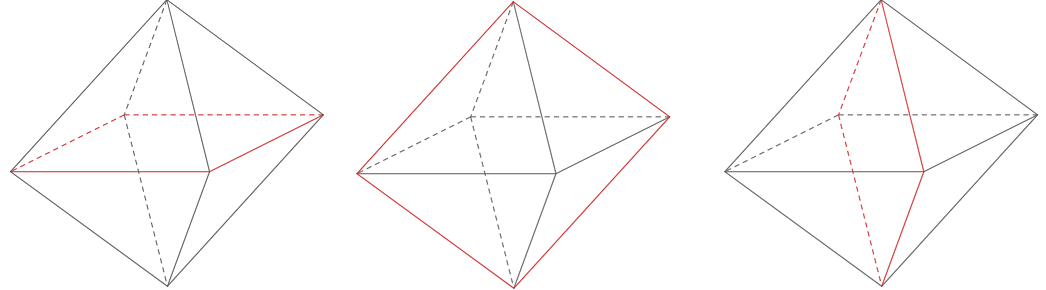
Đầu tiên chúng ta có 3 mặt phẳng chứa các hình vuông của bát đều (đi qua 4 đỉnh).

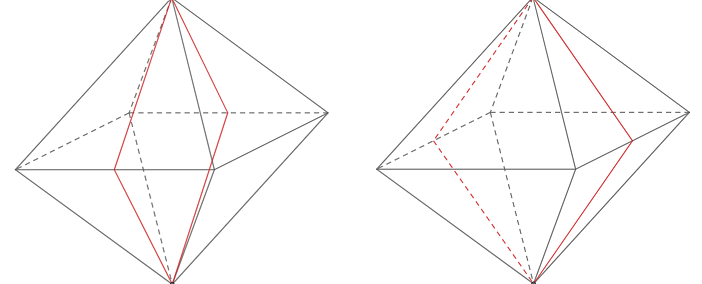
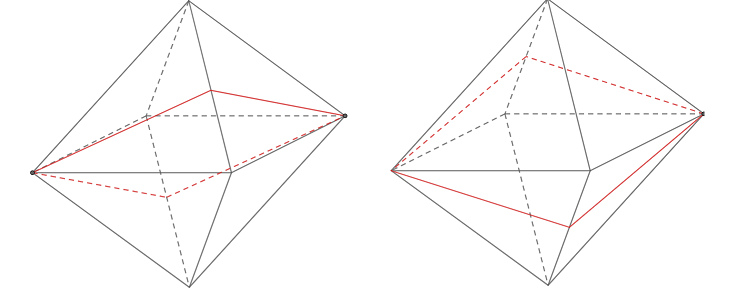
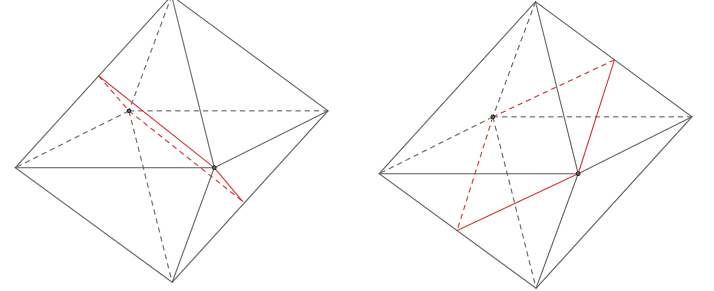
Tiếp theo, mỗi cặp đỉnh đối nhau của bát diện sẽ được kết nối bởi hai mặt phẳng đối xứng (đi qua hai đỉnh).

Cặp đỉnh trên và cặp đỉnh dưới.

Cặp đỉnh bên trái và bên phải.

Cặp đỉnh trước và sau.

III. DIỆΝ TÍCH BÁT DΙỆΝ ĐỀU

Tổng diện tích của hình bát diện đều, với các mặt là các tam giác đều có cạnh bằng a, là.

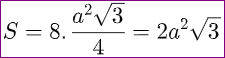
Các bạn nhận được một số công thức và tính chất liên quan đến hình bát diện đều từ toanthaydinh.Com. Chúc các bạn học tốt và đạt được thành công!

Công thức tính nhanh tỷ lệ thể tích khối đa diện.

Thể tích tứ diện đều: Khái niệm, công thức và bài tập cụ thể.