Toán học là một môn học không thể thiếu trong toàn bộ quá trình giảng dạy từ cấp tiểu học đến trung học phổ thông tại Việt Nam. Những kiến thức về toán học luôn rất cực kỳ đa dạng và phong phú. Trong bài viết này, chúng tôi sẽ trình bày về chủ đề này trên trang web sentayho.Com.Vn.
Các thắc mắc về số nguyên và số thực sẽ được giải đáp. Cung cấp ví dụ và các tính chất của số nguyên.
Bạn đang xem: Ý nghĩa của số nguyên dương là gì?
Số nguyên là một khái niệm rất rộng, bao gồm số 0 và tập hợp các số tự nhiên dương và số tự nhiên âm. Tập hợp số nguyên được kí hiệu là Z và có tính chất cơ bản là vô hạn và có thể đếm được.

Khái niệm về số nguyên không có giới hạn về số lớn nhất hay nhỏ nhất. Số nguyên dương nhỏ nhất là 1 và số nguyên âm nhỏ nhất là -1. Một tập con hữu hạn bất kỳ của tập số nguyên Z luôn có phần tử lớn nhất và phần tử nhỏ nhất. Không tồn tại bất kỳ số nguyên nào nằm giữa hai số nguyên liền kề.
Số nguyên được chia thành hai loại là số nguyên âm và số nguyên dương. Số nguyên dương là kết quả của câu hỏi “số tự nhiên là gì”. Theo lý thuyết, số nguyên dương là những số lớn hơn 0. Số tự nhiên bao gồm số 0 và các số nguyên dương. Do đó, số nguyên dương là một phần của số tự nhiên. Tập hợp Z+ là tập số nguyên dương.
Ví dụ, số nguyên là gì?
Số nguyên âm là tập hợp các số nguyên nhỏ hơn 0 (không bao gồm số 0) và được kí hiệu là Z-.
Đầu vào: Số thực là gì? Q là tập hợp số gì?Đầu ra: Số thực có nghĩa là gì? Q đại diện cho tập hợp số nào?
Số thực không giống số nguyên vì nó không thể được đếm. Số thực bao gồm số nguyên, số hữu tỉ và số vô tỉ. Số nguyên là một phần của số thực. Số thực có thể được hiểu như các điểm trên một trục số dài vô hạn. Kí hiệu của tập hợp số thực là R.
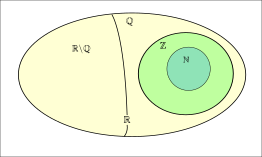
Đầu vào: Số thực là gì? Q là tập hợp số gì?Đầu ra: Số thực có nghĩa là gì? Q đại diện cho tập hợp số nào?
Tính chất của số thực được xây dựng dựa trên tính chất của các số tạo nên nó, bao gồm số nguyên, số hữu tỉ và số vô tỉ. Có những người thắc mắc về tập hợp Q trong R. Thực chất, Q là tập hợp các số hữu tỉ. Sự khác biệt lớn nhất giữa số nguyên và số thực là ở khái niệm của hai loại số này, với số nguyên chỉ là một tập con của số thực.
Bài viết này tổng hợp những khái niệm cơ bản về số nguyên và số thực. Chúng tôi hy vọng rằng bạn sẽ luôn hiểu rõ những kiến thức này để vượt qua môn Toán học.

Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!
