Mẹo hay Top cách bấm máy tính tiệm cận [Hot Nhất 2023]

Bài toán tìm tiệm cận hàm số sau: Số tiệm cận đứng của đồ thị hàm số [latex]frac{sqrt{x+9}-3}{{{x}^{2}}+x}[/latex] là:

1. 3
2. 2
3. 0
4. 1

(Trích câu 18 – Mã đề 101 đề thi THPTQG 2018)

Lời giải tự luận

Ta nhắc lại về định nghĩa tiệm cận đứng, đường thẳng $latex x={{x}_{0}}$ được gọi là đường tiệm cận đứng của đồ thị hàm số $latex y=f(x)$ nếu ít nhất một trong các điều kiện sau được thoả mãn:

$latex underset{xto x_{0}^{-}}{mathop{lim }},f(x)=+infty \ underset{xto x_{0}^{-}}{mathop{lim }},f(x)=-infty \ underset{xto x_{0}^{+}}{mathop{lim }},f(x)=+infty \ underset{xto x_{0}^{+}}{mathop{lim }},f(x)=-infty$

Quay trở lại bài toán trên, ta có tập xác định của $latex f(x)$ là: $latex D=[-9;+infty )backslash {0;1}$.

Ta có: $latex underset{xto -{{1}^{+}}}{mathop{lim }},dfrac{sqrt{x+9}-3}{{{x}^{2}}+x}=+infty$ nên $latex x=-1$ là tiệm cận đứng

Mặc khác:

$latex begin{align} & underset{xto 0}{mathop{lim }},dfrac{sqrt{x+9}-3}{{{x}^{2}}+x} \ & =underset{xto 0}{mathop{lim }},dfrac{left( sqrt{x+9}-3 right)left( sqrt{x+9}+3 right)}{left( {{x}^{2}}+x right)left( sqrt{x+9}+3 right)} \ & =underset{xto 0}{mathop{lim }},dfrac{x+9-9}{left( {{x}^{2}}+x right)left( sqrt{x+9}+3 right)} \ & =underset{xto 0}{mathop{lim }},dfrac{1}{left( x+1 right)left( sqrt{x+9}+3 right)} \ & =dfrac{1}{6} \ end{align}$

Nên $latex x=0$ không phải là tiệm cận đứng.

Vậy chỉ có 1 đường tiệm cận đứng do đó ta chọn đáp án D.

Chúng ta có thể xác định nhanh giới hạn của $latex f(x)$ bằng máy tính cầm tay CASIO fx 580VNX như sau:

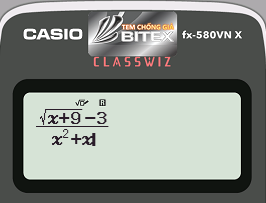
Bước 1: Nhập biểu thức $latex f(x)$

• Cách bấm: as[+9$p3R[d+[
• Máy tính hiển thị:

Bước 2: Để tính $latex underset{xto -{{1}^{+}}}{mathop{lim }},frac{sqrt{x+9}-3}{{{x}^{2}}+x}$ ta có thể CALC tại giá trị $latex x=-1+{{10}^{-6}}approx -1$

• Cách bấm: as[+9$p3R[d+[==
• Máy tính hiển thị:

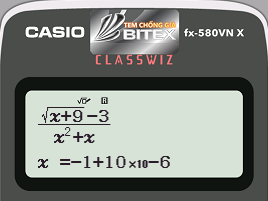
Từ kết quả ta dự đoán $latex underset{xto -{{1}^{+}}}{mathop{lim }},dfrac{sqrt{x+9}-3}{{{x}^{2}}+x}=+infty$ nên $latex x=-1$ là một tiệm cận đứng.

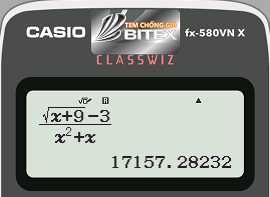
Bước 3: Để tính $latex underset{xto 0}{mathop{lim }},dfrac{sqrt{x+9}-3}{{{x}^{2}}+x}$ ta có thể CALC tại giá trị $latex x=0+{{10}^{-6}}approx 0$

• Cách bấm: !r0+10Kp6==
• Máy tính hiển thị:

Từ kết quả ta dự đoán $latex underset{xto -{{1}^{+}}}{mathop{lim }},dfrac{sqrt{x+9}-3}{{{x}^{2}}+x}=0,1666649544approx dfrac{1}{6}$ nên $latex x=0$ không là một tiệm cận đứng.

Các bạn tham khảo đồ thị của hàm số và đường tiệm cận đứng qua hình sau:

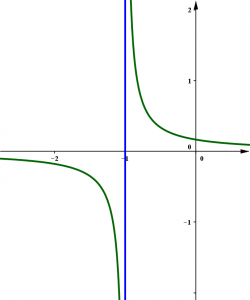
Trên đây diendanmaytinhcamtay.vn đã giới thiệu cho các bạn cách tìm tiệm cận đứng để giải bài toán tìm tiệm cận hàm số trong đề thi THPTQG 2018. Truy cập diễn đàn mỗi ngày để xem thêm nhiều bài toán ứng dụng hay về cách sử dụng máy tính cầm tay CASIO fx 580VNX.