Góc đồng vị là gì? Góc đồng vị, góc so le trong, góc cùng phía?

Trong hình học, góc là một đối tượng hình học được định nghĩa với hai tia có điểm cuối chung. Hai tia này được gọi là tâm của góc còn điểm cuối chung của chúng được cho là đỉnh của nó. Các góc này được xác định nằm trên mặt phẳng Euclide, tuy nhiên một số góc cũng có thể được phân biệt trong hình học Euclid. Góc có nhiều ứng dụng trong hình học và nghệ thuật. Dưới bày viết sau đây chúng tôi sẽ đi vào tìm hiểu một nội dung về góc đó là “Góc đồng vị”

1. Góc đồng vị là gì?

1.1. Định nghĩa và tính chất của 2 góc đồng vị:

Nếu đường thẳng t cắt hai đường thẳng f và r và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc đồng vị khác cũng bằng nhau

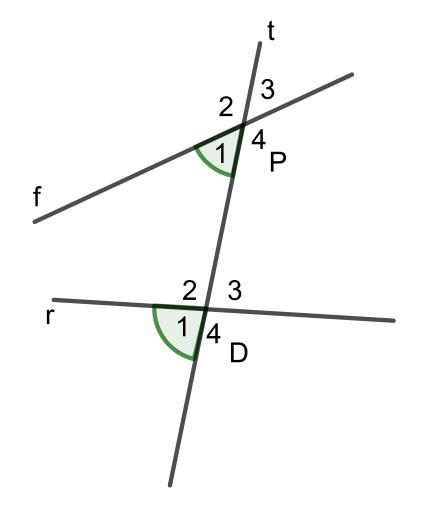
Hai góc P1 và D1 được gọi là hai góc đồng vị

Ta có thể hiểu hai góc đồng vị là hai góc nằm ở vị trí giống nhau.

Có thể rút ra dấu hiệu cơ bản để nhận biết mối quan hệ góc này là:

– Hai góc không chung gốc.

– Hai góc nằm ở cùng một phía so với đường thẳng cắt và nằm ở vị trí giống nhau trên 2 đường thẳng song song.

Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

– Hai góc so le trong còn lại bằng nhau

– Hai góc đồng vị bằng nhau

1.2. Phương pháp nhận biết hai góc đồng vị:

Để nhận biết hai góc đồng vị, ta dựa vào những dấu hiệu sau đây:

Cho đường thẳng A cắt hai đường thẳng B và C tạo thành các góc. Khi đó các cặp góc đồng vị có những đặc điểm sau:

Thứ nhất, Hai góc không được chung gốc

Thứ hai, Hai góc đó phải nằm cùng một phía so với đường thẳng A và nằm ở vị trí giống nhau trên hai đường thẳng B và C

1.3. Các dạng bài tập về góc đồng vị:

Dạng bài tập 1: Nhận biết hai góc đồng vị. Phương pháp giải của dạng bài tập này là dựa vào định nghĩa góc đồng vị.

Dạng bài tập 2: Tính số đo của các góc tạo thành từ một đường thẳng cắt hai đường thẳng song song. Phương pháp giải của dạng bài tập này là áp dụng các tính chất của góc đồng vị (hai góc đồng vị bằng nhau) để tìm ra hướng tính toán hợp lý.

Dạng bài tập 3: Chứng minh hai đường thẳng song song. Dựa vào định lý đảo góc đồng vị, nếu như một đường thẳng cắt hai đường thẳng bất kì, hai góc ở vị trí đồng vị bằng nhau thì chứng tỏ hai đường thẳng đó song song.

2. Góc so le trong là gì?

2.1. Góc so le trong là gì?

Định nghĩa góc so le trong: Giả sử có một đường thẳng t cắt đường thẳng q tạo thành bốn góc và cắt đường thẳng r tạo thành bốn góc. Khi đó hai góc so le trong là hai góc không chung đỉnh, nằm ở bên trong hai đường thẳng q và r và nằm ở khác phía so với đường thẳng t.

Ví dụ:

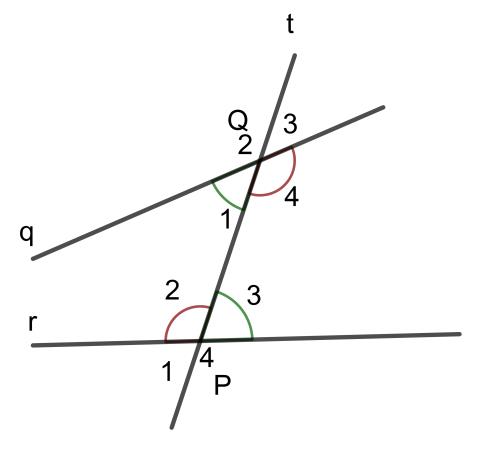
Góc Q1 và góc P3 là hai góc so le trong

Tương tự, góc Q4 và góc P2 là hai góc so le trong

2.2 Tính chất:

Nếu đường thẳng cc cắt hai đường thẳng aa và bb, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

a) Hai góc so le trong còn lại bằng nhau.

b) Hai góc đồng vị (trong mỗi cặp) bằng nhau.

c) Hai góc trong cùng phía bù nhau

Cụ thể như sau:

Từ hình vẽ trên, ta thấy các góc Q3, Q4, P1, P2 là các góc nằm ở phía trong hai đường thẳng u và v.

Góc Q1 và P3 là hai góc không chung gốc, nằm ở khác phía so với đường thẳng t nên góc P1 và T3 là hai góc so le trong.

Tương tự, ta có góc Q4 và P2 là hai góc không chung gốc, nằm ở khác phía so với đường thẳng t nên góc Q4 và P2 là hai góc so le trong.

Còn góc Q1 và P2, Q4 và P3 cũng là các cặp góc không chung gốc nhưng nằm cùng một phía với đường thẳng q nên các cặp góc đó không phải là góc so le trong.

2.3. Dấu hiệu nhận biết hai góc so le trong:

Cho đường thẳng t cắt hai đường thẳng q và r tạo thành các góc. Khi đó để nhận biết được hai góc so le trong, ta dựa vào các dấu hiệu sau:

Dấu hiệu 1: Hai góc không được chung gốc

Dấu hiệu 2: Hai góc đó phải nằm ở phía trong hai đường thẳng q và r.

Dấu hiệu 3: Hai góc đó phải nằm ở vị trí so le nhau, hay nói cách khác, hai góc đó phải nằm ở khác phía so với đường thẳng t.

3. Góc cùng phía là gì?

3.1. Định nghĩa:

Giả sử có một đường thẳng d bất kì cắt đường thẳng q và t tạo thành các góc. Khi đó hai góc trong cùng phía là hai góc không chung đỉnh, nằm ở phía bên trong hai đường thẳng q và t và nằm ở cùng một phía so với đường thẳng d.

Nhận xét: Nếu đường thẳng d cắt hai đường thẳng q và t mà q và t song song với nhau thì các góc trong cùng phía sẽ bù nhau. Khi đó tổng số đo của hai góc trong cùng phía sẽ bằng 180o.

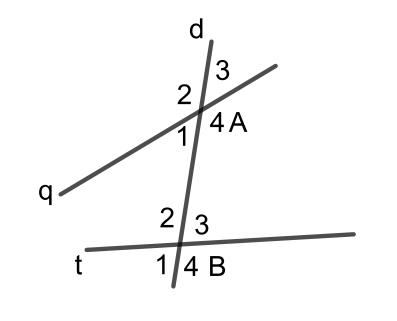
Từ hình vẽ trên, ta thấy góc A1 và góc B2 là hai góc trong cùng phía.

Tương tự như vậy, ta cũng có góc A4 và B3 là hai góc trong cùng phía.

3.2. Cách nhận biết góc trong cùng phía:

Giả sử có một đường thẳng d cắt đường thẳng q tại B và cắt đường thẳng t tại F tạo thành các góc đỉnh B và đỉnh F. Khi đó để biết được hai góc như thế nào là hai góc trong cùng phía ta dựa vào các đặc điểm sau:

– Hai góc đó không chung gốc. Có nghĩa là một góc đỉnh B và một góc đỉnh F.

– Hai góc đó đều nằm ở phía trong so với hai đường thẳng q và t.

– Hai góc đó nằm ở vị trí cùng một bên so với đường thẳng d. Hay nói cách khác, hai góc đó phải nằm ở cùng phía so với đường thẳng d.

4. Các dạng bài tập thường gặp:

– Dạng 1: Xác định các cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía.

– Dạng 2: Tính số đo góc khi biết một trong bốn góc tạo bởi hai đường thẳng.

– Dạng 3: Tìm các cặp góc bằng nhau, cặp góc bù nhau.

– Dạng 4: Xác định vị trí của các góc.

– Dạng 5: Chứng minh vị trí của các góc.

– Dạng 6: Tìm các cặp góc thỏa mãn điều kiện bài cho.

– Dạng 7: Ứng dụng vị trí của góc vào các bài toán khác: tam giác, hình vuông, hình tròn.

5. Phương pháp giải các bài tập về góc và ví dụ minh họa:

Để giải tốt bài toán tính số đo góc thì người học trước hết phải nắm vững kiến thức cơ bản sau về góc và các mối quan hệ trong góc như sau:

* Trong tam giác:

+ Tổng ba góc trong bằng 180°.

+ Khi biết hai góc chúng ta xác định được góc còn lại.

* Trong tam giác cân: Biết một góc chúng ta xác định được hai góc còn lại.

* Trong tam giác vuông:

+ Biết một góc nhọn, chúng ta xác định được góc nhọn còn lại.

+ Cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông đó có số đo bằng 30°30°.

* Trong tam giác vuông cân: Mỗi góc nhọn có số đo bằng 45°45°.

* Trong tam giác đều: Mỗi góc có số đo bằng 60°.60°.

* Đường phân giác của một góc chia góc đó ra hai góc có số đo bằng nhau.

* Hai đường phân giác của hai góc kề bù thì vuông góc với nhau.

* Hai góc đối đỉnh thì bằng nhau.

* Tính chất về góc so le trong, đồng vị, trong cùng phía, của một đường thẳng cắt hai đường thẳng song song.

Trong thực tế, để giải bài toán tính số đo góc, ta thường xét các góc đó nằm trong mối liên hệ với các góc ở các hình đặc biệt đã nêu ở trên hoặc xét các góc tương ứng bằng nhau,. .. rồi sau đó sẽ suy được ra kết quả.

Ví dụ minh họa 1: Nếu hai đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

A. Hai góc trong cùng phía bằng nhau

B. Hai góc đồng vị bằng nhau

C. Hai góc so le trong còn lại có tổng bằng 120°

D. Tất cả các đáp án trên đều đúng

Đáp án cần chọn là: B

Nếu đường thẳng c cắt hai đường thẳng a, và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: hai góc đồng vị bằng nhau

Ví dụ minh họa số 2: Nếu hai đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì:

A. Hai góc trong cùng phía bằng nhau

B. Hai góc so le trong bù nhau

C. Hai góc trong cùng phía bù nhau

D. Tất cả các đáp án trên đều đún

Đáp án cần chọn là: C

Đường thẳng c cắt hai đường thẳng a,b tương ứng tại A,B và trong các góc tạo thành có một cặp góc đồng vị bằng nhau, giả sử

+ Xét một cặp góc trong cùng phía, chẳng hạn

Do đó hai góc trong cùng phía bù nhau nên A sai, C đúng

Vậy hai góc so le trong bằng nhau. Đáp án B sai