Chia sẻ cách tính khoảng cách từ một điểm đến một mặt phẳng trong hình học không gian trong hệ tọa độ Oxyz, kiến thức Toán 11.
Phương pháp tính khoảng cách từ: Điểm ${M_0}left( {{x_0};{y_0};{z_0}} right)$ tới mặt phẳng $(alpha ):ax + by + cz + d = 0.$
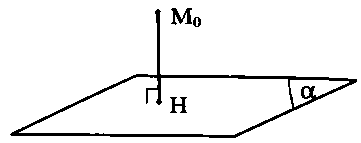
Công thức: $dleft( {{M_0};(alpha )} right) = frac{{left| {a{x_0} + b{y_0} + c{z_0} + d} right|}}{{sqrt {{a^2} + {b^2} + {c^2}} }}.$
Hệ quả:
* ${M_0} in (alpha )$ $ Leftrightarrow dleft( {{M_0};(alpha )} right) = 0.$
* $ dleft( {{{M}_{0}};(alpha )} right)$ với $left{begin{array}{l}M_{0} H perp(alpha) \ H in(alpha)end{array}right.$
* Với mọi $M in (alpha ):$ $dleft( {{M_0};(alpha )} right) le {M_0}M.$
Bài tập tính khoảng cách từ một điểm đến mặt phẳng
Câu 1: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ $A(1;2;3)$ đến mặt phẳng $(Oxy).$
A. $d=1.$
B. $d=2.$
C. $d=3.$
D. $d = sqrt 5 .$
Lời giải:
Mặt phẳng $(Oxy)$ có phương trình: $z = 0.$
$ Rightarrow d(A;(Oxy)) = frac{{|3|}}{{sqrt 1 }} = 3.$
Chọn đáp án C.
Câu 2: Trong không gian với hệ tọa độ $Oxyz$, gọi $A’$ là điểm đối xứng của điểm $A(1;2;3)$ qua mặt phẳng $(Oxy).$ Tính độ dài đoạn thẳng $AA’.$ A. $4.$ B. $2.$ C. $3.$ D. $6.$
Lời giải:
Mặt phẳng $(Oxy)$ có phương trình: $z = 0$ $ Rightarrow d(A;(Oxy)) = frac{{|3|}}{{sqrt 1 }} = 3.$
Suy ra: $AA’ = 2d(A;(Oxy)) = 6.$
Chọn đáp án D.
Kết quả lưu ý: Với $left( {{x_0};{y_0};{z_0}} right)$ ta có:
$d(M;(Oxy)) = left| {{z_0}} right|.$
$d(M;(Oyz)) = left| {{x_0}} right|.$
$d(M;(Oxz)) = left| {{y_0}} right|.$
Câu 3: Trong không gian với hệ tọa độ $Oxyz$, gọi $H$ là hình chiếu vuông góc của $A(1;2;-3)$ trên mặt phẳng $(Oxy).$ Tính diện tích $S$ tam giác $OHA.$
A. $S = frac{{sqrt {13} }}{2}.$
B. $S = sqrt {10} .$
C. $S = frac{{3sqrt 5 }}{2}.$
D. $S = frac{{5sqrt {15} }}{2}.$
Lời giải:
Ta có: $OA = sqrt {14} $, $AH = d(A;(Oxy)) = 3.$
Tam giác $OHA$ vuông tại $H$ suy ra: $OH = sqrt {O{A^2} – A{H^2}} = sqrt 5 .$
Vậy $S = frac{1}{2}AH.OH = frac{{3sqrt 5 }}{2}.$
Chọn đáp án C.
Câu 4: Trong không gian với hệ tọa độ $Oxyz$, gọi $H$ là hình chiếu vuông góc của $A(1;2;-3)$ trên mặt phẳng $(Oxz).$ Tính diện tích $S$ tam giác $OHA.$
A. $S = frac{{sqrt {13} }}{2}.$
B. $S = sqrt {10} .$
C. $S = frac{{3sqrt 5 }}{2}.$
D. $S = frac{{5sqrt {15} }}{2}.$
Lời giải:
Ta có: $OA = sqrt {14} $, $AH = d(A;(Oyz)) = 2.$
Tam giác $OHA$ vuông tại $H$ suy ra: $OH = sqrt {O{A^2} – A{H^2}} = sqrt {10} .$
Vậy $S = frac{1}{2}AH.OH = sqrt {10} .$
Chọn đáp án B.
Câu 5: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ $A(1;3;-2)$ đến mặt phẳng $(P):x + 2y – 2z + 1 = 0.$
A. $d=4.$
B. $d=2.$
C. $d=3.$
D. $d = sqrt 5 .$
Lời giải:
Ta có: $d(A;(P)) = frac{{|1 + 6 + 4 + 1|}}{{sqrt {{1^2} + {2^2} + {{( – 2)}^2}} }} = 4.$
Chọn đáp án A.
Câu 6: Trong không gian với hệ tọa độ $Oxyz$, tính bán kính $R$ của mặt cầu tâm $A(1;3;2)$ và tiếp xúc với mặt phẳng $(P):x + 2y + 2z + 1 = 0.$ A. $d=4.$ B. $d=2.$ C. $d=3.$ D. $d = sqrt 5 .$
Lời giải:
Do mặt cầu tâm $A$ tiếp xúc với mặt phẳng $(P):$
$ Leftrightarrow R = d(A;(P))$ $ = frac{{|1 + 6 + 4 + 1|}}{{sqrt {{1^2} + {2^2} + {{( – 2)}^2}} }} = 4.$
Chọn đáp án A.
Câu 7: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1;1;-2)$ và mặt phẳng $(P):2x+2y+z+1=0.$ Gọi $M$ là điểm bất kì thuộc $(P)$, tính độ dài nhỏ nhất của đoạn thẳng $AM.$
A. $2.$
B. $1.$
C. $sqrt 2 .$
D. $sqrt 3 .$
Lời giải:
Gọi $H$ là hình chiếu vuông góc của $A$ trên $(P).$
Ta có: $AM ge AH$ $ Rightarrow A{M_{min }} = AH = d(A;(P)) = 1.$
Chọn đáp án B.
Ví dụ 8: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $K(1;1;0)$ và mặt phẳng $(alpha ):x + y + z – 1 = 0.$ Gọi $(C)$ là đường tròn giao tuyến của mặt cầu tâm $K$, bán kính $R=2$ với mặt phẳng $(alpha )$, tính diện tích $S$ của $(C).$
A. $S = frac{{22pi }}{3}.$
B. $S = frac{{44pi }}{3}.$
C. $S = frac{{sqrt {33} pi }}{3}.$
D. $S = frac{{11pi }}{3}.$
Lời giải:
Ta có: $d(K;(alpha )) = frac{{sqrt 3 }}{3}.$ Gọi $r$ là bán kính đường tròn $(C)$, ta có: $r = sqrt {{R^2} – {{[d(K;(alpha ))]}^2}} = frac{{sqrt {33} }}{3}.$
Vậy $S = pi {r^2} = frac{{11pi }}{3}.$
Chọn đáp án D.
Tin tức – Tags: công thức, hình học không gian, khoảng cách, mặt phẳng
-
Các bước khảo sát và vẽ đồ thị hàm số
-
Chứng minh các BĐT về tổng, tích của dãy số bằng phương pháp làm trội, làm giảm, phương pháp quy nạp
-
Ví dụ tính tích phân hàm số lượng giác có lời giải
-
Cách tính Tích phân hàm số hữu tỷ
-
Hà Nội quyết định bỏ môn thi thứ 4 tuyển sinh lớp 10 năm học 2020 – 2021
-
60 từ vựng tiếng Anh lớp 3 có phiên âm đầy đủ
-
Những câu thơ về cha mẹ hay và ý nghĩa

Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!
