Hàm số trùng phương là một trong những dạng hàm số quan trọng. Vậy hàm trùng phương là gì? Thế nào là hàm trùng phương có 3 cực trị? Khảo sát hàm trùng phương ? Công thức cực trị của hàm trùng phương?… Trong bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề trên, cùng tìm hiểu nhé!
Hàm trùng phương là gì?
Hàm số trùng phương là hàm số bậc 4 có dạng
( y=f(x) = ax^4+bx^2+c )
Như vậy có thể coi đây là một hàm số bậc 2 với ẩn là ( x^2 )
Khảo sát hàm trùng phương
Các bước khảo sát hàm số trùng phương ( y=f(x) = ax^4+bx^2+c ) như sau:
- Tập xác định (D=mathbb{R})
- Xét chiều biến thiên
Đạo hàm ( y’= 4ax^3+2bx )
(y’=0 Leftrightarrow 2x(2ax^2+b)=0)
(Leftrightarrow left[begin{array}{l}x=0\x=pm sqrt{-frac{b}{2a}}end{array}right.)
- Tìm cực trị:
Hàm số có ( 1 ) điểm cực trị tại (x=0 Leftrightarrow ab geq 0)
Hàm số có ( 3 ) điểm cực trị tại (x=0;x=pm sqrt{-frac{b}{2a}}Leftrightarrow ab <0)
- Tìm các giới hạn vô cực:
(lim_{xrightarrow -infty}f(x)= lim_{xrightarrow +infty}f(x)=+infty Leftrightarrow a>0)
(lim_{xrightarrow -infty}f(x)= lim_{xrightarrow +infty}f(x)=-infty Leftrightarrow a<0)
- Lập bảng biến thiên:
Gồm có 3 dòng ( x; y’ ; y )
- Đồ thị hàm trùng phương

Ví dụ:
Khảo sát hàm số ( y= x^4-4x^2 +5 )
Cách giải:
Tập xác định (D=mathbb{R})
Giới hạn vô cực
(lim_{xrightarrow -infty}y=+infty)
(lim_{xrightarrow +infty}y=+infty)
Đạo hàm:
(y’=4x^3-8x=4x(x^2-2))
(y’=0Leftrightarrow left[begin{array}{l}x=0\x=pm sqrt{2}end{array}right.)
Ta có bảng biến thiên:
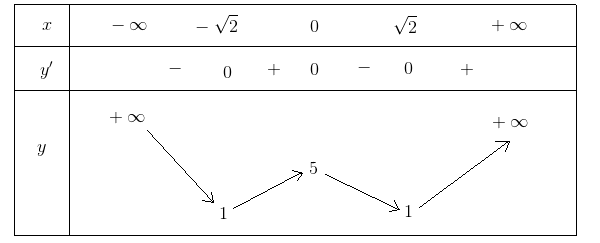
Hàm số đồng biến trên ((-sqrt{2};0)) và ((sqrt{2};+infty))
Hàm số nghịch biến trên ((-infty;-sqrt{2})) và ((0;sqrt{2}))
Hàm số có một cực đại tại ((0;5)) và hai điểm cực tiểu tại ((-sqrt{2};1);(sqrt{2};1))
Đồ thị hàm số:
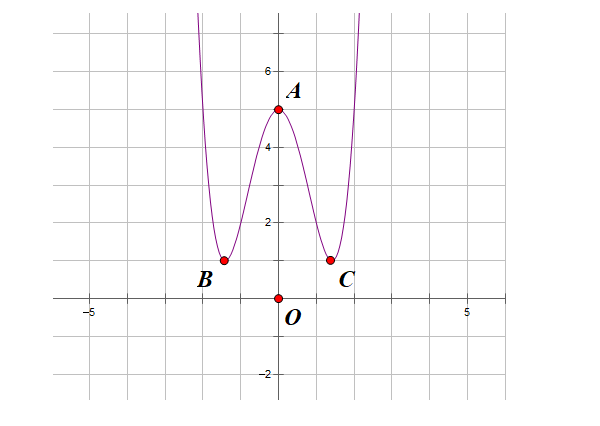
Nghiệm của hàm trùng phương
Cho hàm số trùng phương ( y= ax^4+bx^2+c )
- Điều kiện hàm trùng phương có 4 nghiệm
(left{begin{matrix} ab <0\ac>0 \b^2-4ac >0 end{matrix}right.)
- Điều kiện hàm trùng phương có 2 nghiệm
(left{begin{matrix} ac<0 \b^2-4ac geq 0 end{matrix}right.)
- Điều kiện hàm trùng phương vô nghiệm
(left[begin{array}{l}b^2-4ac <0 \ left{begin{matrix} b^2-4ac geq 0 \ ab >0 \ ac >0 end{matrix}right.end{array}right.)
Ví dụ:
Tìm số nghiệm của từng hàm số sau đây
a, ( y= x^4-5x^2+4 )
b, ( y= x^4 -x^2 -6 )
c , ( x^4 +3x^2 + 2 )
Cách giải:
a, Ta có
(left{begin{matrix} a=1\b=-5 \ c=4 end{matrix}right.Rightarrow left{begin{matrix} ab <0 \ac >0 \b^2-4ac = 9 >0 end{matrix}right.)
(Rightarrow) phương trình có ( 4 ) nghiệm
b, Ta có
(left{begin{matrix} a=1\b=-1 \ c=-6 end{matrix}right.Rightarrow left{begin{matrix} ac <0 \b^2-4ac = 25 >0 end{matrix}right.)
(Rightarrow) phương trình có ( 2 ) nghiệm
c, Ta có
(left{begin{matrix} a=1\b=3 \ c=2 end{matrix}right.Rightarrow left{begin{matrix} ab>0 \ ac >0 \b^2-4ac = 1 >0 end{matrix}right.)
(Rightarrow) phương trình vô nghiệm
Cực trị của hàm trùng phương
Hàm trùng phương có 3 cực trị khi nào?
Điều kiện hàm trùng phương có 3 cực trị:
Hàm số ( y= ax^4+bx^2+c ) có 3 cực trị (Leftrightarrow ab <0)
Khi đó:
Hàm số có 2 cực tiểu và 1 cực đại (Leftrightarrow left{begin{matrix} a>0\ b<0 end{matrix}right.)
Hàm số có 2 cực đại và 1 cực tiểu (Leftrightarrow left{begin{matrix} a<0\ b>0 end{matrix}right.)
Hàm trùng phương có 1 cực trị khi nào?
Điều kiện hàm trùng phương có 1 cực trị:
Hàm số ( y= ax^4+bx^2+c ) có 1 cực trị (Leftrightarrow ab geq 0)
Khi đó:
Hàm số có đúng 1 cực trị là cực tiểu ( Leftrightarrow left{begin{matrix} a>0\ bgeq 0 end{matrix}right.)
Hàm số có đúng 1 cực trị là cực đại ( Leftrightarrow left{begin{matrix} a<0\ bleq 0 end{matrix}right. )
Ví dụ:
Tìm m để hàm trùng phương không có cực đại
( mx^4 +2(m^2-4)m^2+m^2+1 )
Cách giải:
Để hàm số trùng phương không có cực đại thì hàm số chỉ có đúng một cực trị là cực tiểu
(Rightarrow left{begin{matrix} m>0 \ m^2-4 geq 0 end{matrix}right.)
(Leftrightarrow left{begin{matrix} m>0 \ left[begin{array}{l}mgeq 2\ m leq -2end{array}right. end{matrix}right.)
(Leftrightarrow m geq 2)
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết và bài tập về chuyên đề hàm số trùng phương cũng như các phương pháp giải. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề hàm trùng phương có 3 cực trị. Chúc bạn luôn học tốt!
Xem thêm >>> Cực trị của hàm số là gì?
Xem thêm >>> Công thức, Điều kiện và Bài tập cực trị của hàm số bậc 4