Phương trình hoành độ giao điểm là gì

Nội dung của chủ đề này đã được nhắc đến trong chương trình Toán lớp 9 bậc THCS. Ở kiến thức bậc THPT ý nghĩa của chủ đề phương trình hoành độ giao điểm lớp 12 ở mức phức tạp hơn vì hàm số đã đa dạng và có độ phức tạp hơn trước. Từ chiều biến thiên và ý nghĩa cực trị mà sự tương giao của đồ thị có thể biện luận một cách chặt chẽ và tường minh hơn.

1. Phương trình hoành độ giao điểm là gì?

Cho hai hàm số f(x) và g(x).

Xét phương trình hoành độ giao điểm f(x) = g(x).

Ta có:

• Số giao điểm của hai đồ thị = Số nghiệm của phương trình.

• Hoành độ giao điểm = Nghiệm của phương trình.

Hình vẽ minh họa:

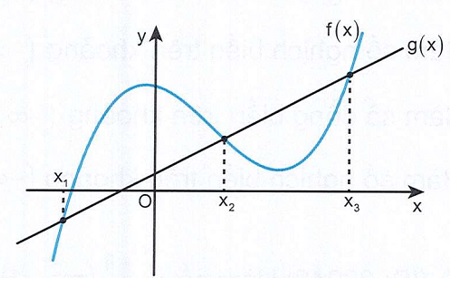
Đồ thị có ba giao điểm ⇔ phương trình f(x) = g(x) có ba nghiệm. Hoành độ giao điểm là nghiệm của f(x) = g(x).

2. Một số phép biến đổi đồ thị vận dụng giải quyết bài toán phương trình hoành độ giao điểm

2.1. Tịnh tiến đồ thị hàm số

Cho hàm số y = f(x) có đồ thị (C); p, q là 2 số dương tùy ý.

• Tịnh tiến (C) lên trên q đơn vị thì được đồ thị hàm số y = f(x) + q.

• Tịnh tiến (C) xuống dưới q đơn vị thì được đồ thị hàm số y = f(x) – q.

• Tịnh tiến (C) sang trái p đơn vị thì được đồ thị hàm số y = f(x + p).

• Tịnh tiến (C) sang phải p đơn vị thì được đồ thị hàm số y = f(x – p).

• Tịnh tiến (C) theo vectơ thì được đồ thị hàm số y = f(x + a) + b.

2.2. Đồ thị hàm số chứa dấu giá trị tuyệt đối

Từ đồ thị suy ra đồ thị

Ta có và là hàm chẵn

Nên đồ thị (C’) nhận Oy làm trục đối xứng.

Cách vẽ (C’) từ (C):

• Giữ nguyên phần đồ thị bên phải trục Oy của đồ thị (bỏ phần bên trái).

• Lấy đối xứng phần đồ thị bên phải trục Oy của đồ thị qua Oy.

Từ đồ thị suy ra đồ thị

Ta có

Cách vẽ (C’) từ (C):

• Giữ nguyên phần đồ thị bên trên trục Ox của đồ thị (bỏ phần bên dưới).

• Lấy đối xứng phần đồ thị bên dưới trục Ox của đồ thị qua Ox.

3. Xét phương trình hoành độ giao điểm giữa f(x) và g(x)

Tương giao đồ thị hàm số và trục Ox

• Cắt nhau tại ba điểm khi và chỉ khi Ð

• Cắt nhau tại hai điểm khi và chỉ khi Ð

• Cắt nhau tại một điểm khi và chỉ khi hoặc Ð

Tương giao đồ thị hàm số và đường thẳng (d):

Xét phương trình (1)

• Nhẩm nghiệm rồi đưa về phương trình bậc hai.

• Cô lập tham số sau đó khảo sát hàm số.

Tương giao đồ thị hàm số và trục Ox

• Cắt nhau tại bốn điểm khi và chỉ khi Ð

• Cắt nhau tại ba điểm khi và chỉ khi

Tương giao đồ thị hàm số và đường thẳng (d): .

Xét phương trình (2)

Đặt ta có phương trình (3)

• Cắt nhau tại bốn điểm ⇔ (2) có bốn nghiệm phân biệt.

⇔ (3) có hai nghiệm dương phân biệt.

⇔ (3) thỏa mãn .

• Cắt nhau tại ba điểm ⇔ (2) có ba nghiệm phân biệt.

⇔ (3) có hai nghiệm phân biệt, trong đó có một nghiệm dương và một nghiệm t = 0.

• Cắt nhau tại hai điểm ⇔ (2) có hai nghiệm phân biệt

⇔ (3) có nghiệm kép dương hoặc có hai nghiệm trái dấu.

• Cắt nhau tại một điểm ⇔ (2) có một nghiệm

⇔ (3) có hai nghiệm phân biệt, trong đó t = 0 và một nghiệm âm hoặc (3) có nghiệm kép t = 0.

• Không cắt nhau ⇔ (2) vô nghiệm

⇔ (3) vô nghiệm hoặc chỉ có nghiệm âm

Tương giao đồ thị hàm số và đường thẳng:

Xét phương trình ⇔ (4)

• Cắt nhau tại hai điểm ⇔ (4) có hai nghiệm phân biệt khác .

4. Bài tập phương trình hoành độ giao điểm không chứa tham số

Bài 1: Đồ thị hàm số cắt đồ thị hàm số tại hai điểm phân biệt A, B. Tính độ dài AB.

A. AB = 3

B. AB =

C. AB = 2

D. AB = 1

ĐÁP ÁN

∗ Phương pháp:

Viết phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm tọa độ giao điểm và tính khoảng cách.

Cho hai điểm

∗ Cách giải

Phương trình hoành độ giao điểm của (C) và (P) là

⇔ ⇔ ⇔

Khi đó → ⇒

→ Chọn câu D.

Bài 2: Cho hàm số y = f(x) có đồ thị là đường cong như hình vẽ bên. Tìm số nghiệm của phương trình

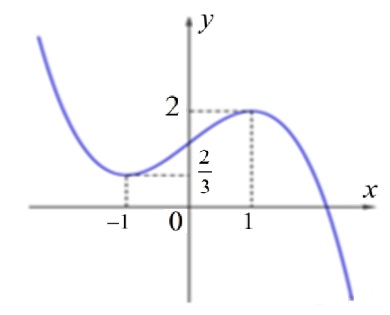
A. 3

B. 2

C. 1

D. 4

ĐÁP ÁN

∗ Phương pháp

Dựa vào phép suy đồ thị để xác định số giao điểm của hai đồ thị hàm số

∗ Cách giải

Hàm số y = f(x) có đồ thị (C), cắt đường thẳng y = 1 tại 3 điểm phân biệt.

Hàm số y = f(x+2018) có đồ thị (C1) là tịnh tiến đồ thị (C) sang trái 2018 đơn vị trên trục Ox.

Khi đó đồ thị (C1) cắt đường thẳng y = 1 tại 3 điểm phân biệt.

→ Chọn câu A.

Bài 3: Cho hàm số y = f(x) có bảng biến thiên như sau:

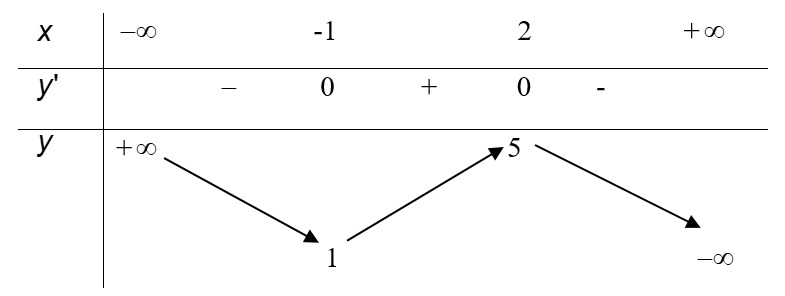
Số nghiệm của phương trình là

A. 0

B. 1

C. 3

D. 4

ĐÁP ÁN

∗ Cách giải

Từ bảng biến thiên y = f(x) suy ra bảng biến thiên của (giữ nguyên phần đồ thị nằm bên phải trục tung và

trên trục tung, lấy đối xứng phần đồ thị bên phải trục tung sang bên trái trục tung)

Quan sát bảng ta thấy: phương trình vô nghiệm.

→ Chọn câu A.

5. Bài tập phương trình hoành độ giao điểm chứa tham số

Bài 1: Cho hàm số có đồ thị (C). Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng

cắt (C) tại hai điểm phân biệt AB thỏa mãn

A.

B.

C.

D.

ĐÁP ÁN

∗ Phương pháp

Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có hai nghiệm phân biệt.

Tính độ dài đoạn thẳng AB, sử dụng định lí Vi-et.

∗ Cách giải

Xét phương trình hoành độ giao điểm:

⇔

⇔

Để (C) và d cắt nhau tại hai điểm phân biệt

⇔ Phương trình (*) có 2 nghiệm phân biệt khác -1.

⇔ ⇔ ⇔ ⇔

Khi đó gọi là hoành độ các điểm A, B là hai nghiệm của phương trình (*)

⇒ ⇒

Theo định lí Vi-et ta có:

⇒

⇒ ⇔ ⇔ ⇔

→ Chọn câu D.

Bài 2: Cho hàm số y = f(x) có bảng biến thiên như sau:

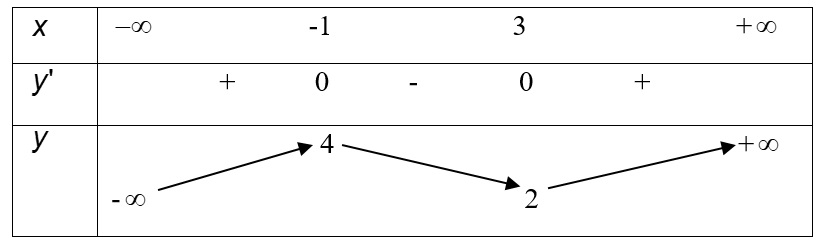
Tìm tất cả các giá trị thực của tham số m để phương trình có 3 nghiệm thực phân biệt?

A.

B.

C.