Đồng biến, nghịch biến là tính chất quan trọng được vận dụng nhiều trong khảo sát hàm số. Nhiều bạn học sinh đặt câu hỏi hàm số đồng biến khi nào? Phương pháp xét đồng biến, nghịch biến là gì? Qua bài viết này của GiaiNgo sẽ giúp các bạn ôn tập kiến thức để vận dụng vào bài tập. Cùng đón đọc nhé!
Khái niệm về sự đồng biến của hàm số
Cho K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là một hàm số xác định trên K.
Được tài trợ
Hàm số y = f(x) được gọi là đồng biến (tăng) trên K, nếu:
∀ x1, x2 ∊ K mà x1 < x2 thì f (x1) < f (x2) Biểu diễn đồ thị hàm số là một đường đi lên. Hàm số đồng biến hoặc nghịch biến trên K còn gọi chung là hàm số đơn điệu trên K.
Được tài trợ
Hàm số đồng biến khi nào?
Hàm số f đồng biến trên K khi và chỉ khi:
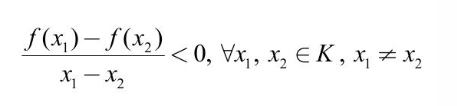
Điều kiện đủ để hàm số đồng biến
Cho hàm số f có đạo hàm trên K.
Nếu f'(x) > 0 với mọi x ∈ K thì hàm số f đồng biến trên K.
Phương pháp xét đồng biến và nghịch biến
Để xét tính đồng biến và nghịch biến của hàm số, ta cần áp dụng phương pháp sau:
- Tìm tập xác định
- Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,…, n) mà tại đó f'(x) bằng 0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ tìm m để hàm số đồng biến trên khoảng nghịch biến trên khoảng
Dạng 1: Tìm m để hàm số đồng biến trên R, nghịch biến trên R.
Dạng toán này thường gặp với đa thức bậc 3. Chúng ta có công thức như sau:

Ví dụ:
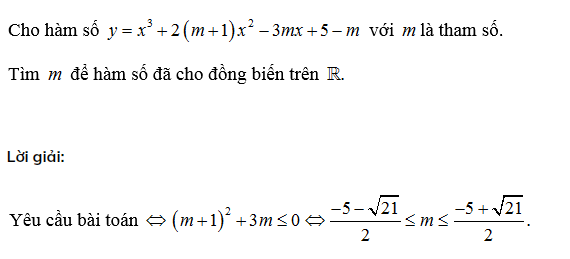
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến trên từng khoảng xác định
Dạng này ta thường gặp ở hàm phân tuyến tính (hay hàm số phân thức bậc 1 trên bậc 1). Ta áp dụng công thức sau:

Ví dụ:

Dạng 3: Nhẩm được nghiệm của đạo hàm
Ví dụ:
Cho hàm số y = x³ – (m+1)x² – (m²-2m)x + 2020. Tìm m để hàm số nghịch biến trên khoảng (0;1).
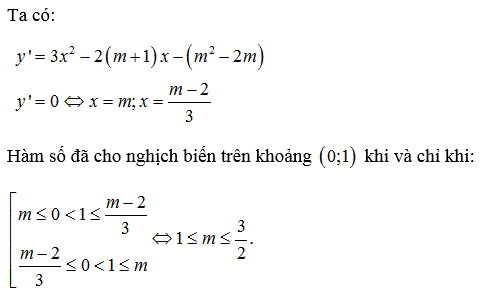
Dạng 4: Cô lập tham số m
Ví dụ:
Cho hàm số y = x³ + mx² + 2mx + 3. Tìm điều kiện của m để hàm số đồng biến trên khoảng (0;2).
Lời giải:
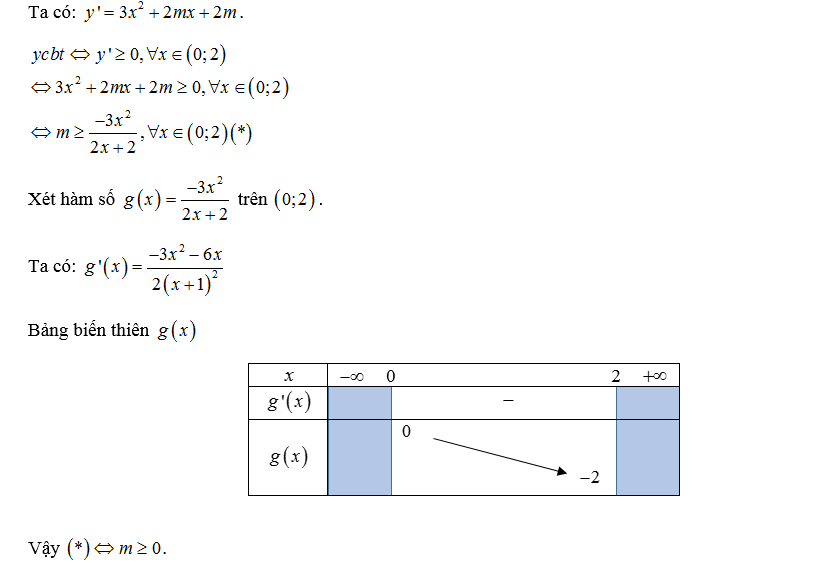
Dạng 5: Hàm phân tuyến tính đơn điệu trên khoảng cho trước
Nếu là hàm phân tuyến tính có tham số, trường hợp hàm số suy biến rất dễ xảy ra. Ta cần xét trường hợp hàm số suy biến thành hàm bậc nhất.
Trường hợp khác hàm suy biến thành hằng thì không cần xét vì hàm số này không phải hàm đơn điệu. Nếu xét hàm suy biến, có thể áp dụng công thức sau:

Ví dụ 1:
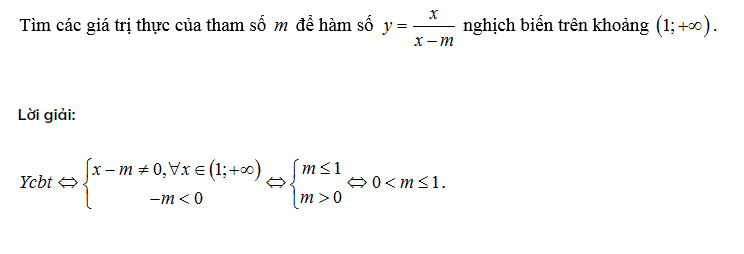
Ví dụ 2:
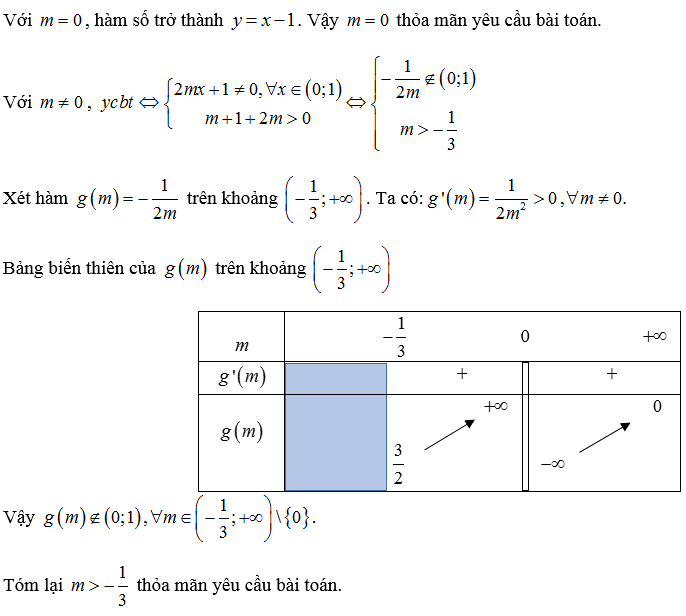
Trên đây là kiến thức về hàm số đồng biến khi nào, phương pháp giải và một số bài toán mẫu. Hy vọng có thể giúp bạn củng cố kiến thức và ôn tập tốt để làm tốt bài thi THPT quốc gia. Chúc các bạn thành công!