Bài viết khoảng cách giữa 2 đường thẳng bao gồm: công thức tính khoảng cách giữa 2 đường thẳng, khoảng cách giữa 2 đường thẳng chéo nhau, khoảng cách giữa 2 đường thẳng trong oxyz, khoảng cách giữa 2 đường thẳng trong không gian…

Khoảng cách giữa 2 đường thẳng trong mặt phẳng oxy

Cho 2 đường thẳng chéo nhau: d1 đi qua A có 1 VTCP d2 đi qua B có 1 VTCP

Khoảng cách từ điểm M đến đường thẳng d1

Tính khoảng cách giữa 2 đường thẳng d1 d2

Ví dụ:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng . Tính khoảng cách giữa d1 và d2.

Ta dễ dàng kiểm tra được d1 và d2 là hai đường thẳng song song, nên ta chỉ việc lấy một điểm bất kì thuộc d1, và tính khoảng cách từ điểm đó đến d2.

Gọi , .

Ta có:

Vậy:

Khoảng cách giữa 2 đường thẳng trong oxyz

Cách 1: đi qua M1. có 1 VTCP đi qua M2. có 1 VTCP

Cách 2: AB là đoạn vuông góc chung ,

Ví dụ:

Cho a) CMR: d1, d2 chéo nhau b) Tính d(d1;d2)

Lời giải: a) d1 đi qua M1(1;2;-3), có 1 VTCP d2 đi qua M2(2;-3;1), có 1 VTCP Vậy d1, d2 chéo nhau b)Cách 1:Cách 2: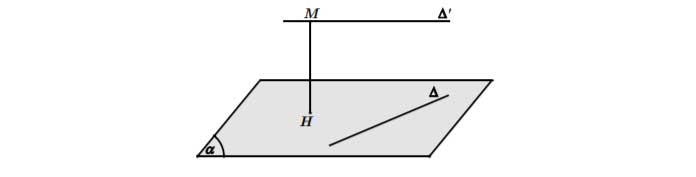 AB là đoạn vuông góc chung 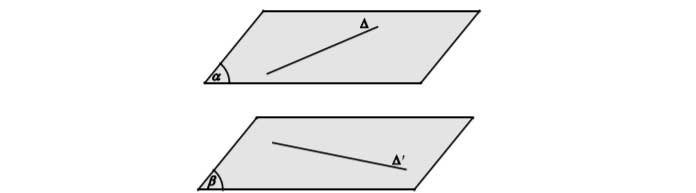AB = d(d1;d2)

Phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau

Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau: Dựng đoạn vuông góc chung MN của a và b. Khi đó . Sau đây là một số cách dựng đoạn vuông góc chung thường dùng :Phương pháp 1: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó

Phương pháp 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.

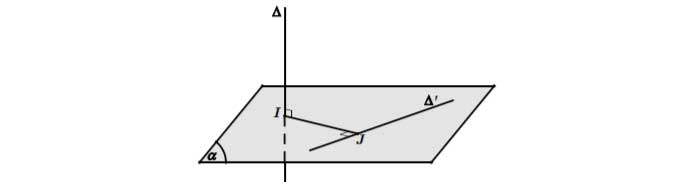
Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó. Trường hợp 1: ∆ và ∆’ vừa chéo nhau vừa vuông góc với nhau

• Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I.
• Bước 2: Trong mặt phẳng (α) kẻ .

Khi đó IJ là đoạn vuông góc chung và .

Trường hợp 2: ∆ và ∆’ chéo nhau mà không vuông góc với nhau

• Bước 1: Chọn mặt phẳng (α) chứa ∆’ và song song với ∆.
• Bước 2: Dựng d là hình chiếu vuông góc của ∆ xuống (α) bằng cách lấy điểm dựng đoạn 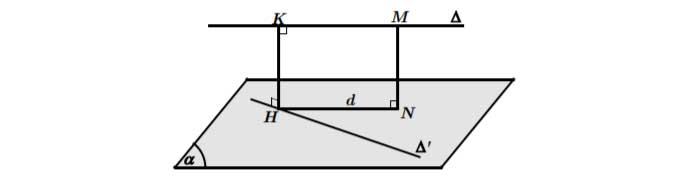, lúc đó d là đường thẳng đi qua N và song song với ∆.
• Bước 3: Gọi , dựng

Khi đó HK là đoạn vuông góc chung và .

Hoặc

• Bước 1: Chọn mặt phẳng 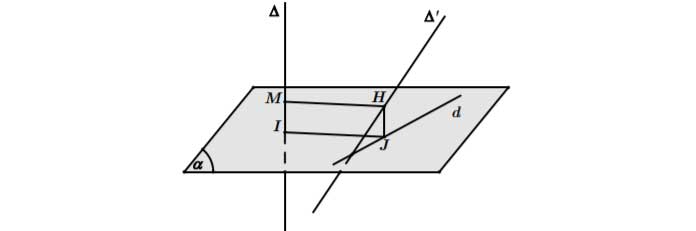tại I.
• Bước 2: Tìm hình chiếu d của ∆’ xuống mặt phẳng (α).
• Bước 3: Trong mặt phẳng (α), dựng , từ J dựng đường thẳng song song với ∆ cắt ∆’ tại H, từ H dựng .

Khi đó HM là đoạn vuông góc chung và .

Sử dụng phương pháp vec tơ a) MN là đoạn vuông góc chung của AB và CDkhi và chỉ khi b) Nếu trong (α) có hai vec tơ không cùng phương thì .Sotayhoctap chúc các bạn học tốt!