Nhắc đến sự đồng biến nghịch biến của hàm số lượng giác, chắc hẳn các em học sinh cấp 3 sẽ thấy dạng bài này rất thú vị và hay. Sau đây DINHNGHIA.VN sẽ chia sẻ một số kiến thức cơ bản về chủ đề này.
Sự đồng biến nghịch biến của hàm số là gì?
Giả sử: K là một khoảng, một đoạn hoặc một nửa khoảng.
Cho hàm số (y=f(x)) xác định trên K.
- Hàm số (y=f(x)) đồng biến trên K nếu: (x_{1},x_{2}in K; x_{1} < x_{2}Rightarrow f(x_{1})< f(x_{2}))
- Hàm số (y=f(x)) nghịch biến trên K nếu: (x_{1},x_{2}in K; x_{1} < x_{2}Rightarrow f(x_{1})> f(x_{2}))
Điều kiện cần và đủ để hàm số đồng biến, nghịch biến
Cho hàm số: (y=f(x)) có đạo hàm trên K.
- Điều kiện cần:
+ Nếu (f(x)) đồng biến trên K thì (f'(x)geq 0, forall xin K.)
+ Nếu (f(x)) nghịch biến trên K thì (f'(x)leq 0, forall xin K.)
- Điều kiện đủ:
+ Nếu (f'(x)geq 0, forall xin K) và (f'(x)=0) chỉ tại 1 số hữu hạn điểm thuộc K thì (f'(x)) đồng biến trên K.
+ Nếu (f'(x)leq 0, forall xin K) và (f'(x)=0) chỉ tại 1 số hữu hạn điểm thuộc K thì (f'(x)) nghịch biến trên K.
+ Nếu (f'(x)= 0, forall xin K) thì (f(x)) là hàm hằng trên K.
Các bước xét sự đồng biến, nghịch biến của hàm số
- Bước 1: Tìm tập xác định.
- Bước 2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3: Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Sự đồng biến nghịch biến của hàm số lượng giác
Hàm số lượng giác là hàm số có dạng y = sin x, y = cos x, y = tan x, y = cot x.
- Hàm số sin: Quy tắc đặt tương ứng với mỗi số thực x với số thực sin x.
(sin x: mathbb{R}rightarrow mathbb{R})
(xmapsto y=sin x)
được gọi là hàm số sin, ký hiệu là y = sin x.
Tập xác định của hàm số sin là: (mathbb{R})
- Hàm số cos: Quy tắc đặt tương ứng với mỗi số thực x với số thực cos x.
(cos x: mathbb{R}rightarrow mathbb{R})
(xmapsto y=cos x)
được gọi là hàm số cos, ký hiệu là y = cos x.
Tập xác định của hàm số sin là: (mathbb{R})
- Hàm số tan: là hàm số được xác định bởi công thức: (y=frac{sin x}{cos x} (cos x neq 0)), ký hiệu là y = tan x.
Tập xác định của hàm số tan là: (D=mathbb{R}setminus left { frac{pi }{2} +Kpi , kin mathbb{Z}right })
- Hàm số cot: là hàm số được xác định bởi công thức: (y=frac{cos x}{sin x} (sin x neq 0)), ký hiệu là y = cot x.
Tập xác định của hàm số y = cot x là: (D=mathbb{R}setminus left { kpi , kin mathbb{Z} right }).
Các dạng toán về tính đơn điệu của hàm số lượng giác
Khi tìm hiểu về sự đồng biến nghịch biến của hàm số lượng giác, các bạn cần nắm chắc các dạng toán như sau:
Dạng 1: Tìm tập xác định của hàm số lượng giác lớp 11
Ta có 4 hàm số lượng giác cơ bản như sau: y= sinx, y=cox, y =tanx và y = cotx. Mỗi hàm số trên đều có tập xác định riêng, cụ thể:
y = sinx , y = cosx có D = R.
y = tanx có D = R {π/2 +kπ, k ∈ Z}
y = cotx có tập xác định D = R { kπ, k ∈ Z}.
Phương pháp giải dạng bài tập này như sau:
Khi tìm hiểu về tính đơn điệu của hàm số lượng giác, bạn cần lưu ý một số kiến thức quan trọng như sau:
- Hàm số y = sinx sẽ đồng biến trên mỗi khoảng (-π/2 + k2π; π/2 +k2π), và nghịch biến trên mỗi khoảng (π/2 +k2π).
- Hàm số y = cosx sẽ nghịch biến trên mỗi khoảng (k2π; π + k2π), và đồng biến trên khoảng (-π +k2π; k2π).
- Hàm số y = tanx sẽ đồng biến trên mỗi khoảng (-π/2 +kπ; π/2 +kπ).
- Hàm số y = cotx sẽ nghịch biến trên mỗi khoảng (kπ; π +kπ).
Dạng 2: Tìm tính đơn điệu của hàm số lượng giác
Với dạng toán về tính đơn điệu của hàm số lượng giác, bạn hoàn toàn có thể sử dụng máy tính cầm tay để giải nhanh dạng toán này, cụ thể:
Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Để tìm giá trị lớn nhất của hàm số hay giá trị nhỏ nhất của hàm số, bạn cần ghi nhớ lý thuyết sau:
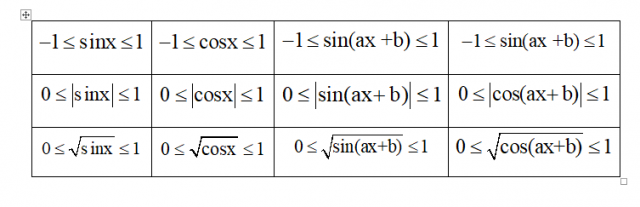
Dạng 4: Tính chẵn lẻ của hàm số lượng giác
Phương pháp giải bài tập về tính chẵn lẻ của hàm số lượng giác như sau:
- Hàm số y = f(x) với tập xác định D gọi làm hàm số chẵn nếu:
- Với ∀ x ∈ D thì -x ∈ D và f(x) = f(-x). Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
- Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu:
- Với ∀ x ∈ D thì -x ∈ D và f(-x) = -f(x).
- Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.
Dạng 5: Tính tuần hoàn của hàm số lượng giác
Với dạng toán về tính tuần hoàn của hàm số lượng giác, bạn cần làm theo các bước như sau:
- Hàm số y = f(x) xác định trên tập D được gọi là hàm số tuần hoàn nếu có số T ≠ 0, sao cho ∀ x ∈ D. Khi đó x ± T∈ D và f(x+T) = f(x).
- ***Lưu ý: Các hàm số y = sin (ax +b), y = cos (ax+b) tuần hoàn với chú kì T = 2π/|a|
- Các hàm số tan (ax +b), y = cot(ax+ b) tuần hoàn với chu kì T = π/|a|.
Sự đồng biến nghịch biến của hàm số mũ và hàm số logarit
Định nghĩa sự đồng biến nghịch biến của hàm số mũ và hàm số logarit
- Hàm số mũ là hàm số có dạng y= ax (với a > 0, a≠1).
- Hàm số logarit là hàm số có dạng y = logax (với a > 0, a≠1)
Tính chất của hàm số mũ y= ax (a > 0, a≠1).
- Tập xác định: (mathbb{R})
- Đạo hàm: (forall xin mathbb{R}, y= a^{x}lna)
- Chiều biến thiên:
- Nếu a>1 thì hàm số luôn đồng biến.
- Nếu 0<a<1 thì hàm số luôn nghịch biến.
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành (y= ax > 0, ∀x), và luôn cắt trục tung tại điểm (0;1) và đi qua điểm (1;a).
Tính chất của hàm số logarit y = logax (a> 0, a≠1).
- Tập xác định: ((0;+infty ))
- Đạo hàm: (forall x in (0;+infty ), y=frac{1}{xlna})
- Chiều biến thiên:
- +) Nếu a>1 thì hàm số luôn đồng biến.
- +) Nếu 0 < a < 1 thì hàm số luôn nghịch biến.
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
Lưu ý:
- Nếu a > 1 thì (lna>0), suy ra ((a^{x})’>0, forall x) và ((log_{a}x)’>0, forall x> 0); Hàm số mũ và hàm số logarit với cơ số lớn hơn 1 là những hàm số luôn đồng biến.
- Nếu 0 < a < 1 thì (lna<0), ((a^{x})'< 0) và ((log_{a}x)’< 0, forall x> 0); hàm số mũ và hàm số logarit với cơ số nhỏ hơn 1 là những hàm số luôn nghịch biến.
– Công thức đạo hàm của hàm số logarit có thể mở rộng thành:
((lnleft| x right|)’=frac{1}{x}, forall xneq 0) và ((log_{a}left| x right|)’= frac{1}{xlna}, forall x≠0).
Ví dụ sự đồng biến nghịch biến của hàm số lượng giác
Tìm các khoảng đồng biến của hàm số: (y= x^{2}e^{-4x})
Tập xác định: (mathbb{R})
Ta có: (y’= 2xe^{-4x}+xe^{-4x}(-4)=2xe^{-4x}(1-2x))
Khoảng đồng biến của hàm số là (1; +∞).
Như vậy, bài viết trên đã cung cấp cho bạn những kiến thức bổ ích về sự đồng biến nghịch biến của hàm số, sự đồng biến nghịch biến của hàm số lượng giác cũng như các ví dụ minh họa. Nếu như có bất cứ băn khoăn hay câu hỏi nào về sự đồng biến và nghịch biến của hàm số lượng giác, mời bạn để lại nhận xét bên dưới để chúng mình cùng trao đổi thêm nhé!
Xem thêm:
- Giới hạn của hàm số là gì? Lý thuyết, Bài tập và Cách giải
- Giới hạn của dãy số lớp 11: Lý thuyết, Bài tập và Các dạng toán
- Chuyên đề các phép biến hình: Lý thuyết và Các dạng bài tập
Tu khoa lien quan:
- hàm số lượng giác 11 cơ bản
- xét tính đơn điệu của hàm số lượng giác
- cách vẽ đồ thị hàm số lượng giác lớp 11
- tính đơn điệu của hàm số lượng giác lớp 11
- sự đồng biến nghịch biến của hàm số lượng giác
- xét tính đồng biến nghịch biến của hàm số y=sinx
- tìm m để hàm số lượng giác đồng biến trên khoảng
- bài tập đồng biến nghịch biến của hàm số lượng giác 12
- xét tính đồng biến nghịch biến của hàm số lượng giác bằng máy tính
Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!