Mặt cầu ngoại tiếp hình chóp – Cách giải nhanh chính xác 100%

Trong bài viết dưới đây, chúng tôi chia sẻ kiến thức về mặt cầu ngoại tiếp hình chóp thường kết hợp giữa khối đa diện và khối cầu bằng phương pháp xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp kèm theo ví dụ có lời giải chi tiết để các bạn cùng tham khảo nhé

Cách xác tâm và bán kính mặt cầu ngoại tiếp hình chóp

Phương pháp

Xác định trục d của đường tròn ngoại tiếp đa giác đáy ( d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).

Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục Δ của đường tròn ngoại tiếp một đa giác của mặt bên).

Giao điểm I của (P) và d (hoặc Δ của và d) là tâm mặt cầu ngoại tiếp hình chóp.

Bán kính của mặt cầu ngoại tiếp hình chóp là độ dài đoạn thẳng nối tâm I với một đỉnh của hình chóp.

Lưu ý: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.

Tham khảo thêm:

• Diện tích mặt cầu và các dạng bài tập có lời giải chi tiết từ A – Z
• Phương trình mặt cầu và các dạng bài tập đầy đủ
• Công thức tính thể tích khối cầu

Các dạng hình chóp thường gặp và cách xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.

Dạng 1. Hình chóp có các điểm cùng nhìn một đoạn thẳng AB dưới một góc vuông

Phương pháp:

• Tâm: Trung điểm của đoạn thẳng AB
• Bán kính: R =AB/2

Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt phẳng (ABC) và SC = 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

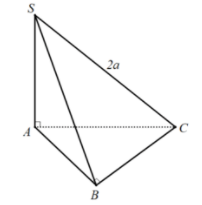
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB

SA ⊥ (ABC) ⇒ SA ⊥ BC

Suy ra hai điểm A, B cùng nhìn SC dưới một góc vuông.

Vậy bán kính mặt cầu ngoại tiếp hình chóp S.ABC là: R = SC/2 = 2a/2 = a

Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tại A, SA vuông góc với mặt phẳng (ABCD) và SC = 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.

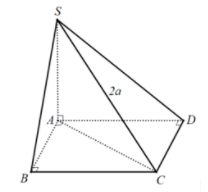
Chứng minh tương tự ta được: CD ⊥ SD

SA ⊥ (ABCD) ⇒ SA ⊥ AC

Ba điểm A, B, D cùng nhìn SC dưới một góc vuông.

Vậy bán kính mặt cầu là R = SC/2 = 2a/2 = a

Dạng 2: Hình chóp đều.

Phương pháp: Khối chóp đều có cạnh bên SA và chiều cao SO thì bán kính mặt cầu ngoại tiếp khối chóp là

R = SA2/2SO

Chứng minh:

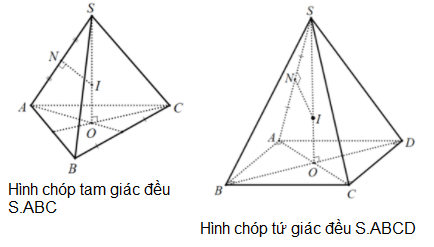
Gọi O là tâm của đáy ⇒ SO là trục của đường tròn ngoại tiếp đa giác đáy.

Trong mặt phẳng xác định bởi SO và một cạnh bên, chẳng hạn như (SAO), ta vẽ đường trung trực của cạnh SA và cắt SO tại I ⇒ I là tâm của mặt cầu ngoại tiếp hình chóp.

Ta có: ΔSNI ∼ ΔSOA ⇒ SN/SO = SI/SA, suy ra bán kính mặt cầu ngoại tiếp hình chóp là:

Ví dụ 1: Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.

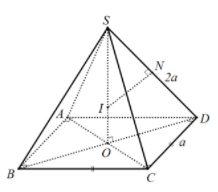
Gọi O là tâm đáy thì SO là trục của hình vuông ABCD. Gọi N là trung điểm của SD, trong (SDO) kẻ trung trực của đoạn SD cắt SO tại I thì IS = IA = IB = IC = ID nên I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD . Bán kính mặt cầu là R = SI.

Ta có: ΔSNI ∼ ΔSOA ⇒ SN/SO = SI/SD ⇒ R = SI = SD. SN / SO = SD2/SO

Dạng 3. Hình chóp có cạnh bên vuông góc với mặt phẳng đáy.

Phương pháp: Cho hình chóp S.A1A2…An có cạnh bên SA ⊥ (A1A2…An) và đáy A1A2…An nội tiếp được trong đường tròn tâm O. Tâm và bán kính mặt cầu ngoại tiếp hình chóp S.A1A2…An được xác định như sau:

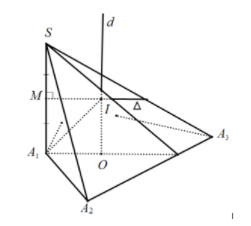
Từ tâm O ngoại tiếp của đường tròn đáy, ta vẽ đường thẳng d vuông góc với (A1A2…An) tại O.

Trong (d, SA1), ta dựng đường trung trực Δ của cạnh SA ,cắt SA1 tại N, cắt d tại I .

Khi đó: I là tâm mặt cầu ngoại tiếp hình chóp, bán kính R = IA1 = IA2 =… = IAn = IS . Tìm bán kính: Ta có: MIOA1 là hình chữ nhật, xét MA1I vuông tại M có:

Ví dụ: Cho hình chóp S.ABC có cạnh SA vuông góc với đáy, ABC là tam giác cân tại A và AB = a, góc BAC = 1200, SA = 2a. Tính bán kính của mặt cầu ngoại tiếp hình chóp S.ABC

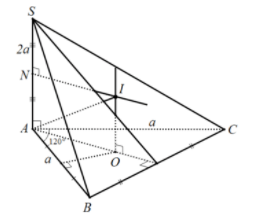
Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC.

Dựng trục d của đường tròn ngoại tiếp tam giác ABC; trong mặt phẳng (SA,d) vẽ trung trực cạnh SA và cắt d tại I.

Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC và bán kính R = IA = IB = IC = IS

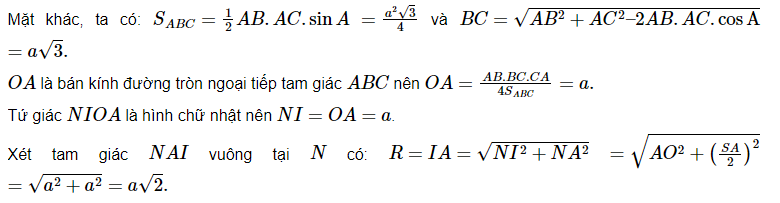
Dạng 4. Hình chóp có mặt bên vuông góc với mặt phẳng đáy.

Giả sử hình chóp có mặt bên SAB là tam giác đều, cân tại S, vuông tại S và đồng thời nằm trong mặt phẳng vuông góc với đáy. Gọi Rd là bán kính đường tròn ngoại tiếp tam giác SAB. Gọi Rd là bán kính đường tròn ngoại tiếp đáy. Bán kính khối cầu ngoại tiếp hình chóp đó là

Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Tổng hợp công thức tính mặt cầu ngoại tiếp hình chóp

Sau khi đọc xong bài viết của chúng tôi các bạn có thể nắm được các phương pháp xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp để áp dụng vào làm bài tập chính xác nhé