Viết phương trình đường thẳng đi qua hai điểm có VD từ A – Z

Theo khảo sát gần đây của chúng tôi cho thấy có rất nhiều các bạn học sinh không biết cách viết phương trình đường thẳng đi qua hai điểm như thế nào? Chính vì vậy, chúng tôi sẽ chia sẻ cách viết phương trình đường thẳng đi qua hai điểm cực trị, thuộc trục tọa độ,..để các bạn cùng tham khảo nhé

Cách viết phương trình đường thẳng đi qua hai điểm

Trong mặt phẳng Oxy cho hai điểm A(xa, ya), B(xb, yb). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

1. Sử dụng định nghĩa

• Bước 1: Tính vecto AB→ = (xb− xa;yb − ya) (vectơ chỉ phương của đường thẳng d)
• Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: n→ = (ya − yb; xb− xa)
• Bước 3: Viết phương trình đường thẳng d: (ya – yb)(x – xa) + (xb – xa)(y – ya) = 0

2. Sử dụng phương trình tổng quát

Bước 1: Gọi phương trình đường thẳng AB là : y = ax+b Bước 2: Lần lượt thay vào tọa độ A;B ta được:

Bước 3: Giải hệ phương trình trên tìm được a;b. Thay vào ta được phương trình đường thẳng AB

Lưu ý: Cách này chỉ áp dụng với những phương trình đường thẳng dạng ax + by + c = 0 với a,b≠0

Ví dụ 1: Trong mặt phẳng Oxy cho hai điểm A(2;4) và B(4;−1). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm A;B

Lời giải:

Ta có :

AB→ = (2;−5)

n→ = (5;2) là vectơ pháp tuyến của đường thẳng AB

Vậy phương trình đường thẳng AB là :

5(x−2)+2(y−4)=0

⇔ 5x + 2y − 18 =0

Ví dụ 2: Viết phương trình đường thẳng y = ax + b biết

a) Đi qua 2 điểm A(-3,2), B (5,-4). Tính diện tích tam giác được tạo bởi đường thẳng và 2 trục tọa độ.

b) Đi qua A (3,1) song song với đường thẳng y = -2x + m -1

Lơi giải:

a. Gọi phương trình tổng quát là: y = ax + b

Do PTĐT đi qua 2 điểm A, B nên ta có:

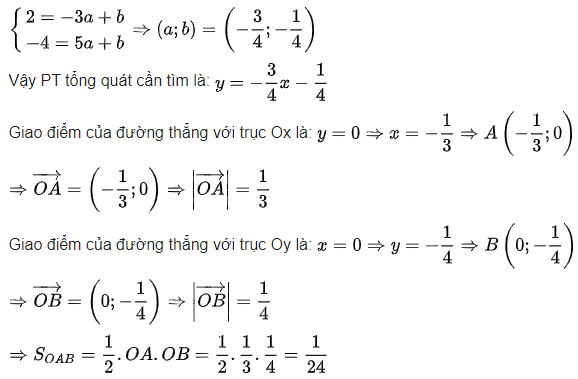
b. Gọi phương trình tổng quát là: y = ax + b

Do đường thẳng song song với y = -2x + m -1 ⇒ a = -2

Phương trình đường thẳng trở thành y = -2x + b

Mà đường thẳng qua điểm A(3; 1)

⇒ 1 = 3.(-2) + b ⇒ b = 7

Vậy phương trình tổng quát là: y = -2x + 7

Tham khảo:

• Các dạng phương trình đường thẳng
• Các dạng viết phương trình tiếp tuyến của đồ thị hàm số
• Phương trình lượng giác cơ bản

Phương trình đường thẳng đi qua 2 điểm thuộc trục tọa độ

Trong mặt phẳng tọa độ, cho điểm A(xa, ya), B(xb, yb) phân biệt.

Nếu hoành độ của A và B khác nhau, đồng thời tung độ của A và B khác nhau. Thì ta có thể dùng công thức sau để viết nhanh phương trình đường thẳng AB:

Nếu hoành độ điểm A và B giống nhau thì phương trình đường thẳng AB là: x = xa. Đường thẳng khi này song song hoặc trùng với trục Oy.

Nếu tung độ điểm A và B giống nhau thì phương trình đường thẳng AB là: y = ya.Đường thẳng khi này song song hoặc trùng với trục Ox.

Nếu A(a;0) và B(0;b) trong đó a.b≠0 thì phương trình AB được viết theo công thức:

Ví dụ: Trong mặt phẳng Oxy cho hai điểm A(0;1) và B(2;0). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm A;B

Cách giải:

Vì hai điểm A;B nằm trên hai trục tọa độ nên ta sử dụng phương trình đường thẳng theo đoạn chắn :

AB: x/3 + y = 0 ⇔ x + 3y = – 3

Phương trình đường thẳng đi qua hai điểm cực trị

Xét hàm số y = ax3 + bx2 + cx + d (a ≠ 0)

Hàm số có cực trị khi và chỉ khi phương trình y’ = 0 có hai nghiệm phân biệt x1; x2

Thực hiện phép chia f(x) cho f'(x) ta được f(x) = Q(x).f'(x) + ax + b

Gọi (x1;y1) và (x2;y2) là các điểm cực trị thì f'(x1) = f'(x2) = 0

Suy ra phương trình đường thẳng đi qua 2 điểm cực trị là y = ax + b.

Ví dụ: Biết đồ thị hàm số y = x3 – 3mx2 + 3(m2 – 1)x – m3 có hai điểm cực trị A và B. Viết phương trình đường thẳng AB.

Lời giải

Thực hiện phép chia y cho y’ ta được phương trình đường thẳng đi qua hai điểm cực trị A và B là

AB: y = (-m2 + 6m – 9)x – m2 + 3m – 3

Ví dụ 3: Tìm m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2×3 + 3(m – 1)x2 + 6(m – 2)x – 1 song song với đường thẳng y = -4x + 1.

Lời giải

Ta có y’ = 6×2 + 6(m – 1)x + 6(m – 2)

Hàm số có cực trị ⇔ y’ = 0 có 2 nghiệm phân biệt

⇔ Δ’ > 0 ⇔ 9(m – 1)2 – 36(m – 2) > 0 ⇔ 9(m – 3)2 > 0 ⇔ m ≠ 3

Thực hiện phép chia y cho y’ ta có phương trình đường thẳng đi qua 2 điểm cực trị là:

d: y = (-m2 + 6m – 9)x – m2 + 3m – 3

Khi đó d song song với đường thẳng y = -4x + 1

Kết hợp điều kiện ta có m = 1 hoặc m = 5

Hy vọng với những kiến thức mà chúng tôi vừa chia sẻ phía trên có thể giúp bạn nắm được các dạng viết phương trình đường thẳng đi qua 2 điểm để áp dụng vào làm bài tập nhé