Hướng dẫn sử dụng máy tính casio tìm số nghiệm phương trình logarit – Công thức nguyên hàm

1) PHƯƠNG PHÁP SỬ DỤNG MODE 7 Tổng hợp phương pháp Bước 1: Chuyển PT về dạng Vế trái = 0 Bước 2: Sử dụng chức năng MODE 7 để xét lập bảng giá trị của vế trái Bước 3: Quan sát và đánh giá : +) Nếu $Fleft( alpha right) = 0$ thì $alpha $ là 1 nghiệm +) Nếu $Fleft( a right).Fleft( b right) < 0$ thì PT có 1 nghiệm thuộc $left( {a;b} right)$

2) VÍ DỤ MINH HỌA VD1-[THPT Phạm Hồng Thái – Hà Nội 2017] Số nghiệm của phương trình ${6.4^x} – {12.6^x} + {6.9^x} = 0$ là ; A. 3 B. 1 C. 2 D. 0

GIẢI Khởi động chức năng lập bảng giá trị MODE 7 của Casio rồi nhập hàm Ta thấy khi x=0 thì F(0)=0 vậy x=0 là nghiệm.  Tiếp tục quan sát bảng giá trị F(X)  nhưng không có giá trị nào làm cho F(X)=0 hoặc khoảng nào làm cho F(X) đổi dấu. Điều này có nghĩa x=0 là nghiệm duy nhất Kết luận : Phương trình ban đầu có 1 nghiệm $ Rightarrow $ Ta chọn đáp án B Cách tham khảo : Tự luận Vì ${9^x} > 0$ nên ta có thể chia cả 2 vế cho ${9^x}$ Phương trình đã cho $ Leftrightarrow 6.frac{{{4^x}}}{{{9^x}}} – 12.frac{{{6^x}}}{{{9^x}}} + 6 = 0$ $ Leftrightarrow 6.{left( {frac{2}{3}} right)^{2x}} – 12.{left( {frac{2}{3}} right)^x} + 6 = 0$ (1) Đặt ${left( {frac{2}{3}} right)^x}$ là t thì ${left( {frac{2}{3}} right)^{2x}} = {t^2}$ . Khi đó (1) $ Leftrightarrow 6{t^2} – 12t + 6 = 0 Leftrightarrow 6{left( {t – 1} right)^2} = 0 Leftrightarrow t = 1$ Vậy ${left( {frac{2}{3}} right)^x} = 1 Leftrightarrow x = 0$ Bình luận : Để sử dụng phương pháp Casio mà không bị sót nghiệm ta có thể sử dụng vài thiết lập miền giá trị của X để kiểm tra. Ngoài Start -9 End 10 Step 1 ta có thể thiết lập Start -4 End 5 Start 0.5 Ta quan sát bảng giá trị vẫn có 1 nghiệm x=0 duy nhất vậy ta có thể yên tâm hơn về lựa chọn của mình. Theo cách tự luận ta thấy các số hạng đều có dạng bậc 2. Ví dụ ${4^x} = {left( {{2^x}} right)^2}$ hoặc ${6^x} = {2^x}{.3^x}$ vậy ta biết đây là phương trình dạng đẳng cấp bậc 2. Dạng phương trình đẳng cấp bậc 2 là phương trình có dạng $m{a^2} + nab + p{b^2} = 0$ ta giaỉ bằng cách chia cho ${b^2}$ rồi đặt ẩn phụ là $frac{a}{b} = t$

VD2-[Thi thử chuyên Thái Bình lần 1 năm 2017] Số nghiệm của phương trình ${e^{sin left( {x – frac{pi }{4}} right)}} = tan x$ trên đoạn $left[ {0;2pi } right]$ là : A. 1 B. 2 C. 3 D. 4 GIẢI Chuyển phương trình về dạng : ${e^{sin left( {x – frac{pi }{4}} right)}} – tan x = 0$ Sử dụng chức năng MODE 7 với thiết lập Start 0 End $2pi $ Step $frac{{2pi – 0}}{{19}}$ 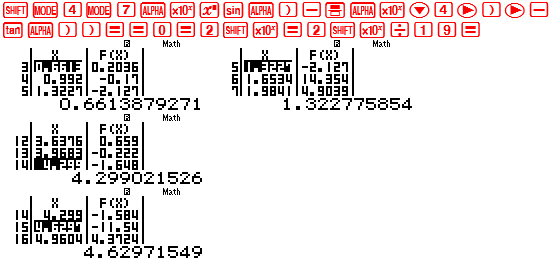Quan sát bảng giá trị ta thấy 3 khoảng đổi dấu như trên : $fleft( {0.6613} right).fleft( {0.992} right) < 0$ $ Rightarrow $ có nghiệm thuộc khoảng $left( {0.6613;0.992} right)$ $fleft( {1.3227} right).fleft( {1.6634} right) < 0$ $ Rightarrow $ có nghiệm thuộc khoảng $left( {1.3227;1.6534} right)$ $fleft( {3.6376} right).fleft( {3.9683} right) < 0$ $ Rightarrow $ có nghiệm thuộc khoảng $left( {3.6376;3.9683} right)$ $fleft( {4.6297} right).fleft( {4.9604} right) < 0$ $ Rightarrow $ có nghiệm thuộc khoảng $left( {4.6297;4.9604} right)$ Kết luận : Phương trình ban đầu có 4 nghiệm $ Rightarrow $ Ta chọn đáp án D Bình luận : Đề bài yêu cầu tìm nghiệm thuộc $left[ {0;2pi } right]$ nên Start = 0 và End = $2pi $ Máy tính Casio tính được bảng giá trị gồm 19 giá trị nên bước nhảy Step = $frac{{2pi – 0}}{{19}}$

VD3-[THPT Nhân Chính – Hà Nội 2017] Phương trình ${left( {sqrt 3 + sqrt 2 } right)^{frac{{3x}}{{x – 1}}}} = {left( {sqrt 3 – sqrt 2 } right)^x}$ có số nghiệm âm là : A. 2 nghiệm B. 3 nghiệm C. 1 nghiệm D. Không có GIẢI chuyển phương trình về dạng : ${left( {sqrt 3 + sqrt 2 } right)^{frac{{3x}}{{x – 1}}}} – {left( {sqrt 3 – sqrt 2 } right)^x} = 0$ Khởi động chức năng lập bảng giá trị MODE 7 của Casio rồi nhập hàm : Vì đề bài yêu cầu nghiệm âm nên ta hiết lập miền giá trị của X là : Start -9 End 0 Step 0.5 Máy tính cho ta bảng giá trị : Ta thấy khi x=-4 thì F (-4) =0 vậy x= -4 là nghiệm. Tiếp tục quan sát bảng giá trị F(X) nhưng không có giá trị nào làm cho F(X)=0 hoặc khoảng nào làm cho F(X) đổi dấu. Điều này có nghĩa x= -4 là nghiệm âm duy nhất Kết luận : Phương trình ban đầu có 1 nghiệm âm $ Rightarrow $ Ta chọn đáp án C Cách tham khảo : Tự luận Logarit hai vế theo cơ số dương $sqrt 3 + sqrt 2 $ Phương trình ${left( {sqrt 3 + sqrt 2 } right)^{frac{{3x}}{{x – 1}}}} = {left( {sqrt 3 – sqrt 2 } right)^x}$ $ Leftrightarrow {log _{sqrt 3 + sqrt 2 }}{left( {sqrt 3 + sqrt 2 } right)^{frac{{3x}}{{x – 1}}}} = {log _{sqrt 3 + sqrt 2 }}{left( {sqrt 3 – sqrt 2 } right)^x}$ $ Leftrightarrow frac{{3x}}{{x + 1}} = x{log _{sqrt 3 + sqrt 2 }}left( {sqrt 3 – sqrt 2 } right)$ $ Leftrightarrow frac{{3x}}{{x + 1}} = – x Leftrightarrow xleft( {frac{3}{{x + 1}} + 1} right) = 0 Leftrightarrow left[ begin{array}{l} x = 0\ x + 1 = – 3 Leftrightarrow x = – 4 end{array} right.$ x= -4 thỏa điều kiện. Vậy ta có x= -4 là nghiệm âm thỏa phương trình Bình luận : •Phương trình trên có 2 cơ số khác nhau và số mũ có nhân tử chung. Vậy đây là dấu hiệu của phương pháp Logarit hóa 2 vế •Thực ra phương trình có 2 nghiệm $x = 0;x = – 4$ nhưng đề bài chỉ hỏi nghiệm âm nên ta chỉ chọn nghiệm x=-4 và chọn đáp án C là đáp án chính xác •Vì đề bài hỏi nghiệm âm nên ta thiết lập miền giá trị của x cũng thuộc miền âm (-9;0)

VD4-[THPT Yến Thế – Bắc Giang 2017] Số nghiệm của phương trình ${left( {3 – sqrt 5 } right)^x} + 7{left( {3 + sqrt 5 } right)^x} = {2^{x + 3}}$ là : A. 2 B. 0 C. 3 D. 1 GIẢI Chuyển phương trình về dạng : ${left( {3 – sqrt 5 } right)^x} + 7{left( {3 + sqrt 5 } right)^x} – {2^{x + 3}} = 0$ Khởi động chức năng lập bảng giá trị MODE 7 của Casio rồi nhập hàm: Thiết lập miền giá trị của X là : Start -9 End 10 Step 1 Máy tính cho ta bảng giá trị: Ta thấy khi x=0 thì F(0)=0 vậy x=0 là nghiệm. Tiếp tục quan sát bảng giá trị F(X) Ta lại thấy $fleft( { – 3} right).fleft( { – 2} right) < 0$ vậy giữa khoảng $left( { – 3; – 2} right)$ tồn tại 1 nghiệm Kết luận : Phương trình ban đầu có 2 nghiệm $ Rightarrow $ Ta chọn đáp án A Cách tham khảo : Tự luận Vì ${2^x} > 0$ nên ta có thể chia cả 2 vế cho ${2^x}$ Phương trình đã cho $ Leftrightarrow {left( {frac{{3 – sqrt 5 }}{2}} right)^x} + 7{left( {frac{{3 + sqrt 5 }}{2}} right)^x} – 8 = 0$ Đặt ${left( {frac{{3 – sqrt 5 }}{2}} right)^x} = t$ $left( {t > 0} right)$ thì ${left( {frac{{3 + sqrt 5 }}{2}} right)^x} = frac{1}{t}$ . Khi đó (1) $ Leftrightarrow t + 7.frac{1}{t} – 8 = 0 Leftrightarrow {t^2} – 8t + 7 = 0 Leftrightarrow left[ begin{array}{l} t = 1\ t = 7 end{array} right.$ Với $t = 1 Leftrightarrow {left( {frac{{3 – sqrt 5 }}{2}} right)^x} = 1 Leftrightarrow x = 0$ Với $t = 7 Leftrightarrow {left( {frac{{3 – sqrt 5 }}{2}} right)^x} = 7 Leftrightarrow x = {log _{frac{{3 – sqrt 5 }}{2}}}7$ Vậy phương trình ban đầu có 2 nghiệm $x = 0;x = {log _{frac{{3 – sqrt 5 }}{2}}}7$ Bình luận : • Nhắc lại một lần nữa nếu $fleft( a right).fleft( b right) < 0$ thì phương trình có nghiệm thuộc $left( {a;b} right)$ • Ta nhận thấy 2 đại lượng nghịch đảo quen thuộc $frac{{3 + sqrt 5 }}{2}$ và $frac{{3 – sqrt 5 }}{2}$ nên ta tìm cách để tạo ra 2 đại lượng này bằng cách chia cả 2 vế của phương trình cho ${2^x}$

VD5: Số nghiệm của bất phương trình ${left( {2 + sqrt 3 } right)^{{x^2} – 2x + 1}} + {left( {2 – sqrt 3 } right)^{{x^2} – 2x – 1}} = frac{4}{{2 – sqrt 3 }}$ (1) là : A. 0 B. 2 C. 3 D. 5 GIẢI Chuyển bất phương trình (1) về dạng : ${left( {2 + sqrt 3 } right)^{{x^2} – 2x + 1}} + {left( {2 – sqrt 3 } right)^{{x^2} – 2x – 1}} – frac{4}{{2 – sqrt 3 }} = 0$ Nhập vế trái vào máy tính Casio : $Fleft( X right) = {left( {2 + sqrt 3 } right)^{{x^2} – 2x + 1}} + {left( {2 – sqrt 3 } right)^{{x^2} – 2x – 1}} – frac{4}{{2 – sqrt 3 }}$ (2+s3$)^Q)dp2Q)+1$+(2ps3$)^Q)dp2Q)p1$pa4R2ps3$$ Thiết lập miền giá trị cho x với Start -9 End 9 Step 1 Máy tính Casio cho ta bảng giá trị: Ta thấy $fleft( { – 1} right).fleft( 0 right) < 0$ vậy phương trình có 1 nghiệm thuộc (-1,0) Ta thấy f(1)=0 vậy x=1 là nghiệm của phương trình (1) Lại thấy $fleft( 2 right).fleft( 3 right) < 0$ vậy phương trình có 1 nghiệm thuộc (2;3) Kết luận : Phương trình (1) có 3 nghiệm $ Rightarrow $ Chọn đáp án C

BÀI TẬP TỰ LUYỆN

Bài 1-[Chuyên Khoa Học Tự Nhiên 2017] Số nghiệm của phương trình $log {left( {x – 1} right)^2} = sqrt 2 $ là : A. 2 B. 1 C. 0 D. Một số khác Bài 2-[THPT Lục Ngạn – Bắc Giang 2017] Số nghiệm của phương trình $left( {x – 2} right)left[ {{{log }_{0.5}}left( {{x^2} – 5x + 6} right) + 1} right] = 0$ là : A. 1 B. 3 C. 0 D. 2 Bài 3-[THPT Lục Ngạn – Bắc Giang 2017] Phương trình ${3^{{x^2} – 2x – 3}} + {3^{{x^2} – 3x + 2}} = {3^{2{x^2} – 5x – 1}} + 1$ A. Có ba nghiệm thực phân biệt B. Vô nghiệm C. Có hai nghiệm thực phân biệt D. Có bốn nghiệm thực phân biệt Bài 4-[THPT HN Amsterdam 2017] Tìm số nghiệm của phương trình ${2^{frac{1}{x}}} + {2^{sqrt x }} = 3$ : A. B. 2 C. Vô số D. Không có nghiệm Bài 5-[THPT Nhân Chính – Hà Nội 2017] Cho phương trình $2{log _2}x + {log _{frac{1}{3}}}left( {1 – sqrt x } right) = frac{1}{2}{log _{sqrt 2 }}left( {x – 2sqrt x + 2} right)$. Số nghiệm của phương trình là ; A. 2 nghiệm B. Vô số nghiệm C. 1 nghiệm D. Vô nghiệm Bài 6-[Thi HK1 chuyên Nguyễn Du – Đắc Lắc năm 2017] Tìm số nghiệm của phương trình $log {left( {x – 2} right)^2} = 2log x + {log _{sqrt {10} }}left( {x + 4} right)$ A. 3 B. 2 C. 0 D. 1 BÀI TẬP TỰ LUYỆN Bài 1-[Chuyên Khoa Học Tự Nhiên 2017] Số nghiệm của phương trình $log {left( {x – 1} right)^2} = sqrt 2 $ là A. 2 B. 1 C. 0 D. Một số khác GIẢI Phương trình $ Leftrightarrow log {left( {x – 1} right)^2} – sqrt 2 = 0$ . Sử dụng chức năng MODE 7 để tìm số nghiệm với Start -9 End 10 Step 1 Ta thấy có hai khoảng đổi dấu $ Rightarrow $ Phương trình ban đầu có 2 nghiệm $ Rightarrow $ A là đáp án chính xác Chú ý : Để tránh bỏ sót nghiệm ta thường thử thêm 1 hoặc 2 lần nữa với hai khoảng Start End khác nhau Ví dụ Start -29 End -10 Step 1 hoặc Sart 11 End 30 Step 1. Ta thấy không có khoảng đổi dấu nào nữa $ Rightarrow $ Chắc ăn hơn với 2 nghiệm tìm được

Bài 2-[THPT Lục Ngạn – Bắc Giang 2017] Số nghiệm của phương trình $left( {x – 2} right)left[ {{{log }_{0.5}}left( {{x^2} – 5x + 6} right) + 1} right] = 0$ là : A. 1 B. 3 C. 0 D. 2 GIẢI Tìm điều kiện của phương trình : ${x^2} – 5x + 6 > 0$ $ Leftrightarrow left[ begin{array}{l} x > 3\ x < 2 end{array} right.$ Phương trình $left( {x – 2} right)left[ {{{log }_{0.5}}left( {{x^2} – 5x + 6} right) + 1} right] = 0$ . Vì điều kiện chia hai khoảng nên ta MODE 7 hai lần. Lần thứ nhất với Start -7 End 2 Step 0.5 Ta thấy có 1 nghiệm x=1 Lần thứ hai với Start 3 End 12 Start 0.5 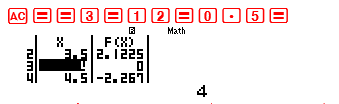Ta lại thấy có nghiệm x=4 $ Rightarrow $ Phương trình có 2 nghiệm 1 và 4 . $ Rightarrow $ Đáp án chính xác là D

Bài 3-[THPT Lục Ngạn – Bắc Giang 2017] Phương trình ${3^{{x^2} – 2x – 3}} + {3^{{x^2} – 3x + 2}} = {3^{2{x^2} – 5x – 1}} + 1$ A. Có ba nghiệm thực phân biệt B. Vô nghiệm C. Có hai nghiệm thực phân biệt D. Có bốn nghiệm thực phân biệt GIẢI Phương trình $ Leftrightarrow {3^{{x^2} – 2x – 3}} + {3^{{x^2} – 3x + 2}} – {3^{2{x^2} – 5x – 1}} – 1 = 0$ . Sử dụng MODE 7 với Start -9 End 0 Step 0.5 Ta thấy có 1 nghiệm x=-1 Tiếp tục MODE 7 với Start 0 End 9 Step 0.5 Ta lại thấy có thêm ba nghiệm x=1;2;3 $ Rightarrow $ Tổng cộng 4 nghiệm $ Rightarrow $ Đáp án chính xác là D

Bài 4-[THPT HN Amsterdam 2017] Tìm số nghiệm của phương trình ${2^{frac{1}{x}}} + {2^{sqrt x }} = 3$ : A. 1 B. 2 C. Vô số D. Không có nghiệm GIẢI Phương trình $ Leftrightarrow {2^{frac{1}{x}}} + {2^{sqrt x }} – 3 = 0$ (điều kiện $x ge 0$). Sử dụng MODE 7 với Start 0 End 4.5 Step 0.25 Trên đoạn $left[ {0;4.5} right]$ không có nghiệm nào Tiếp tục MODE 7 với Start $4.5$ End 9 Step 0.25 Dự đoán phương trình vô nghiệm. Để chắn ăn hơn ta thử lần cuối với Start 9 End 28 Step 1 Giá trị của F(X) luôn tăng đến $ + propto $ $ Rightarrow $ Phương trình vô nghiệm $ Rightarrow $ Đáp án chính xác là D Bài 5-[THPT Nhân Chính – Hà Nội 2017] Cho phương trình $2{log _2}x + {log _{frac{1}{3}}}left( {1 – sqrt x } right) = frac{1}{2}{log _{sqrt 2 }}left( {x – 2sqrt x + 2} right)$. Số nghiệm của phương trình là ; A. 2 nghiệm B. Vô số nghiệm C. 1 nghiệm D. Vô nghiệm GIẢI Phương trình $ Leftrightarrow 2{log _2}x + {log _{frac{1}{3}}}left( {1 – sqrt x } right) – frac{1}{2}{log _{sqrt 2 }}left( {x – 2sqrt x + 2} right) = 0$ (điều kiện $0 le x le 1$). Sử dụng MODE 7 với Start 0 End 1 Step 0.1 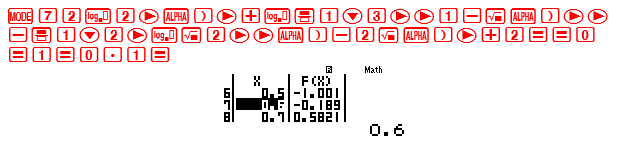Ta thấy có 1 nghiệm duy nhất thuộc khoảng $left( {0.6;0.7} right)$ $ Rightarrow $ Đáp án chính xác là C Bài 6-[Thi HK1 chuyên Nguyễn Du – Đắc Lắc năm 2017] Tìm số nghiệm của phương trình $log {left( {x – 2} right)^2} = 2log x + {log _{sqrt {10} }}left( {x + 4} right)$ A. 3 B. 2 C. 0 D. 1 GIẢI Phương trình $ Leftrightarrow log {left( {x – 2} right)^2} – 2log x – {log _{sqrt {10} }}left( {x + 4} right) = 0$ (điều kiện $x ge 0$). Sử dụng MODE 7 với Start 0 End 4.5 Step 0.25 Trên đoạn $left[ {0;4.5} right]$ có 1 nghiệm Tiếp tục MODE 7 với Start 4.5 End 9 Step 0.25 Trên khoảng này không thu được nghiệm nào. Để chắn ăn hơn ta thử lần cuối với Start 9 End 28 Step 1 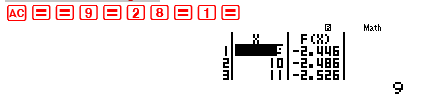Cũng không thu được nghiệm $ Rightarrow $ Tóm lại phương trình có nghiệm duy nhất $ Rightarrow $ Đáp án chính xác là C.

Healthy4life