Công thức tính đường cao trong tam giác thường, vuông, đều, cân từ A- Z

Trong bài viết dưới đây, THPT CHUYÊN LAM SƠN sẽ chia sẻ lý thuyết và công thức tính đường cao trong tam giác thường, vuông, đều và cân kèm theo các dạng bài tập có lời giải chi tiết để các bạn cùng tham khảo nhé.

Đường cao trong tam giác là gì?

Đường cao trong tam giác là đường thẳng từ đỉnh tam giác hạ vuông góc xuống cạnh đối diện. Trong một tam giác có 3 đường cao và chúng đồng quy với nhau tại 1 điểm.

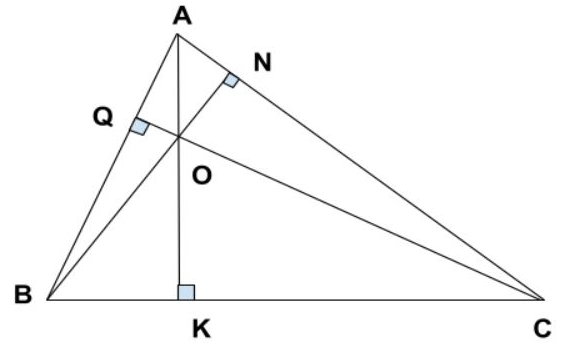
Công thức tính đường cao trong tam giác thường

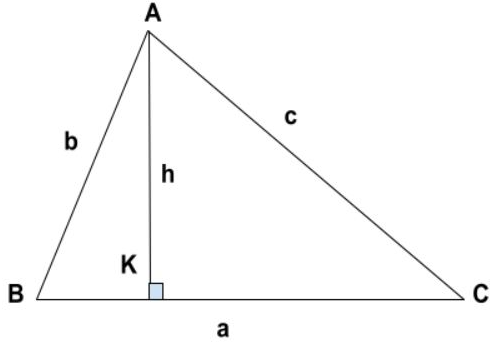
Cách tính đường cao của một tam giác bằng diện tích tam giác nhân 2 rồi chia cho cạnh đáy tương ứng với chiều cao đó

h = S.a

Trong đó:

• S: Diện tích của hình tam giác.
• a: Cạnh đáy tương ứng với chiều cao của hình tam giác.
• h: Chiều cao của tam giác.

Cách tính đường cao của một tam giác ta có thể sử dụng công thức Heron đã được chứng minh:

ha = 2.[√p.(p – a)(p – p)(p – c)]/2

Trong đó:

• h: Chiều cao của tam giác.
• b. c: Độ dài các cạnh của hình tam giác.
• a: Cạnh đáy tương ứng với chiều cao của hình tam giác
• p: Nửa chu vi của hình tam giác.

Ví dụ: Giả sử các bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như sau:Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH kể từ A cắt BC tại H và tính diện tích ABC.

Lời giải

Nửa chu vi tam giác : P = ( AB+BC+AC):2 = ( 4+7+5):2 = 8 cm

Xét tam giác ABC ta có:

SABC= ½AH.BC = ½4√8.7 = 14√8 cm2

Như vậy, AH = 4√8 cm, SABC = 14√8 cm2

Tham khảo thêm:

• Tam giác đều là gì ? Định nghĩa và tính chất của tam giác đều
• Tam giác cân là gì ? Định nghĩa và tính chất tam giác cân
• Công thức tính diện tích tam giác vuông, cân, đều chính xác

Công thức tính đường cao trong tam giác vuông

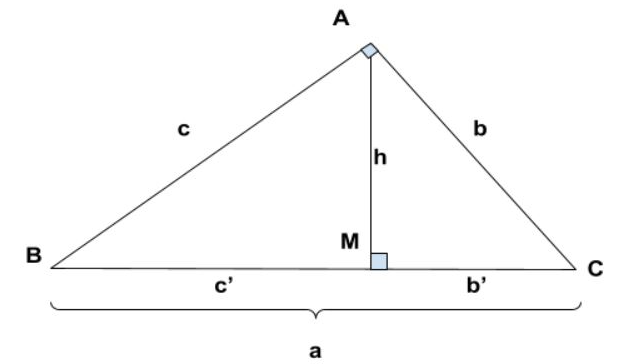
Áp dụng công thức tính cạnh và đường cao trong tam giác vuông, ta có công thức tính đường cao trong tam giác vuông là:

• a2 = b2 + c2
• b2 = a.b′ và c2 = a.c′
• a.h = b.c
• h2 = b′.c′
• 1/h2=1/b2+1/c2

Trong đó:

• a, b, c: độ dài các cạnh của tam giác vuông.
• b’: đường chiếu của cạnh b ứng trên cạnh huyền.
• c’: đường chiếu của cạnh c ứng trên cạnh huyền.
• h: đường cao hạ từ đỉnh góc vuông.

Ví dụ: Cho tam giác ABC vuông tại A, có đường cao AH, biết AB : AC = 3; AB + AC = 21cm.

a. Tính độ dài các cạnh của tam giác ABC.

b. Tính đường cao AH.

Lời giải

Theo giả thiết: AB:AC = 3:4

AB/AC = 3/4 ⇔ AB = 3AC/4

Trong khi: AB + AC = 21 ⇔ 3AC/4 + AC = 21⇔ AC = 12 cm

⇒ AB = 9 cm

Theo định lý pytago: BC2 = AB2 + AC2 = 92 + 122 = 225

⇒ BC = 15 cm

Như vậy AB = 9 cm, BC = 15 cm, AC = 12 cm

b. Tam giác vuông ABC vuông tại A nên ta có:

AH.BC = AB.AC

AH = (AB.AC)/BC = (9.12)/15 = 7,2 cm

Như vậy đường cao AH = 7,2 cm

Công thức tính đường cao trong tam giác đều

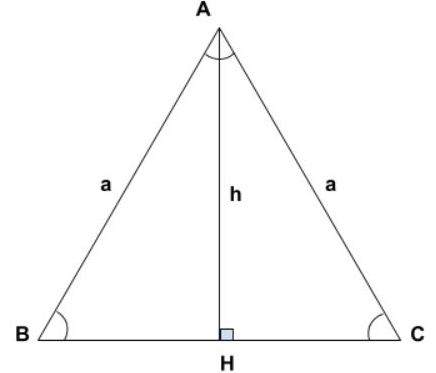
Đường cao tam giác đều có độ dài bằng nhau, áp dụng định lý Heron ta có công thức tính đường cao trong tam giác đều

h = a√3/2

Trong đó:

• h: Chiều cao của tam giác đều.
• a: Cạnh của tam giác đều.

Công thức tính đường cao trong tam giác cân

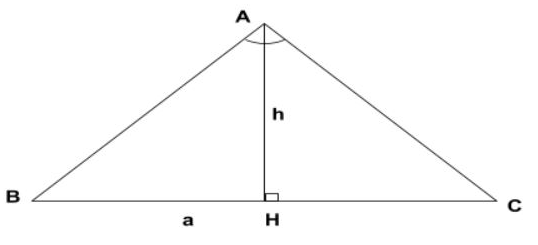
Ta có a là độ dài 2 cạnh băng nhau của tam giác cân, b là độ dài cạnh còn lại, ha là độ dài đường cao trong tam giác cân

Áp dụng định lý Pytago ta có: a2 = (b/2)2 + h2

Từ đó ta có công thức tính đường cao của tam giác cân là

h2 = a2 – (b/2)2 ⇒ h = √[a2 – (b/2)2]

Ví dụ: Tính chiều dài đường cao trong tam giác cân có độ dài 2 cạnh bằng nhau là 2cm và độ dài cạnh còn lại là 3

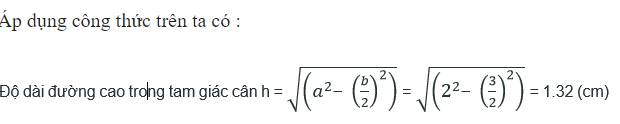
Hy vọng với những kiến trên về công thức tính đường cao trong tam giác thường, vuông, cân, đều có thể giúp bạn áp dụng vào làm bài tập nhanh chóng