Công thức Diện tích hình Thang & Cách tính đơn giản 2023

Diện tích hình thang gần giống như diện tích hình tam giác với cách tính tương đối đơn giản, nó đã trở thành công thức cần nắm chung cho các bạn học sinh lớp 5. Vậy hình chữ thang là gì và cách tính của nó ra sao?

Ngay sau đây, đội ngũ INVERT chúng tôi sẽ hướng dẫn bạn biết hình thang là gì, công thức tính diện tích hình thang & cách sử dụng nó vô cùng chi tiết, dễ hiểu thông qua bài viết sau.

I. Hình thang là gì? Diện tích hình thang là gì?

Hình thang trong hình học Euclide là 1 tứ giác lồi có 2 cạnh đối song song. Hai cạnh song song này được gọi là các cạnh đáy của hình thang và 2 cạnh còn lại gọi là 2 cạnh bên

Diện tích hình thang là toàn bộ phần mặt phẳng được giới hạn bên trong 4 cạnh bên mà chúng ta có thể nhìn thấy.

Ngoài ra, hình thang còn có các dạng đặc biệt khác như:

• Hình thang vuông là hình thang có một góc vuông.
• Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
• Hình bình hành là hình thang có 2 cạnh đáy bằng nhau và 2 cạnh bên song song và bằng nhau.
• Hình chữ nhật là hình thang vừa vuông vừa cân.

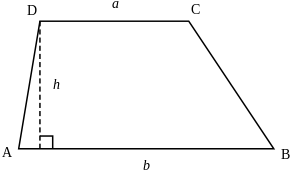
II. Công thức tính diện tích hình thang

Diện tích hình thang được tính bằng tổng độ dài hai đáy nhân với chiều cao rồi đem chia cho 2 (cùng một đơn vị đo).

Công Thức Chung: S = h x ((a + b)/2)

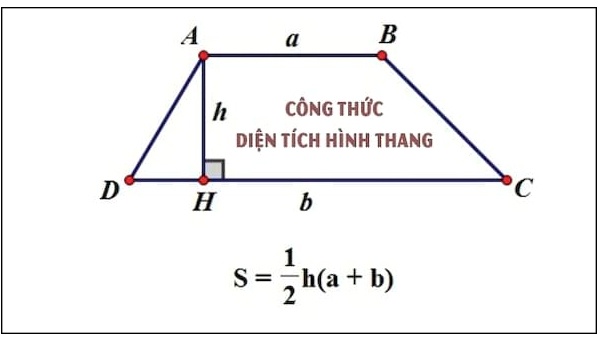
Trong đó:

• S: diện tích hình thang.
• h: chiều cao nối từ đỉnh tới đáy của hình thang.
• a và b: hai cạnh đáy của hình thang.

Công thức tính diện tích hình thang vuông

Hình thang vuông được biết là hình có 1 góc vuông và cạnh bên thường vuông góc với 2 đáy (chiều cao h)

Diện tích hình thang vuông được tính bằng trung bình cộng với 2 cạnh đáy và nhân với chiều cao giữa 2 đáy (chiều cao là cạnh bên vuông góc với 2 đáy).

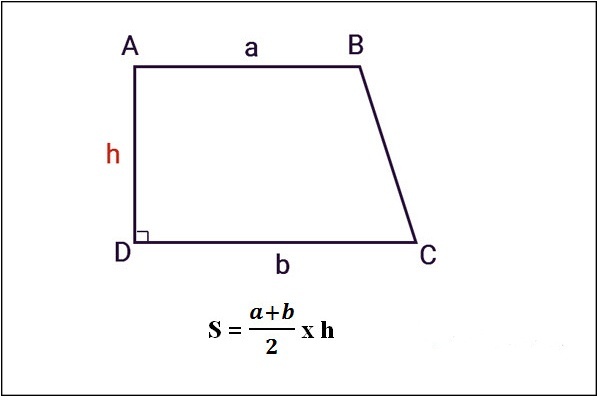
Trong đó:

• S: diện tích hình thang.
• h: độ dài cạnh bên vuông góc với 2 đáy
• a và b: độ dài 2 cạnh đáy của hình thang.

Công thức tính diện tích hình thang cân

Hình thang cân là hình thang có 2 góc kề 1 đáy bằng nhau và 2 cạnh bên bằng nhau, chúng thường không song song với nhau.

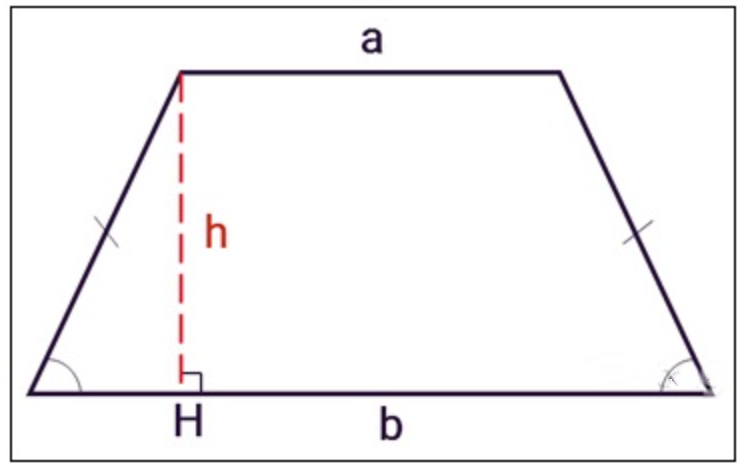
Nếu áp dụng công thức tính diên tích, bạn cũng có thể chia nhỏ ra để tính diện tích từng phần và cộng lại với nhau

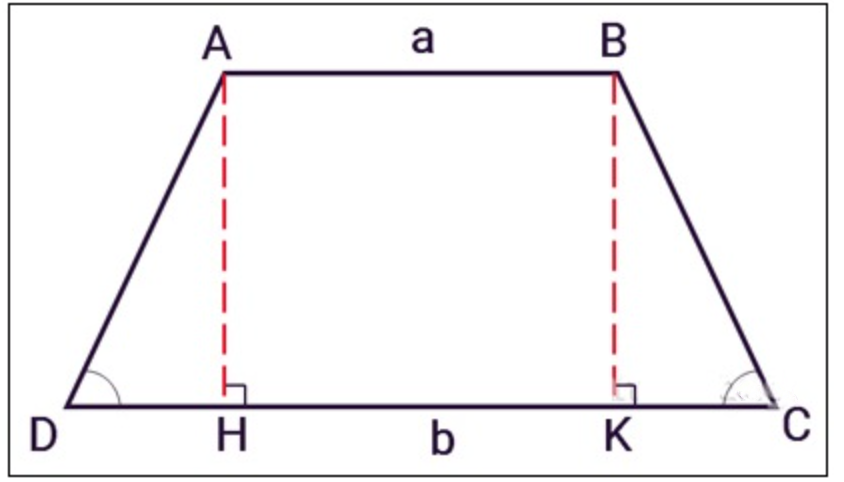
Công thức tính chiều cao hình thang, đáy lớn, đáy nhỏ hình thang

Qua những công thức hình thang ở trên, bạn cũng có thể dễ dàng giải các bài tập nâng cao về hình thang như tính chiều cao khi biết diện tích hình thang hay tính đáy lớn, đáy nhỏ khi biết diện tích như sau:

* Công thức tính chiều cao hình thang khi biết diện tích, chiều dài 2 cạnh

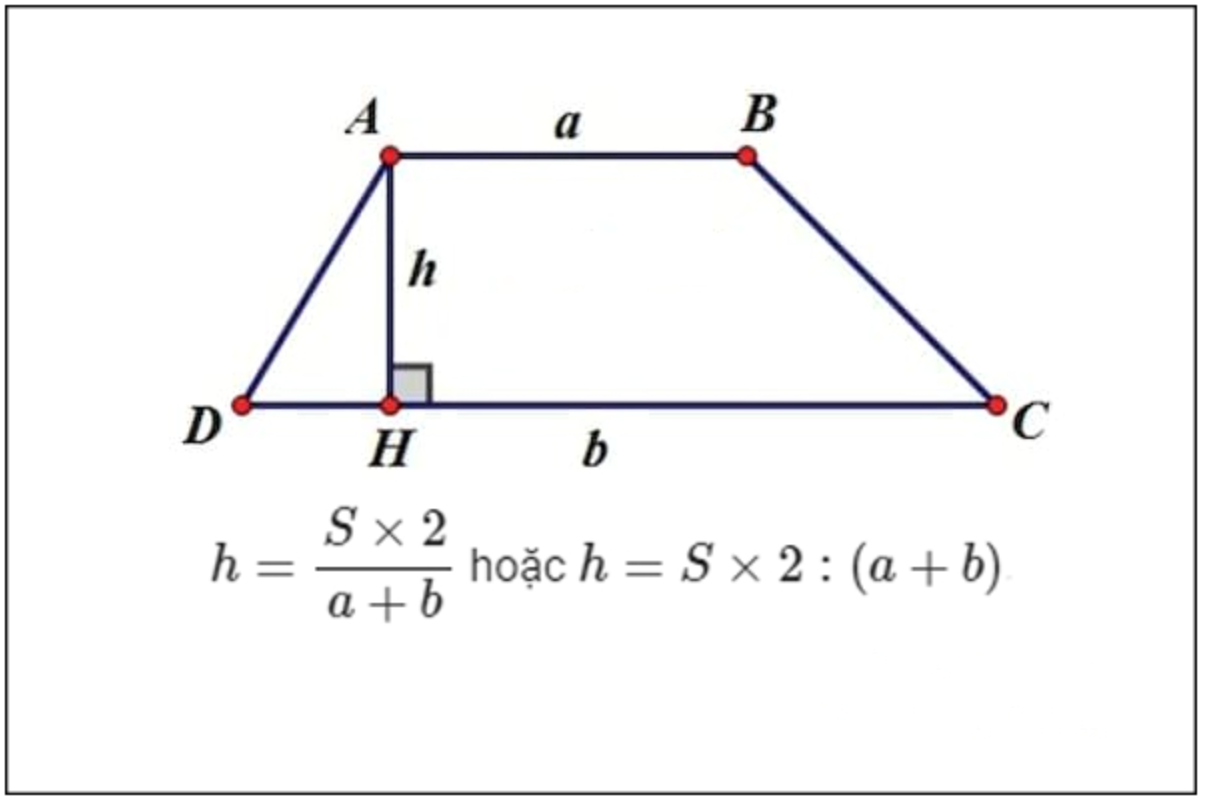
* Công thức tính tổng hai đáy của hình thang khi biết diện tích, chiều cao

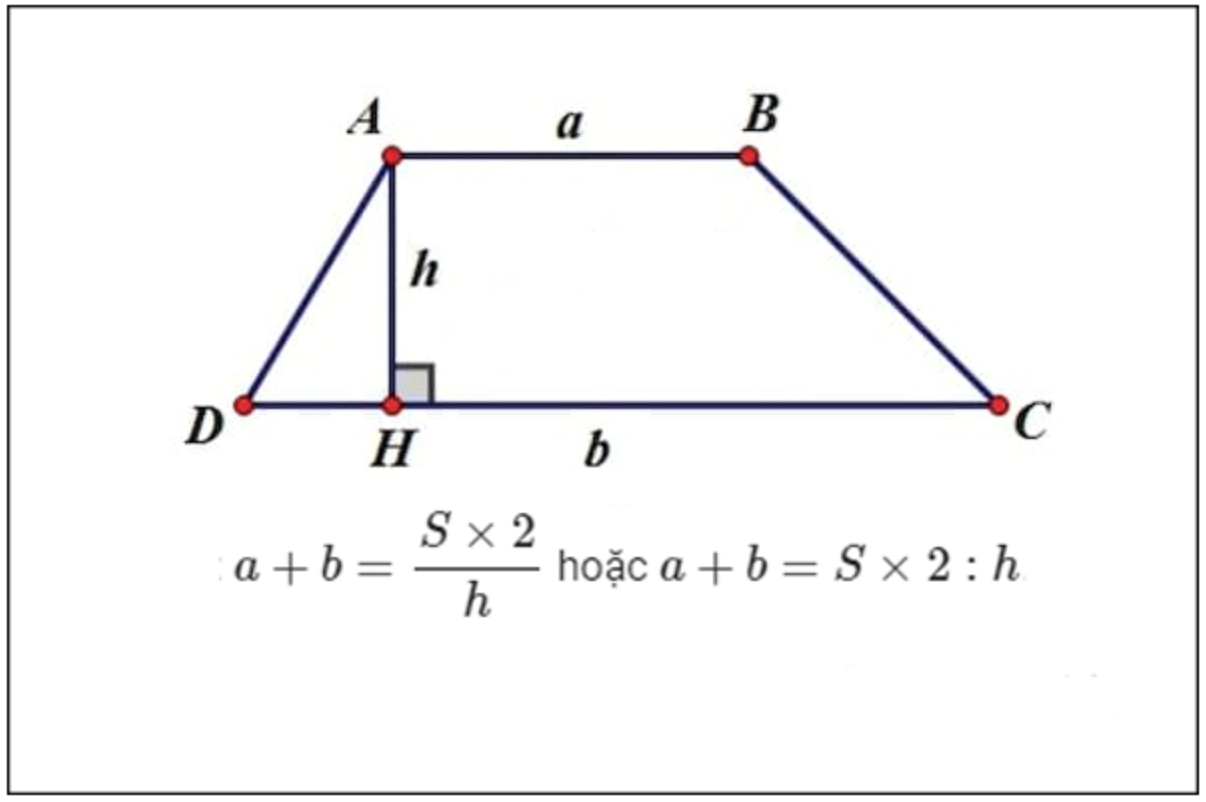
III. Hướng dẫn cách tính diện tích hình thang

1. Tính diện tích với chiều cao và độ dài 2 cạnh đáy

Bước 1: Tính tổng độ dài 2 cạnh đáy

Vì đáy của hình thang là 2 cạnh song song với nhau nên nếu đề bài không cho sẵn độ dài 2 đáy, bạn hãy dùng thước để đo từng giá trị. Rồi bạn cộng 2 độ dài này lại với nhau để tính tổng.

Giả sử: Cho hình thang có độ dài đáy trên là (b1) = 8 cm và đáy dưới (b2) = 13 cm, ta có tổng độ dài 2 đáy là: “b = b1 + b2” = 8 cm + 13 cm = 21 cm.

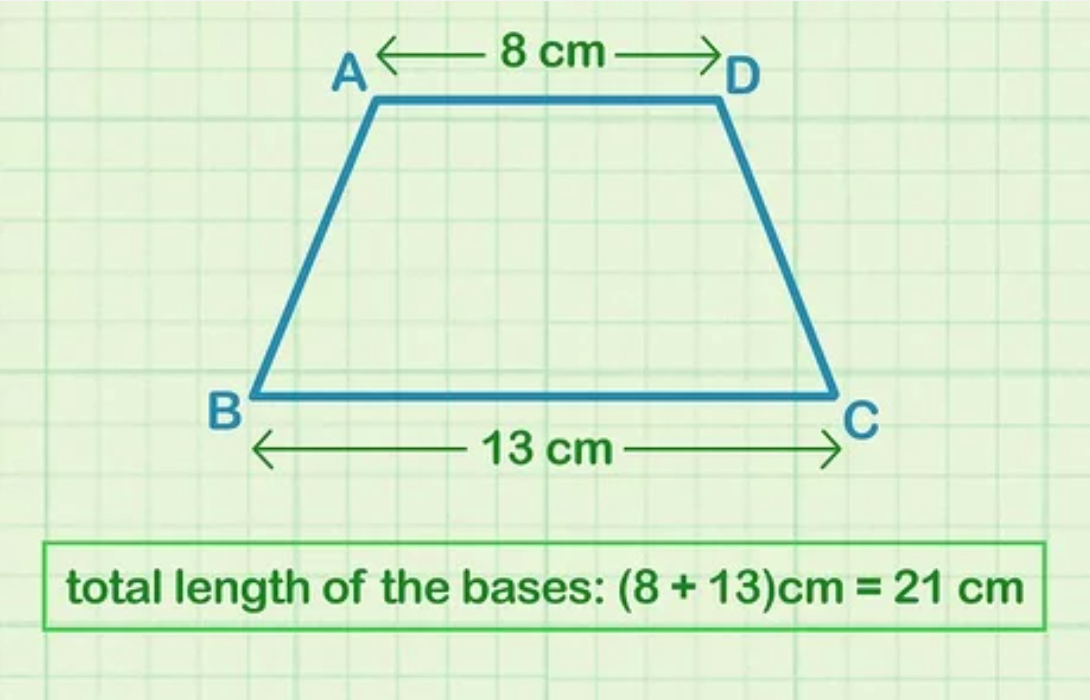
Bước 2: Tính chiều cao của hình thang

Trong hình thang, chiều cao là khoảng cách giữa 2 đáy song song nên bạn hãy vẽ 1 đường thẳng từ đáy trên xuống đáy dưới sao cho vuông góc với 2 cạnh đáy. Sau đó, bạn dùng thước hoặc dụng cụ đo khác để xác định độ dài. Rồi tiến hành ghi lại giá trị chiều cao để sử dụng sau đó.

Lưu ý: Độ dài của 2 cạnh bên không phải là chiều cao của hình thang và nó chỉ xảy ra với hình thang vuông.

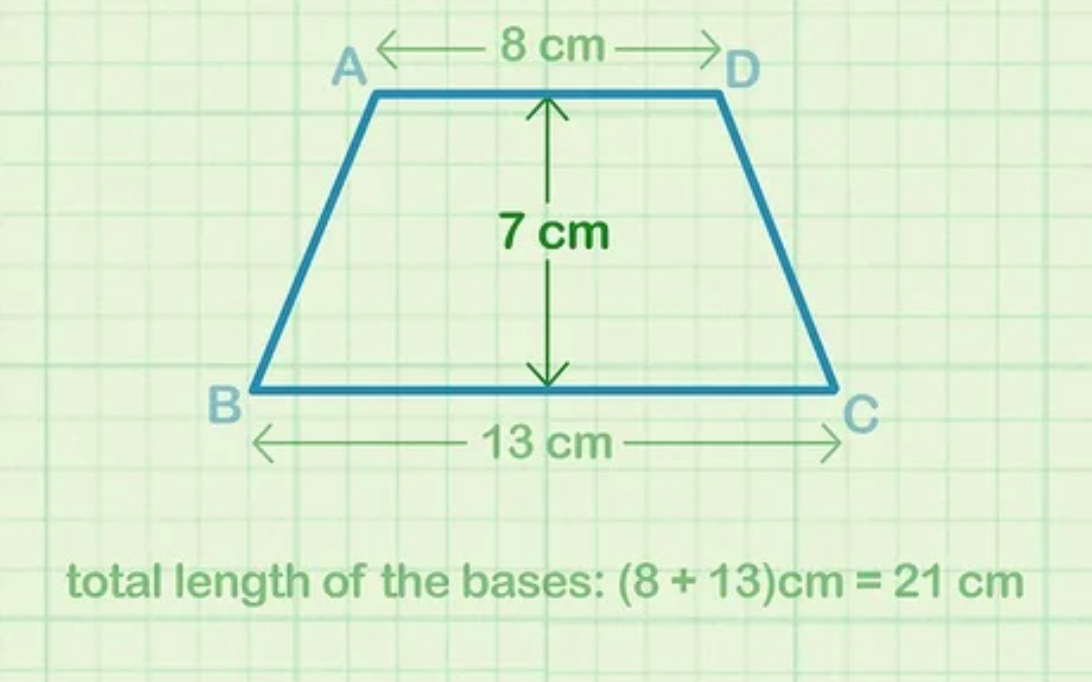
Bước 3: Lấy tổng độ dài 2 đáy nhân với chiều cao

Sau khi đã có chiều cao, bạn lấy tổng 2 đáy (b) mà bạn đã tính nhân với chiều cao (h). Nhớ thêm ký hiệu bình phương vào đơn vị độ dài của kết quả.

Theo ví dụ trên: Ta có “(b)h” = 21 cm x 7 cm = 147 cm2.

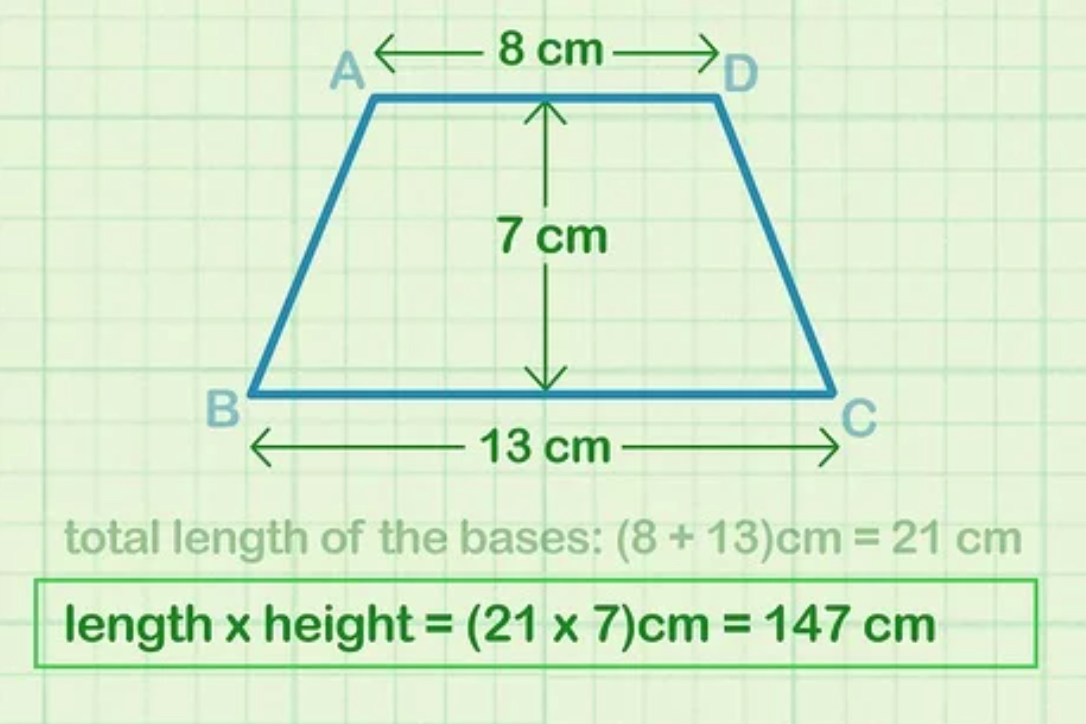
Bước 4: Lấy tích của tổng 2 đáy và chiều cao nhân với ½ (hoặc chia 2) để tìm diện tích hình thang

Để tính diện tích hình thang, bạn tiến hành lấy tích của tổng 2 đáy và chiều cao nhân với ½ (hoặc chia 2 cũng ra cùng 1 kết quả). Đừng quên ghi đơn vị diện tích cho đáp án của bài toán.

Từ ví dụ trên: Ta có diện tích của hình thang S = 147 cm2 / 2 = 73,5 cm2

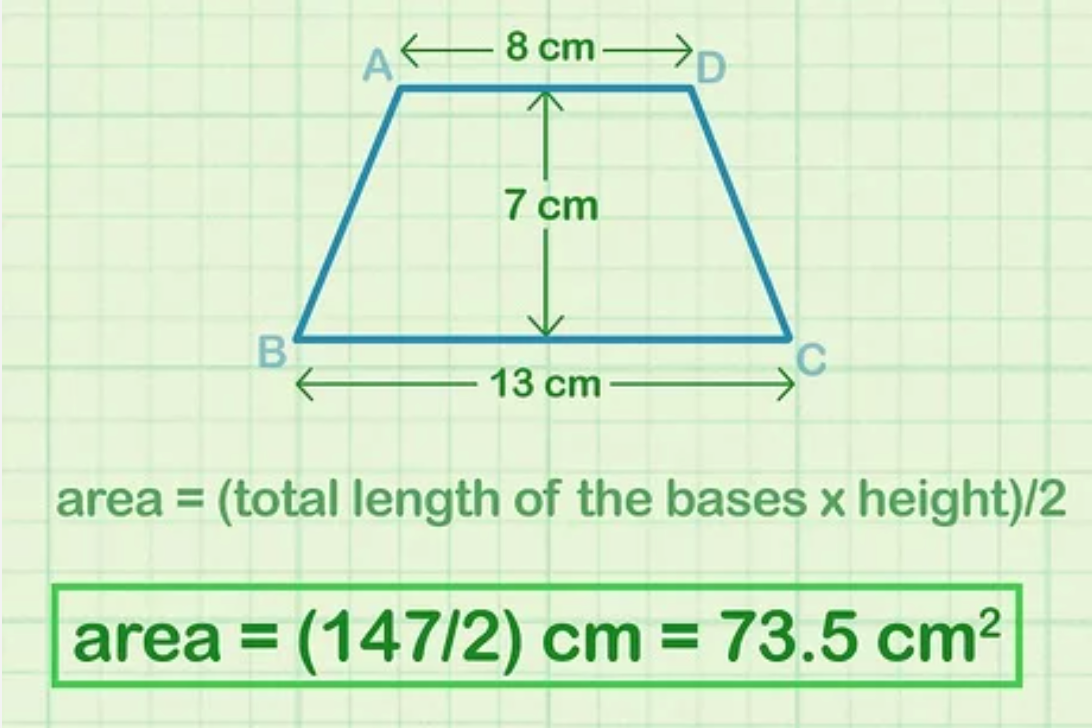
2. Tính diện tích của hình thang nếu biết độ dài cạnh bên

Bước 1: Chia hình thang thành 1 hình chữ nhật và 2 tam giác vuông

Trước tiên, bạn kẻ các đường thẳng từ góc của đáy trên cắt đáy dưới 1 góc 90º. Khi đó, hình thang sẽ có 1 hình chữ nhật ở giữa và 2 tam giác vuông với cạnh huyền bằng nhau nằm 2 bên. Tuy nhiên, phương pháp này chỉ áp dụng được với hình thang cân.

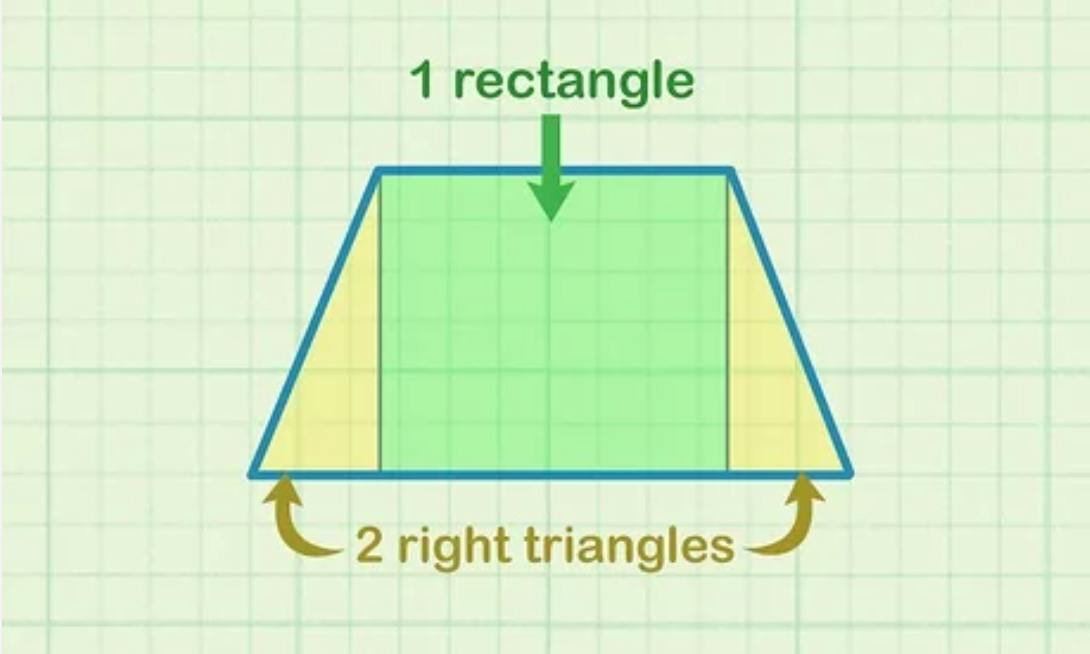
Bước 2: Tìm độ dài của cạnh đáy tam giác

Kế đó, bạn lấy độ dài đáy trên của hình thang trừ đi độ dài đáy dưới để tính khoảng cách còn lại. Sau đó, bạn tiếp tục lấy khoảng cách này chia 2 để tìm độ dài cạnh đáy của tam giác. Khi đó, bạn sẽ có độ dài cạnh đáy và cạnh huyền của tam giác vuông.

Giả sử: Cho hình thang có đáy trên (b1) = 6 cm, đáy dưới (b2) = 12 cm, gọi A là cạnh đáy của hình tam giác, ta có A = (b2 – b1)/2 = (12 cm – 6 cm)/2 = 3 cm.

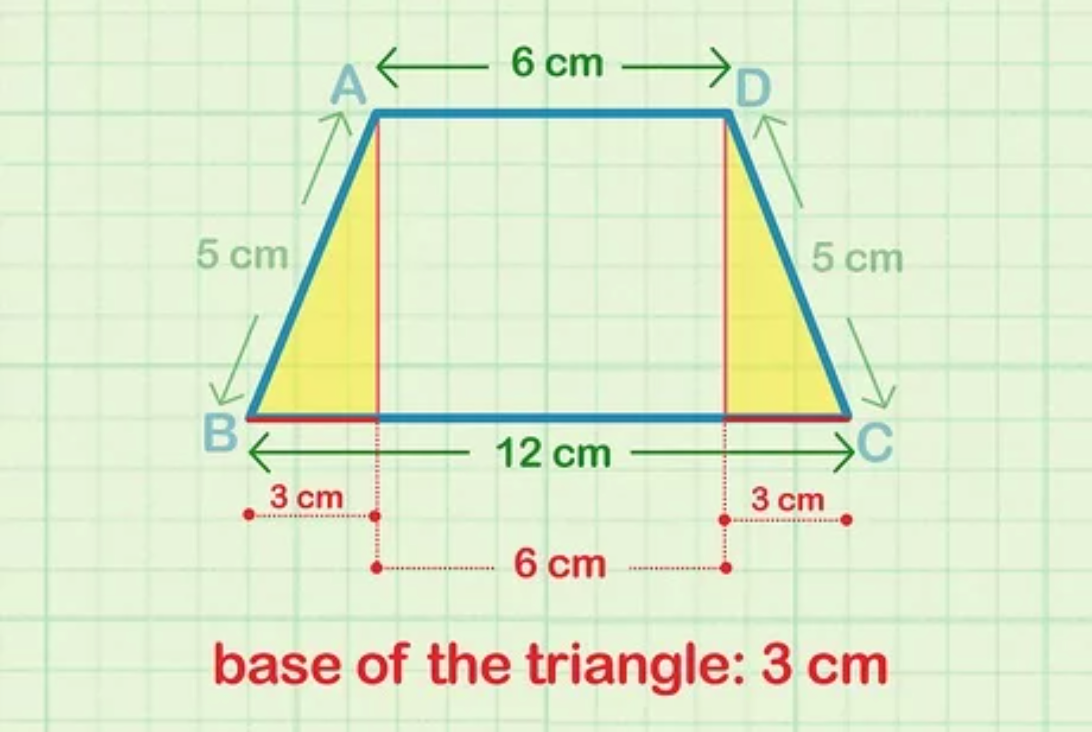
Bước 3: Sử dụng định lý Pytago để tìm chiều cao của hình thang

Sau khi đã có giá trị độ dài cạnh đáy và cạnh huyền (cạnh dài nhất trong tam giác vuông), hãy vào công thức A2 + B2 = C2. Trong đó A là cạnh đáy còn C là cạnh huyền.

Bạn tiến hành giải phương trình để tìm B. Khi đó, bạn sẽ có được chiều cao của hình thang.

Giả sử: Nếu độ dài cạnh đáy của tam giác vuông mà bạn tìm được là 3 cm và cạnh huyền là 5 cm thì khi thay vào công thức, bạn sẽ có phương trình:

• (3 cm)2 + B2 = (5 cm)2
• Bình phương các giá trị: 9 cm +B2 = 25 cm
• Lấy cả hai vế phương trình trừ đi 9: B2 = 16 cm
• Tính căn bậc hai của hai vế: B = 4 cm

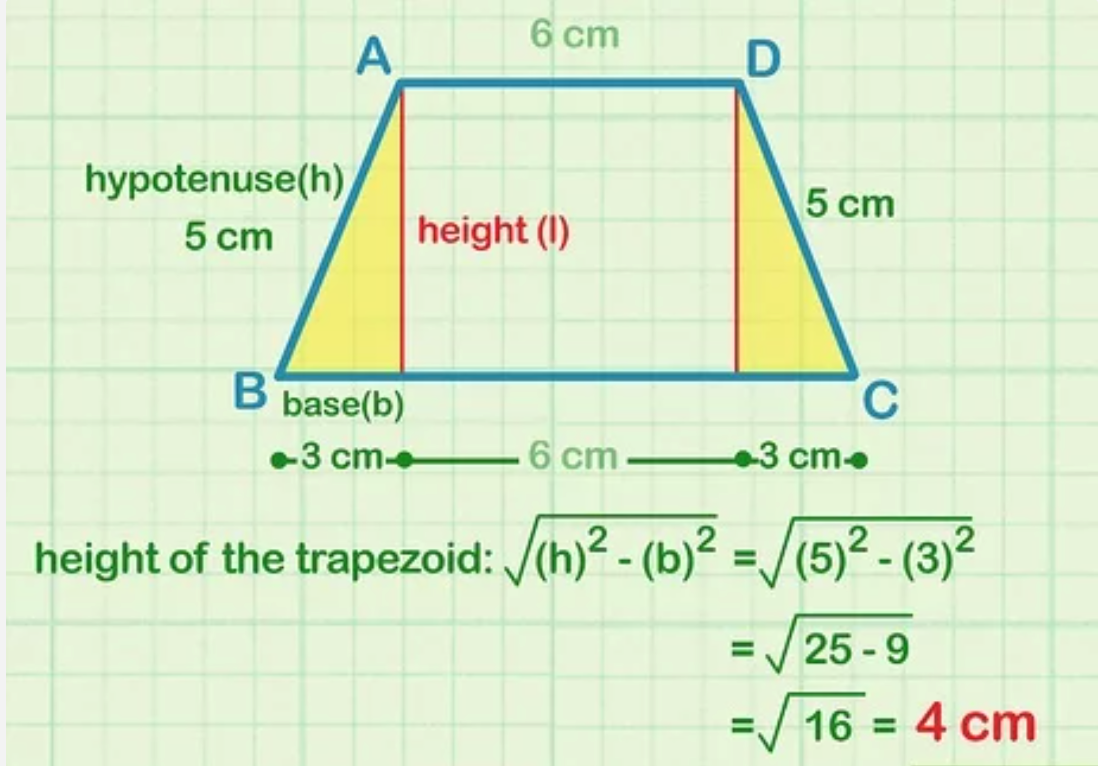
Bước 4: Thay độ dài 2 đáy và chiều cao vào công thức tính diện tích

Cuối cùng, bạn thay độ dài 2 đáy và chiều cao vào công thức diện tích hình thang S = ½(b1 +b2)h. Sau đó, rút gọn biểu thức đến mức tối giản, thêm đơn vị diện tích cho đáp án.

• Công thức: S = ½(b1+b2)h
• Thay các giá trị : S = ½(6 cm +12 cm)(4 cm)
• Rút gọn biểu thức: S = ½(18 cm)(4 cm)
• Nhân các số hạng với nhau: S = 36 cm2.

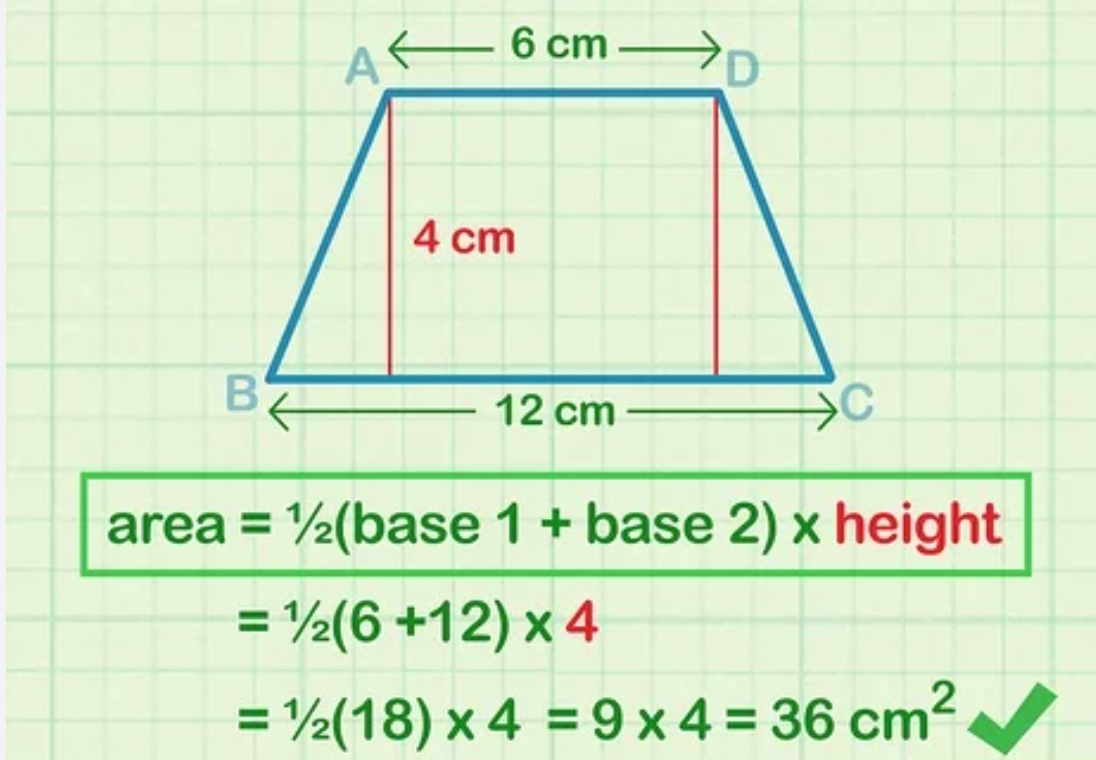
IV. Một số bài tập tính diện tích hình thang

1. Bài tập tính diện tích hình thang có lời giải

Câu 1: Tính diện tích mỗi hình thang đã cho dưới đây với số đo trên hình vẽ:

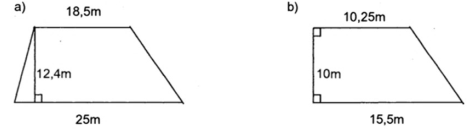
Giải:

a) Diện tích hình thang là: (18,5 + 25) x 12,4 : 2 = 269,7m²

b) Diện tích hình thang là: (10,25 + 15,5) x 10 : 2 = 128,75m²

Câu 2: Một hình thang có chiều cao bằng 56cm. Đáy lớn hơn đáy bé 24cm và đáy bé bằng 2/5 đáy lớn. Tính diện tích hình thang.

Giải:

Hiệu số phần bằng nhau là: 5 – 2 = 3 (phần)

Độ dài đáy lớn là: 24 : 3 x 5 = 40 (cm)

Độ dài đáy bé là: 40 – 24 = 16 (cm)

Diện tích hình thang là: (16 + 40) x 56 : 2 = 1568 (cm2)

Đáp số: 1568cm2

Câu 3: Cho hình thang có tổng độ dài hai đáy bằng 24 cm, đáy lớn hơn đáy bé 1,2 cm, chiều cao kém đáy bé 2,4 cm. Tính diện tích hình thang.

Giải:

Đáy bé là: (24 – 1,2) : 2 = 11,4cm

Chiều cao của hình thang là: 11,4 – 2,4 = 9cm

Diện tích của hình thang là: 24 x 9 : 2 = 108m²

Câu 4: Thửa ruộng hình thang có trung bình cộng hai đáy là 46 m. Nếu mở rộng đáy lớn thêm 12 m và giữ nguyên đáy bé thì thì được thửa ruộng mới có diện tích lớn hơn diện tích thửa ruộng ban đầu là 114 m². Tính diện tích thửa ruộng ban đầu?

Giải:

Tổng hai đáy là: 46 x 2 = 92m

Goi chiều cao thửa ruộng là h

Diện tích thửa ruộng ban đầu là: 92 x h : 2 = 46 x h

Tổng đáy lớn và đáy bé sau khi mở rộng đáy lớn thêm 12m là: 92 + 12 = 104m

Diện tích thửa ruộng sau khi mở rộng đáy lớn là: 104 x h : 2 = 52 x h

Thửa ruộng mới có diện tích mới lớn hơn 114m²

⇒ 52 x h – 46 x h = 114 hay h = 19m

Diện tích thửa ruộng ban đầu là: 46 x 19 = 874m²

Câu 5: Một thửa ruộng hình thang có đáy lớn 120 m, đáy bé bằng 2/3 đáy lớn và bằng 4/3 chiều cao. Người ta trồng ngô trên thửa ruộng đó, tính ra trung bình 100 m2 thu được 50 kg ngô. Hỏi cả thửa ruộng thu được bao nhiêu tạ ngô?

Giải:

Đáy bé là: 120 x 2 : 3 = 80m

Chiều cao là: 80 x 3 : 4 = 60m

Diện tích của thửa ruộng hình thang là: (120 + 80) x 60 : 2 = 6000m²

Số kg ngô thu được là: 6000 : 50 = 120kg

Đổi 120kg = 1,2 tạ

Câu 6: Tính diện tích hình thang biết:

a) Độ dài hai đáy lần lượt là 12 cm và 8 cm; chiều cao là 5 cm.

b) Độ dài hai đáy lần lượt là 9,4 m va 6,6m; chiều cao là 10,5 m

Giải:

a) Diện tích hình thang là: S = (12 + 8) × 52 = 50 cm2. Đáp số : 50cm2

b) Diện tích hình thang là: S = (9,4 + 6,6) x 10,5 = 84. Đáp số : 84m2

Câu 7: Một thửa ruộng hình thang có độ dài hai đáy lần lượt là 110m và 90,2m. Chiều cao bằng trung bình cộng của hai đáy. Tính diện tích thửa ruộng đó.

Giải:

Chiều cao của thửa ruộng là: (110+90,2)2=100,1(m)

Diện tích thửa ruộng là:

S=(a+b)×h)/2=(110+90,2) × 100,1 / 2 = 200,2 × 100,1 / 2=10000,01 (m2)

Câu 8: Có một mảnh đất hình thang với đáy bé là 24m, đáy lớn là 30m. Mở rộng hai đáy về phía bên phải của mảnh đất với đáy lớn thêm 7m, đáy nhỏ thêm 5m thu được mảnh đất hình thang mới với diện tích lớn hơn diện tích ban đầu là 36m2. Tính diện tích mảnh đất hình thang ban đầu.

Giải:

Chiều cao mảnh đất hình thang là: h = (36 x 2) : (7 + 5) = 6 m Diện tích mảnh đất ban đầu là: S = 6 . (24 + 30) : 2 = 162 m2.

Câu 9: Cho hình thang ABCD có cạnh AB = 5cm, cạnh CD = 9cm, chiều cao giữa hai cạnh đáy là 6cm. Tính diện tích hình thang ABCD.

Giải: Áp dụng công thức tính diện tích hình thang, ta có: SABCD = 6 . (5 + 9) : 2 = 42 (cm2).

Câu 10: Cho hình thang vuông có khoảng cách 2 đáy là 16cm, đáy nhỏ bằng ¾ đáy lớn. Tính độ dài 2 đáy khi biết được diện tích hình thang vuông là 112cm2.

Giải:

Khoảng cách 2 đáy trong hình thang vuông chính là chiều cao hình thang nên:

Tổng độ dài hai đáy là (112 x 2) : 16 = 14 (cm). Ta gọi độ dài đáy bé là a, độ dài đáy lớn là b, ta có: a + b = 14 và a = ¾ b. Thay vào ta có ¾ b +b = 14. Nên b = 14 : 7 x 4 = 8 (cm). => a = 14 – 8 = 6 (cm) Do đó, đáy bé là 6cm, đáy lớn 8cm.

2. Bài tập tính diện tích hình thang không có lời giải

Câu 1: Cho hình thang ABCD. Bốn điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Biết diện tích tứ giác MNPQ là 115 cm2. Tính diện tích hình thang ABCD.

Câu 2: Cho hình thang ABCD có độ dài đường cao là 4,2 dm, diện tích = 36,12 dm2 và đáy lớn CD dài hơn đáy bé AB là 7,8 dm. Kéo dài AD và BC cắt nhau tại E. Biết AD = 3/5 DE. Hỏi diện tích hình tam giác ABE là bao nhiêu?

Câu 3: Cho hình thang vuông ABCD (góc A, D là góc vuông) có AB=4cm, DC=5cm, AD=3cm. Nối D với B được hai hình tam giác ABD và BDC.

a) Tính diện tích hình tam giác đó.

b) Tính tỉ số phần trăm của diện tích hình tam giác ABD và diện tích hình tam giác BDC.

Câu 4: Tính chiều cao hình thang có:

a). Diện tích 30cm²; đáy lớn 8cm và đáy bé 0,4dm.

b). Diện tích 6,4 dm²; đáy lớn 1,8dm; đáy bé 1,4dm.

c). Diện tích 3/4m²; đáy lớn 1/4m và đáy bé 1/8m.

Câu 5: Tính diện tích hình thang có :

a). Đáy lớn 8m; đáy bé 75dm; chiều cao 32dm.

b). Đáy lớn 1,9m; đáy bé 1,3m; chiều cao 0,9m.

c). Đáy lớn 2/3m; đáy bé 1/2m; chiều cao 3/5m.

Câu 6: Tính tổng hai đáy hình thang có:

a). Diện tích 3,6 dam²; chiều cao 1,2dam.

b). Diện tích 3/4m²; chiều cao 2/3m.

c). Diện tích 2400cm²; chiều cao 3,8dm.

Câu 7: Một thửa ruộng hình thang vuông có cạnh bên vuông góc với 2 đáy dài 30,5m; đáy lớn 120,4m; đáy bé 79,6m.

a. Tính diện tích thửa ruộng bằng dam²

b. Trung bình 100dam2 thu được 65,2kg thóc. Hỏi trên cả thửa ruộng thu được bao nhiêu kg thóc?

Câu 8: Một hình thang có đáy bé 2,8dm.Đáy lớn bằng 7/3 đáy bé và bằng 5/3 chiều cao. Tính diện tích hình thang.

Câu 9: Một miếng đất hình thang có đáy bé 18m và bằng ¾ đáy lớn. Tính diện tích miếng đất hình thang?

Câu 10: Một thửa ruộng hình thang có đáy lớn 75,6m; đáy bé 62,4m và chiều cao 40m. Biết rằng 2/5 diện tích thửa ruộng trồng ngô, 1/3 diện tích trồng khoai, còn lại trồng đậu phộng. Tính diện tích trồng mỗi loại cây trên?

Trên đây là công thức Diện tích hình Thang & cách tính diện tích hình Thang đơn giản 2023, nhanh chóng mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể tính được diện tích hình Thang một cách dễ dàng. Nếu có gì thắc mắc bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc các bạn thành công.