Viết phương trình tiếp tuyến của đồ thị hàm số

Phương trình tiếp tuyến của đồ thị hàm số có rất nhiều dạng bài như: viết pttt của hàm số tại 1 điểm, đi qua 1 điểm, biết hệ số góc…Nhưng phần này lại không khó khăn gì nếu chúng ta nắm được phương pháp của từng dạng bài này.

I.Lý thuyết: Bài toán về tiếp tuyến với đường cong:

Cách 1: Dùng tọa độ tiếp điểm

Phương trình tiếp tuyến có dạng: y = f’(x0). (x – x0) + y0

1.Lập phương trình tiếp tuyến với đường cong tại điểm M(x0, y0) thuộc đồ thị hàm số (tức là tiếp tuyến duy nhất nhận M(x0; y0) làm tiếp điểm).

Phương trình tiếp tuyến với hàm số (C): y = f(x) tại điểm M(x0; y0) ∈ (C)

(hoặc tại h x = x0 ) có dạng: y =f’(x0).(x – x0) + y0.

2.Lập phương trình tiếp tuyến d với đường cong đi qua điểm A (xA, yA) cho trước, kể cả điểm thuộc đồ thị hàm số (tức là mọi tiếp tuyến đi qua A(xA, yA)).

Cho hàm số (C): y = f(x). Giả sử tiếp điểm là M(x0, y0), khi đó phương trình tiếp tuyến có dạng: y = f’(x).(x – x0) + y0 (d).

Điểm A(xA, yA) ∈ d, ta được: yA = f’(x0). (xA – x0) + y0 => x0

Từ đó lập được phương trình tiếp tuyến d.

3. Lập phương tiếp tuyến d với đường cong biết hệ số góc k

Cho hàm số (C): y = f(x). Giả sử tiếp điểm là M(x0;y0), khi đó phương trình tiếp tuyến có dạng: d: y = f’(x0).(x – x0) + y0.

Hoành độ tiếp điểm của tiếp tuyến d là nghiệm của phương trình:

f’(x0) = k => x0, thay vào hàm số ta được y0 = f(x0).

Ta lập được phương trình tiếp tuyến d: y = f’(x0). (x – x0) + y0.

Cách 2: Dùng điều kiện tiếp xúc

Phương trình đường thẳng đi qua một điểm M(x0; y0) có hệ số góc k có dạng;

d:y = g’(x) = k.(x – x0) + y0.

Điều kiện để đường thằng y = g(x) tiếp xúc với đồ thị hàm số y = f(x) là hệ phương trình sau có nghiệm: (left{begin{matrix} f(x)=g(x) & \ f'(x)=g'(x) & end{matrix}right.) Từ đó lập được phương trình tiếp tuyến d.

II. Bài tập

Loại 1: Cho hàm số y =f(x). Viết phương trình tiếp tuyến tại điểm M0(x0; y0) ∈ (C).

Giải

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)

Với x0 là hoành độ tiếp điểm;

Với y0 = f(x0) là tung độ tiếp điểm;

Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.

Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k.

MỘT SỐ DẠNG CƠ BẢN

Dạng 1: Viết phương trình tiếp tuyến tại M0(x0;y0) ∈ (C)

-Tính đạo hàm của hàm số, thay x0 ta được hệ số góc

Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.

Dạng 2: Cho trước hoành độ tiếp điểm x0

-Tính đạo hàm của hàm số, thay x0 ta được hệ số góc.

– Thay x0 vào hàm số ta tìm được tung độ tiếp điểm.

Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.

Dạng 3: Cho trước tung độ tiếp điểm y0

-Giải phương trình y0 = f(x0) để tìm x0.

-Tính đạo hàm của hàm số, thay x0 ta được hệ số góc.

Áp dụng (*) ta được phương trình tiếp tuyến cần tìm.

Chú ý: Có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.

Dạng 4: Cho trước hệ số góc của tiếp tuyến k = y’(x0) = f’(x0)

-Tính đạo hàm và giải phương trình k = y’(x0) = f’(x0) để tìm x0

– Thay x0 vào hàm số ta tìm được tung độ tiếp điểm cần tìm.

Chú ý: Có bao nhiêu giá trị của x0 thì có bấy nhiêu tiếp tuyến.

Chú ý: Một số dạng khác

-Khi giả thiết yêu cầu viết phương trình tiếp tuyến biết tiếp tuyến vuông góc với đường thẳng : y = ax + b thì điều này

<=> y’(x0). a = -1 ⇔ y’(x0) = -1/a

… Quay về dạng 4.

– Khi giả thiết yêu cầu viết phương trình tiếp tuyến biết tiếp tuyến song song với đường thẳng

y = ax + b thì điều này ⇔ y’(x0) = a… Quay về dạng 4.

– Khi giả thiết yêu cầu viết phương trình tiếp tuyến tại giao điểm với đường thẳng y = ax + b thì việc đầu tiên là tìm tọa độ giao điểm của (C) và đường thẳng… Quay về dạng 1.

Chú ý:

Cho hai đường thẳng d1: y = a1x + b1 với a1 là hệ số góc của đường thẳng d1 và y = a2x + b2 với a2 là hệ số góc của đường thẳng d2.

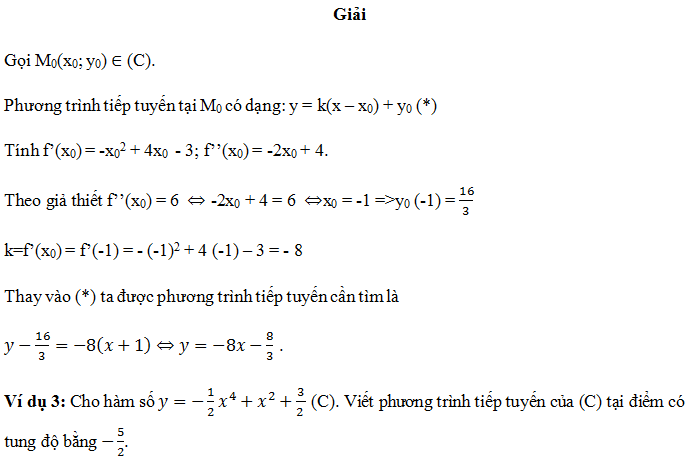
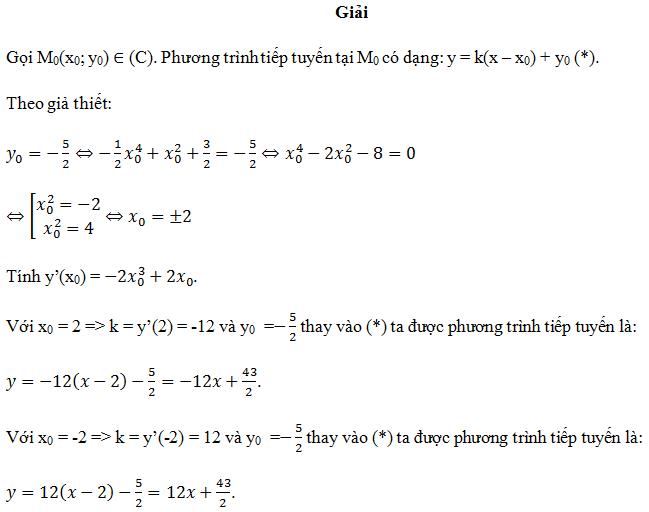
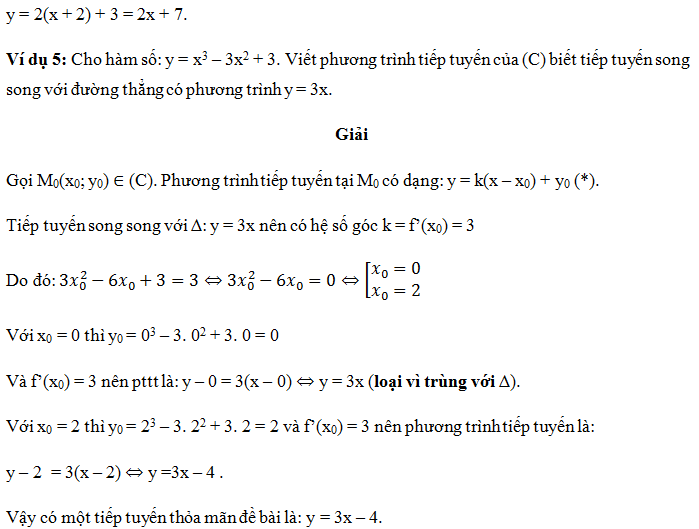
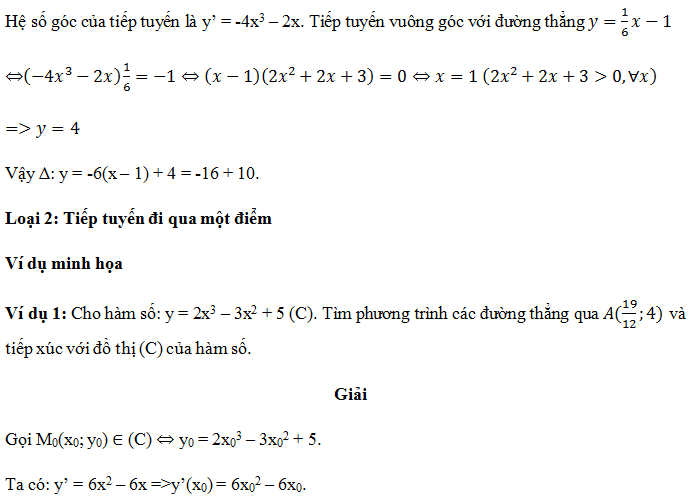
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:

Tải về

Luyện Bài tập trắc nghiệm môn Toán lớp 12 – Xem ngay