✅ Cách nhận dạng đồ thị hàm số ⭐️⭐️⭐️⭐️⭐️ – TRUNG TÂM GIA SƯ TÂM TÀI ĐỨC ⭐️

1. Dấu hiệu nhận biết (dấu âm dương) các hệ số của hàm bậc ba dựa vào đồ thị

Hàm số bậc 3 có dạng tổng quát: y = ax3 + bx2 + cx + d (a ≠ 0) (1)

Lấy đạo hàm (1): y’ = 3ax2 + 2bx + c

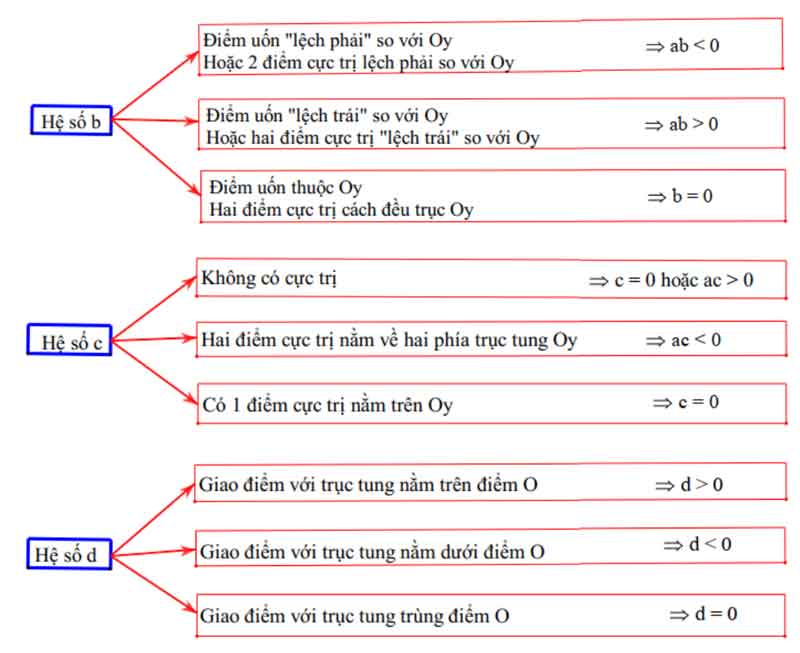
Dựa vào vị trị của 2 điểm cực trị so với trục Oy

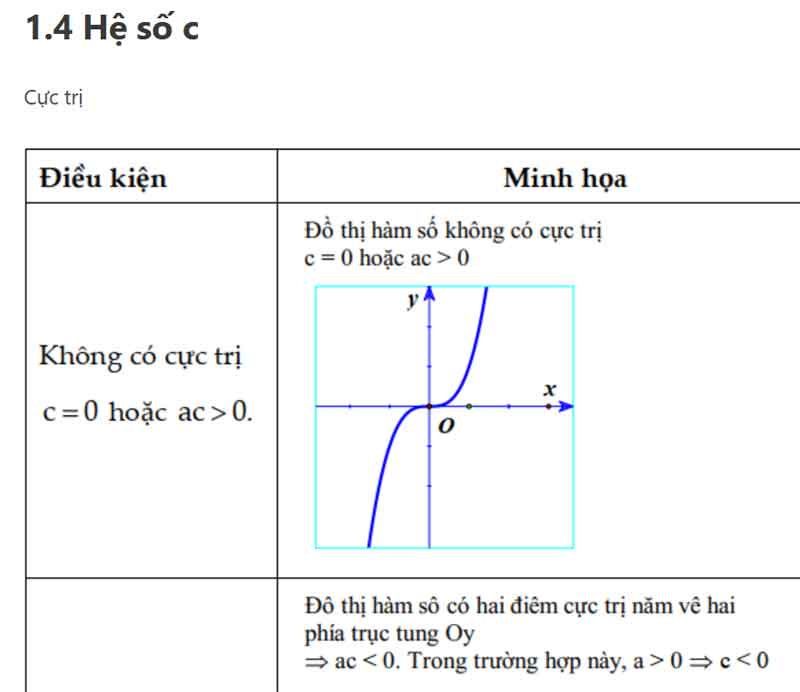
2. Đồ thị hàm bậc 4 trùng phương

Hàm số y = ax4 + bx2 + c ( với a ≠ 0) (2)

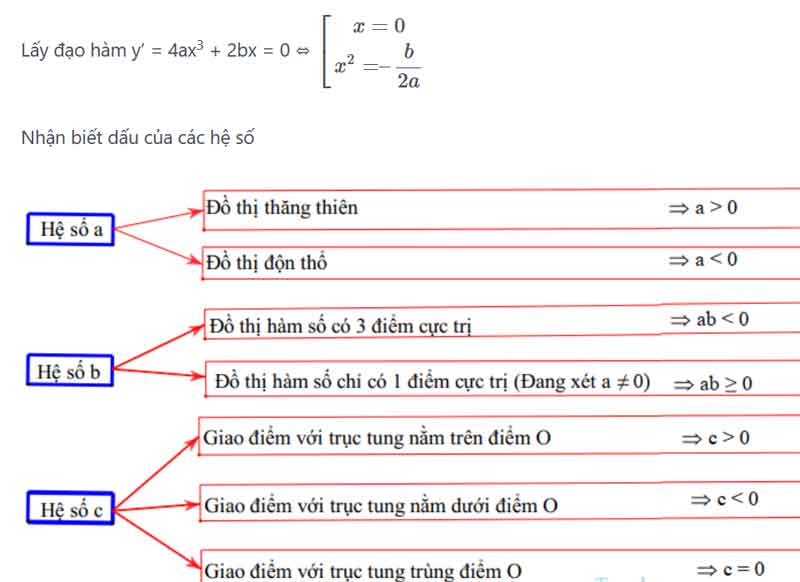
Với bài hàm số với các tham số là các giá trị cụ thể. Các tiêu chí để nhận dạng:

• Dựa vào tiệm cận đứng + tiệm cận ngang
• Dựa vào giao Ox,Oy
• Dựa vào sự đồng biến, nghịch biến

Với hàm số có chứa các tham số

Nhận biết dấu của 6 cặp tích số:

4 tích số này học sinh có thể ghi nhớ bằng cách hiểu bản chất của các yếu tố: Tiệm cận đứng, tiệm cận ngang, giao Ox, giao Oy, tính đồng biến, nghịch biến.

4. Đồ thị hàm số chứa dấu giá trị tuyệt đối

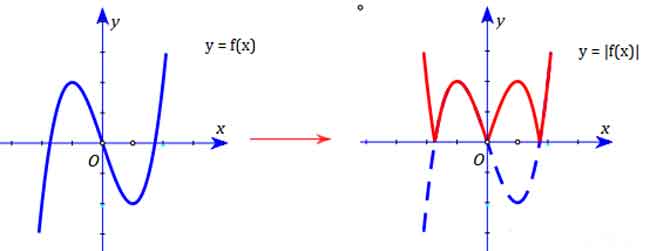
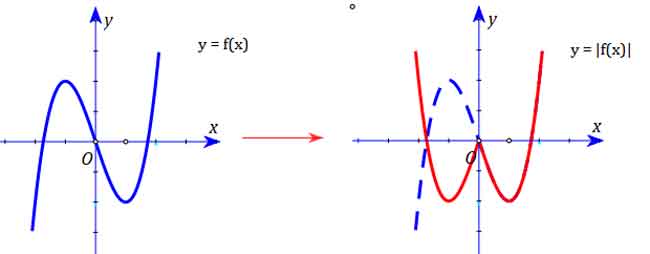
4.1 Từ đồ thị hàm số f(x) suy ra đồ thị hàm số |f(x)|

Thần chú: Trên giữ nguyên, dưới lấy đối xứng lên trên

Nghĩa là: Toàn bộ đồ thị nằm phía trên Ox của f(x) được giữ nguyên.

Toàn bộ đồ thị nằm phía dưới Ox của f(x) được lấy đối xứng lên trên.

4.2. Từ đồ thị hàm số f(x) suy ra đồ thị hàm số f(|x|)

Thần chú: Phải giữ nguyên, lấy đối xứng sang trái.

Nghĩa là: Toàn bộ đồ thị nằm phía bên phải Oy của f(x) được giữ nguyên, phần bên trái Oy của f(x) bỏ đi.

Lấy đối xứng phần bên phải sang trái.

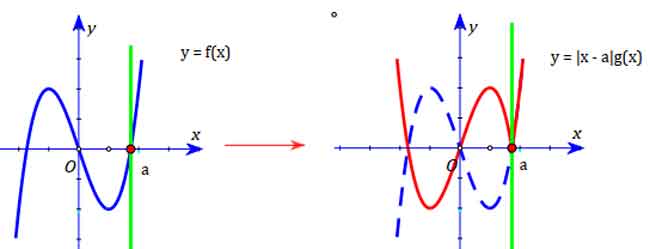
4.3. Từ đồ thị hàm số f(x) suy ra đồ thị hàm số |x – a|g(x) với (x – a)g(x) = f(x)

Thần chú: Phải a giữ nguyên, trái a lấy đối xứng qua Ox.

Nghĩa là: Toàn bộ đồ thị ứng với x > a của f(x) (Nằm phía bên phải đường thẳng x = a ) được giữ nguyên.

Toàn bộ đồ thị ứng với x < a của f(x) (Nằm phía bên trái đường thẳng x = a ) lấy đối xứng qua Ox.

5. Đồ thị hàm số f'(x)

– Số giao điểm với trục hoành => số lần đổi dấu của f'(x) => số điểm cực trị

– Nằm trên hay dưới trục hoành => f'(x) > 0 hoặc f'(x) < 0 trên 1 miền => Tính đơn điệu của hàm số.

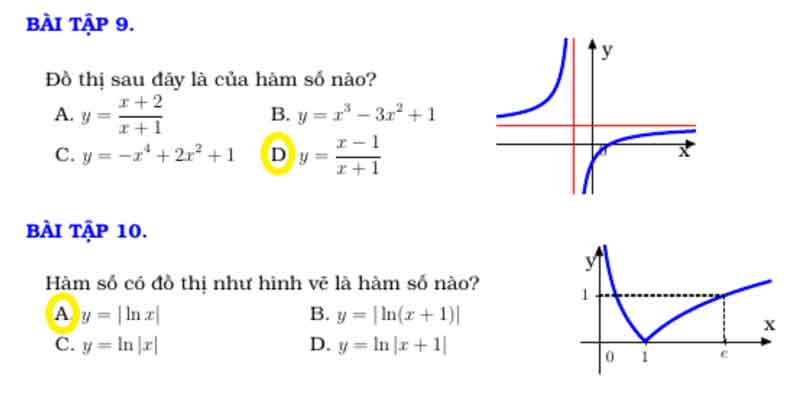
Cách nhận dạng đồ thị hàm số bậc 3

A. Phương pháp giải & Ví dụ

Các dạng đồ thị của hàm số bậc 3 y = ax3 + bx2 + cx + d (a ≠ 0)

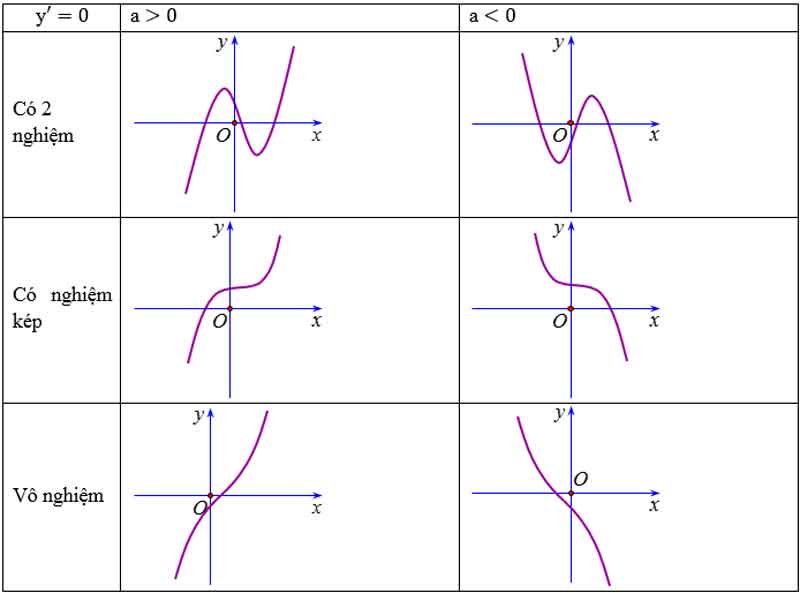
Đồ thị hàm số có 2 điểm cực trị nằm 2 phía so với trục Oy khi ac < 0

Đồ thị hàm số bậc ba luôn nhận điểm uốn làm tâm đối xứng

Ví dụ minh họa

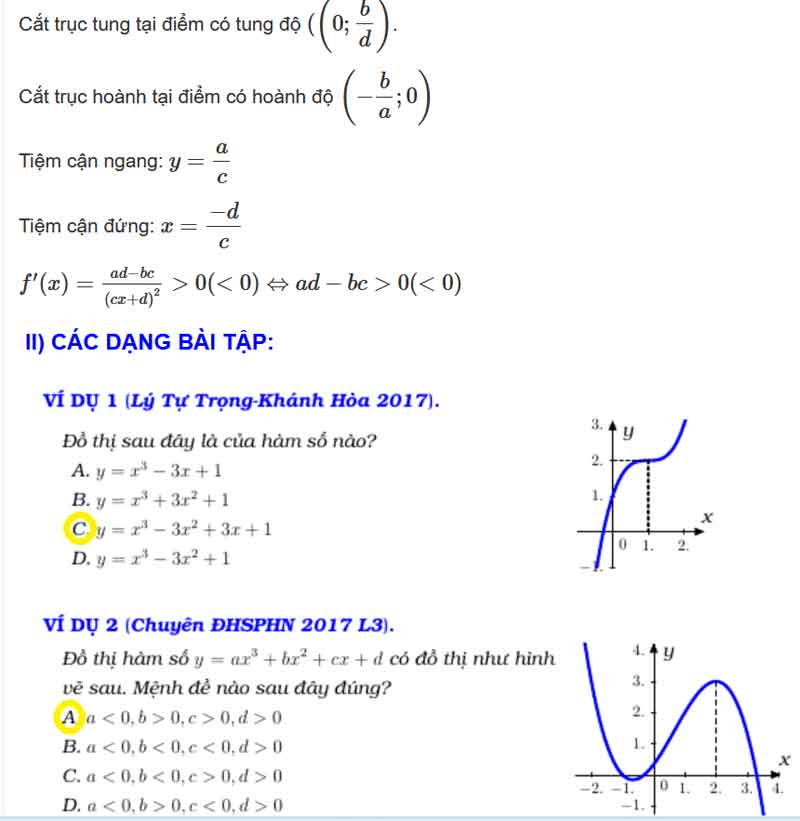
Ví dụ 1: Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x3 – 3x + 1.

B. y = -x3 + 3×2 + 1.

C. y = x3 – 3×2 + 3x + 1.

D. y = -x3 – 3×2 – 1.

Hướng dẫn

Nhìn dạng đồ thị thấy a > 0 , suy ra loại B, D.

Mặt khác hàm số không có cực trị nên loại A.

Chọn C.

Ví dụ 2: Cho hàm số bậc 3 có dạng: y = f(x) = ax3 + bx2 + cx + d.

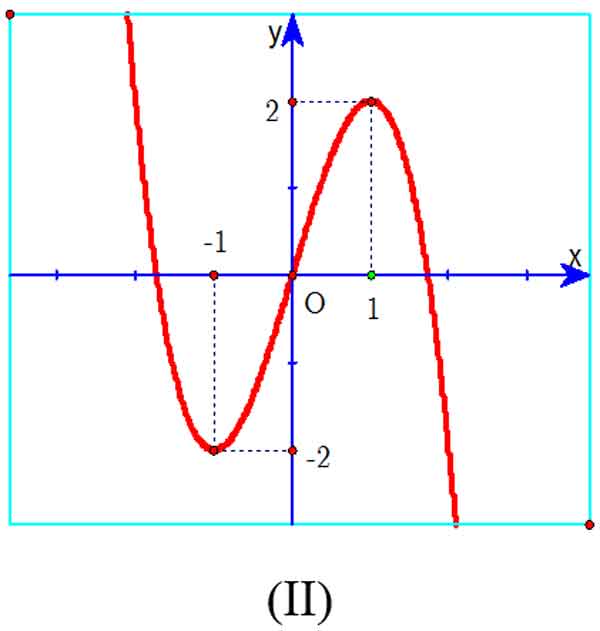
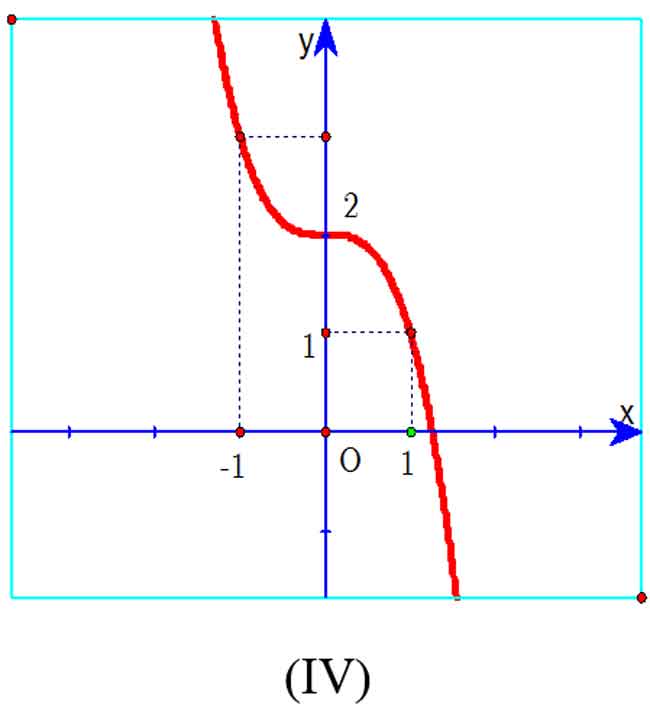
Hãy chọn đáp án đúng?

A. Đồ thị (IV) xảy ra khi a > 0 và f'(x) = 0 có nghiệm kép.

B. Đồ thị (II) xảy ra khi a ≠ 0 và f'(x) = 0 có hai nghiệm phân biệt.

C. Đồ thị (I) xảy ra khi a < 0 và f'(x) = 0 có hai nghiệm phân biệt.

D. Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm.

Hướng dẫn

Hàm số của đồ thị (II) có a < 0 nên điều kiện a ≠ 0 chưa đảm bảo. Do đó loại phương án B.

Hàm số của đồ thị (I) có a > 0 nên loại luôn phương án C.

Hàm số của đồ thị (IV) có a < 0 nên loại luôn phương án A.

Chọn D.

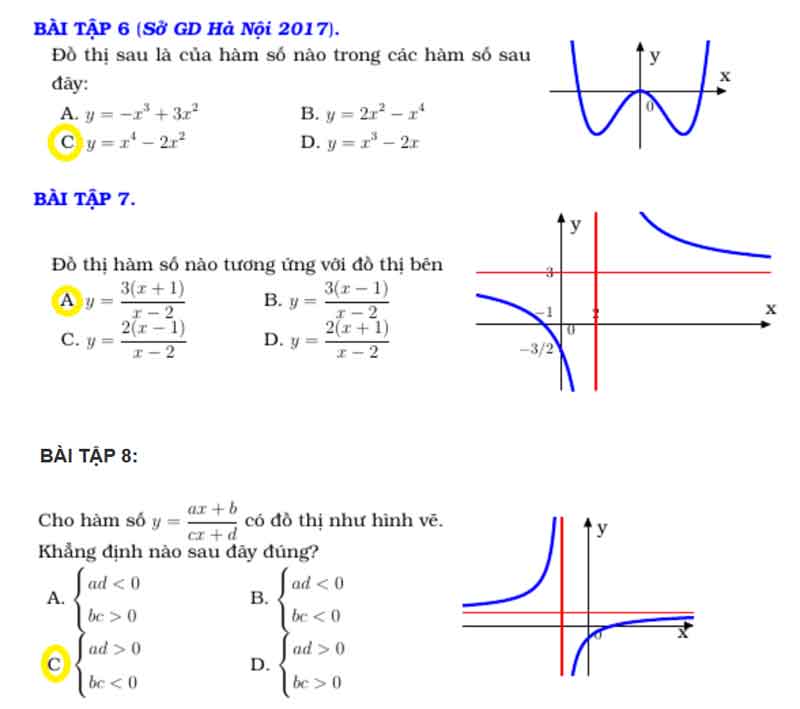
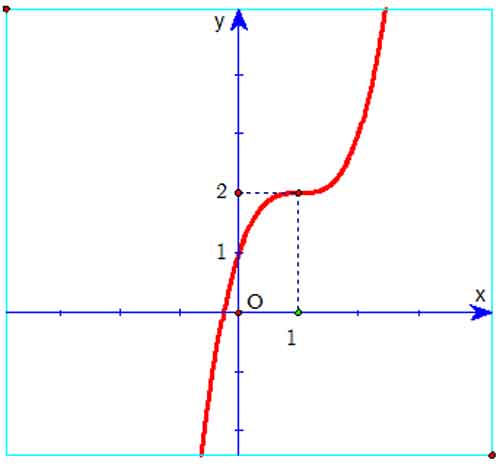
Ví dụ 3: Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên.

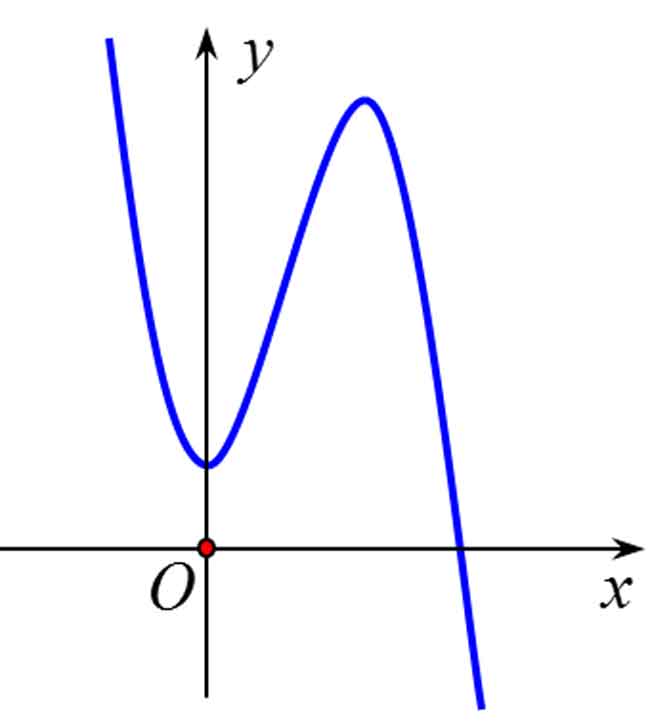
Mệnh đề nào dưới đây đúng?

A. a < 0,b > 0,c > 0,d > 0.

B. a < 0,b < 0,c = 0,d > 0.

C. a > 0,b < 0,c > 0,d > 0.

D. a < 0,b > 0,c = 0,d > 0.

Hướng dẫn

Từ hình dáng đồ thị ta suy ra hệ số a < 0,d > 0 loại đáp án C.

Ta có: y’ = 3ax2 + 2bx + c

Vì hàm số đạt cực tiểu tại điểm x = 0 nên y'(0) = 0 ⇒ c = 0 loại đáp án A.

Khi đó: y’ = 0 ⇔ 3ax2 + 2bx = 0 ⇔ x = 0 hoặc x = -2b/3a

Do hoành độ điểm cực đại dương nên -2b/3a > 0, mà a < 0 ⇒ b > 0.

Chọn D.

Cách nhận dạng đồ thị hàm số bậc 4

A. Phương pháp giải & Ví dụ

Các dạng đồ thị của hàm số bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0)

Đồ thị có 3 điểm cực trị :

Đồ thị có 1 điểm cực trị :

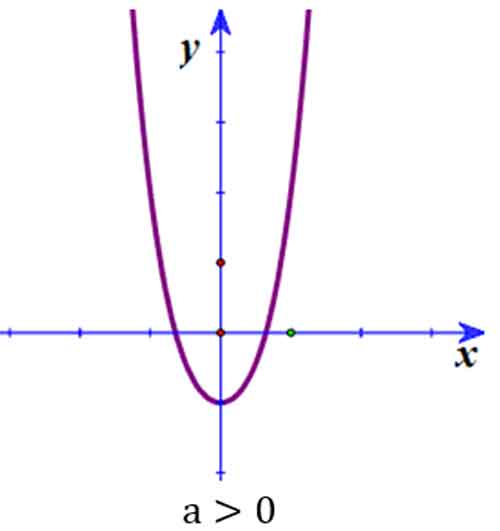
Đồ thị hàm bậc bốn trùng phương luôn nhận trục tung làm trục đối xứng

Ví dụ minh họa

Ví dụ 1: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

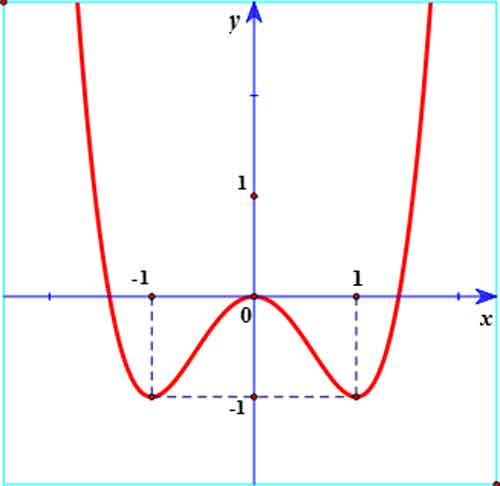
A. y = x4 – 3×2+1. B. y = x4 + 2×2.

C. y = x4 – 2×2. D. y = -x4 – 2×2.

Hướng dẫn

Từ đồ thị và đáp án suy ra đây là hàm số bậc 4 trùng phương: y = ax4 + bx2 + c (a ≠ 0) có 3 cực trị nên a > 0,b < 0. Do đó loại B, D. Do đồ thị qua O(0; 0)nên c = 0 loại A.

Từ đồ thị suy ra hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = ±1 nên loại A, B, D.

Chọn C.

Ví dụ 2: Giả sử hàm số y = ax4 + bx2 + c có đồ thị là hình bên dưới. Tìm a,b, c.

Hướng dẫn

y’ = 4ax3 + 2bx

Nhìn đồ thị ta thấy :

Ví dụ 3: Cho hàm số y=f(x) có đồ thị (C) như hình vẽ. Chọn khẳng định sai về hàm số f(x):

A. Hàm số f(x) tiếp xúc với Ox.

B. Hàm số f(x) đồng biến trên (-1; 0).

C. Hàm số f(x) nghịch biến trên (-∞; -1).

D. Đồ thị hàm số f(x) có tiệm cận ngang là y = 0.

Hướng dẫn

Từ đồ thị ta suy ra các tính chất của hàm số:

1. Hàm số đạt CĐ tại x = 0 và đạt CT tại x = ±1.

2. Hàm số tăng trên (-1; 0) và (1; +∞).

3. Hàm số giảm trên (-∞; -1) và (0; 1).

4. Hàm số không có tiệm cận.

Chọn D.

Cách nhận dạng đồ thị hàm số phân thức

A. Phương pháp giải & Ví dụ

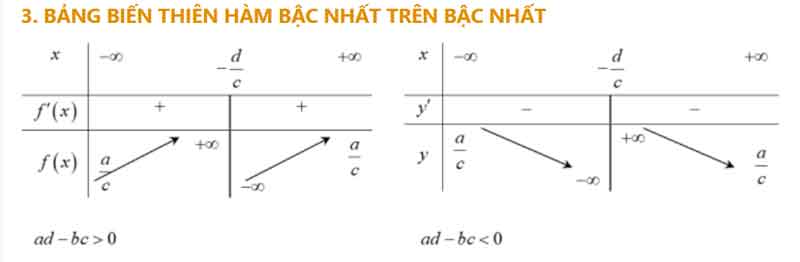
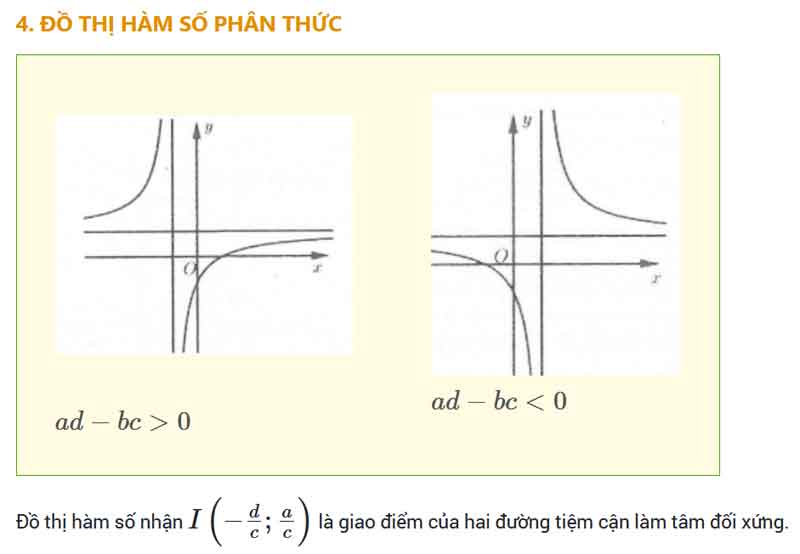
Các dạng đồ thị của hàm số nhất biến y = (ax + b)/(cx + d),(ab – bc ≠ 0)

Đồ thị hàm nhất biến luôn nhận giao của hai đường tiệm cận làm tâm đối xứng

Ví dụ minh họa

Ví dụ 1: Xác định a,b,c để hàm số y = (ax – 1)/(bx + c) có đồ thị như hình vẽ bên dưới.

Hướng dẫn

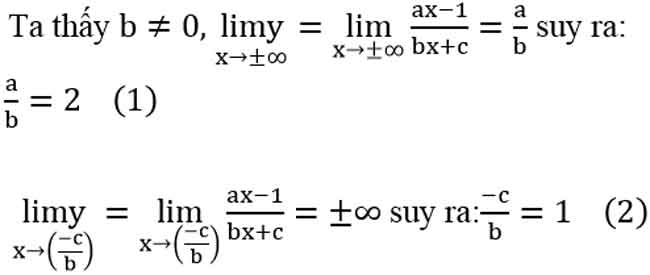
Đồ thị hàm số cắt Oy tại A(0; 1) nên (-1)/c = 1 ⇒ c = -1 (3)

Từ (1), (2), (3) ta có c = -1, b = 1, a = 2.

Ví dụ 2: Hàm số y = (x – 2)/(x – 1) có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.

a

b

c

Hướng dẫn

Hàm số y = (x – 2)/(x – 1) có tiệm cận đứng x = 1. Tiệm cận ngang y = 1 nên loại trường hợp D.

Đồ thị hàm số y = (x – 2)/(x – 1) đi qua điểm (0; 2) nên chọn đáp án A.

Ví dụ 3: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Hướng dẫn

Nhìn vào đồ thị ta thấy ngay tiệm cận đứng x = -1, tiệm cận ngang y = 2. Loại B, D.

Đồ thị hàm số đi qua điểm (0; -1).

y = (2x + 1)/(x + 1) khi x = 0 ⇒ y = 1. Loại đáp án B.

y = (2x – 1)/(x + 1) khi x = 0 ⇒ y = -1. Chọn đáp án A.

Bài tập vận dụng

Trong các câu hỏi dưới đây, hãy tìm hàm số có đồ thị tương ứng với đồ thị trong hình vẽ:

Bài 1:

A. y = -(1/3)x3 + 2×2 – 3x – 1/3

B. y = 1/3 x3 -3×2 + 4x – 1/3

C. y = x3 -6×2 + 9x – 1

D. y = 1/3×3 – 2×2 + 3x – 1/3

Hiển thị đáp án

Đáp án : D

Bài 2:

A. y = x3 – 3×2 + 3x + 1

B. y = x3 – 3×2 – 3x – 1

C. y = x3 – 3×2 + 3x – 1

D. y = -x3 + 3×2 – 3x – 1

Hiển thị đáp án

Đáp án : C

Bài 3:

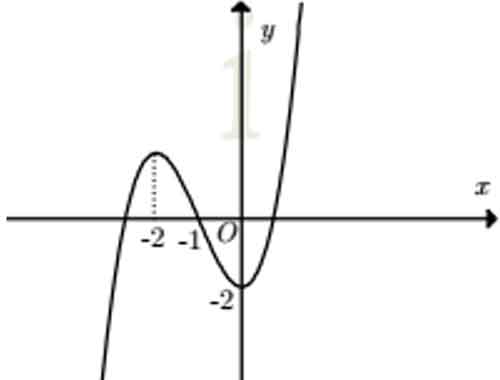
A. y = x3 + 3×2 – 2

B. y = x3 – 3×2 – 2

C. y = -x3 – 3×2 – 2

D. y = -x3 + 3×2 – 2

Hiển thị đáp án

Đáp án : A

Bài 4:

A. y = x3 – 2

B. y = x3 – 3x- 2

C. y = -x3 + 3x- 2

D. y = -x3 – 3x

Hiển thị đáp án

Đáp án : B

Bài 5:

A. y = -x3 + 3x

B. y = x3 – 3x

C. y = 2×3 – 6x

D. y=-2×3 + 6x

Hiển thị đáp án

Đáp án : C

Bài 6:

A. y = -x3 + 2

B. y = -x3 + 3x + 2

C. y = -x3 – x + 2

D. y = -x3 + 1

Hiển thị đáp án

Đáp án : A

Bài 7:

A. y = -x3 + 3x + 1

B. y = x3 – 3x + 1

C. y = -x3 + 3x + 2

D. y = x3 + 3x + 1

Hiển thị đáp án

Đáp án : B

Bài 8:

A. y = x3 – 3×2 – 1

B. y = -x3 + 3×2 – 1

C. y = -x3 + 6×2 – 1

D. y = -x3 + 3×2 – 4

Hiển thị đáp án

Đáp án : B

Bài 9:

A. y = -x3 – 3×2 + 2

B. y = -x3 + 3×2 + 4

C. y = x3 – 3×2 + 2

D. y = x3 – 3×2 + 4

Hiển thị đáp án

Đáp án : D

Bài 10:

A. y = (x + 1)2(2 – x)

B. y = (x + 1)2(1 + x)

C. y = (x + 1)2(2 + x)

D. y = (x + 1)2(1 – x)

Hiển thị đáp án

Đáp án : A

Bài 11:

A. y = -x3

B. y = x3 – 3x

C. y = x4 – 4×2

D. y = x3 – 3×2

Hiển thị đáp án

Đáp án : B

Bài 12:

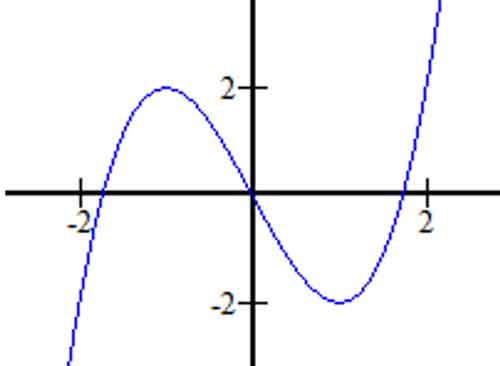
A. y = x3 – 3x

B. y = x3 – 3×2 + 3x – 1

C. y = -x3 + 3x

D. y = x3 + 3x

Hiển thị đáp án

Đáp án : A

Bài 13:

A. y = x3 – 3x+ 1

B. y = -x3 + 3x- 1

C. y = 2×3 – 6x+ 1

D. y = 2×3 – 3×2 + 1

Đáp án : A

Bài 14:

A. y = -x3 + 3x + 1

B. y = -2×3 + 1

C. y = -1/3 x3 + 2x + 1

D. y = 2×3 + 1

Hiển thị đáp án

Đáp án : B

Bài 15: Cho hàm số y = x3 + ax + b có đồ thị như hình bên. Chọn khẳng định đúng:

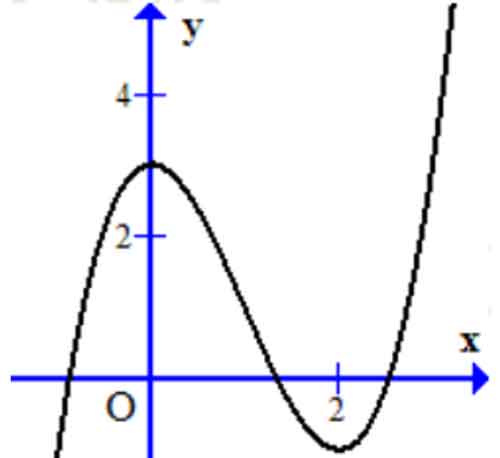
A. a < 0,b < 0

B. a > 0,b < 0

C. a > 0,b > 0

D. a < 0,b > 0

Hiển thị đáp án

Đáp án : D

Bài 16: Cho hàm số y = 1/3×3 + bx2 + cx + d có đồ thị như hình bên. Chọn khẳng định đúng:

A. b < 0,c > 0,d > 0

B. b < 0,c > 0,d < 0

C. b > 0,c > 0,d < 0

D. b < 0,c < 0,d < 0

Hiển thị đáp án

Đáp án : B

Bài 17: Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình bên. Chọn khẳng định đúng:

A. a < 0,b > 0,c > 0,d > 0

B. a < 0,b < 0,c < 0,d > 0

C. a < 0,b < 0,c > 0,d > 0

D. a < 0,b > 0,c < 0,d > 0

Hiển thị đáp án

Đáp án : A

Dấu hiệu nhận biết (dấu âm dương) các hệ số của hàm bậc ba dựa vào đồ thịĐồ thị thăng thiên ⇒ a > 0Đồ thị độn thổ ⇒ a < 0Điểm uốn “lệch phải” so với Oy hoặc 2 điểm cực trị lệch phải so với Oy ⇒ ab < 0Điểm uốn thuộc Oy, hai điểm cực trị cách đều trục Oy ⇒ b = 0Không có cực trị ⇒ c = 0 hoặc ac > 0Hai điểm cực trị nằm về hai phía trục tung Oy ⇒ ac < 0Có 1 điểm cực trị nằm trên Oy ⇒ c = 0Giao điểm với trục tung trùng điểm O ⇒ d = 0Giao điểm với trục tung nằm dưới điểm O ⇒ d < 0Giao điểm với trục tung nằm trên điểm O ⇒ d > 0Đồ thị hàm bậc 4 trùng phươngĐồ thị thăng thiên ⇒ a > 0Đồ thị độn thổ ⇒ a > 0Đồ thị hàm số có 3 điểm cực trị ⇒ ab < 0Đồ thị hàm số chỉ có 1 điểm cực trị (Đang xét a ≠ 0) ⇒ ab ≥ 0Giao điểm với trục tung nằm trên điểm O ⇒ c > 0Giao điểm với trục tung nằm dưới điểm O ⇒ c < 0Giao điểm với trục tung trùng điểm O ⇒ c = 0

Đồ thị hàm phân thức hữu tỉGiao Ox nằm phía “phải” điểm O ⇒ ab < 0Giao Ox nằm phía “trái” điểm O ⇒ ab > 0Không cắt Ox ⇒ a = 0Tiệm cận ngang nằm “phía trên” Ox ⇒ ac > 0Tiệm cận ngang nằm “phía dưới” Ox ⇒ ac < 0Tiệm cận ngang trùng Ox ⇒ a = 0Giao Oy nằm trên điểm O ⇒ bd > 0Giao Oy nằm dưới điểm O ⇒ bd < 0Giao Oy trùng gốc tọa độ O ⇒ b = 0Tiệm cận đứng nằm “bên phải” Oy ⇒ cd < 0Tiệm cận đứng nằm “bên trái” Oy ⇒ cd > 0Tiệm cận đứng trùng Oy ⇒ d = 0Đồ thị hàm số chứa dấu giá trị tuyệt đốiTừ đồ thị hàm số f(x) suy ra đồ thị hàm số |f(x)|: Toàn bộ đồ thị nằm phía trên Ox của f(x) được giữ nguyên. Toàn bộ đồ thị nằm phía dưới Ox của f(x) được lấy đối xứng lên trên.Từ đồ thị hàm số f(x) suy ra đồ thị hàm số f(|x|): Toàn bộ đồ thị nằm phía bên phải Oy của f(x) được giữ nguyên, phần bên trái Oy của f(x) bỏ đi, lấy đối xứng phần bên phải sang trái.Từ đồ thị hàm số f(x) suy ra đồ thị hàm số |x – a|g(x) với (x – a)g(x) = f(x): Toàn bộ đồ thị ứng với x > a của f(x) (Nằm phía bên phải đường thẳng x = a) được giữ nguyên, toàn bộ đồ thị ứng với x < a của f(x) (Nằm phía bên trái đường thẳng x = a) lấy đối xứng qua Ox.Đồ thị hàm số f'(x)Số giao điểm với trục hoành ⇒ số lần đổi dấu của f'(x) ⇒ số điểm cực trịNằm trên hay dưới trục hoành ⇒ f'(x) > 0 hoặc f'(x) < 0 trên 1 miền ⇒ Tính đơn điệu của hàm số

✅ Lớp 12 ⭐️⭐️⭐️⭐️⭐

🔢 GIA SƯ TOÁN 12