Trong chương trình môn Toán lớp 10, các em đã được học rất nhiều các dạng toán về đại số và hình học. Tuy nhiên, lượng bài tập trong sách giáo khoa không đủ để các em tự luyện ở nhà. Do đó, hôm nay Kiến Guru xin được giới thiệu các dạng bài tập toán 10 với đầy đủ và phong phú các dạng bài tập đại số và hình học. Trong đó, bài tập được phân loại thành các dạng cơ bản và nâng cao phù hợp với nhiều đối tượng học sinh : khá, giỏi, trung bình. Hy vọng, đây sẽ là nguồn tài liệu tự học hữu ích cho các em.
I. Các dạng bài tập toán 10 cơ bản
1. Bài tập toán lớp 10 đại số
Các bài tập toán 10 đại số xoay quanh 5 chương đã học trong sách giáo khoa gồm : mệnh đề – tập hợp, hàm số, pt và hpt, bđt và bpt, lượng giác.
Bài 1. Xác định tập hợp A ∩ B, A ∪ B, A B, CRAvới:
Bài 2. Cho tập hợp A = {x € R|3x + 2 ≤ 14} và B = [3m + 2; +∞). Tìm m để A∩B ≠Ø.
Bài 3. Tìm TXĐ hs sau:
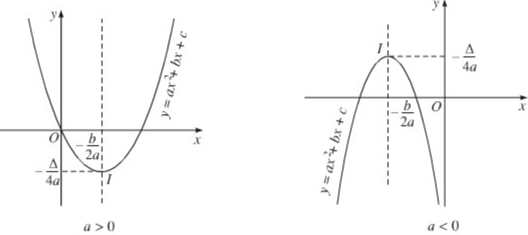
Bài 4. Lập BBT và vẽ đồ thị hs sau:
a. y = x2 – 4x + 3
b. y = -x2 +2x – 3
c. y = x2 + 2x
d. y = -2×2 -2
Bài 5. Tìm Parabol y = ax2 – 4x + c, biết rằng Parabol :
- Đi qua hai điểm A(1; -2) và B(2; 3).
- Có đỉnh I(-2; -2).
- Có hoành độ đỉnh là -3 và đi qua điểm P(-2; 1).
- Có trục đối xứng là đường thẳng x = 2 và cắt trục hoành tại điểm (3; 0).
Bài 6. Giải các phương trình sau:
Bài 7. Biết X1, X2 là nghiệm của phương trình 5×2 – 7x + 1 = 0. Hãy lập phương trình bậc hai có các nghiệm
Bài 8.
Bài 9. Tìm điều kiện của bất phương trình:
Bài 10. Xét dấu f(x) = x2 – 4x -12
Bài 11. Giải các bất phương trình sau:
Bài 12. Giải các bất phương trình sau
Bài 13. Tìm m để x2 + 2(m-1)x + m + 5 > 0, ∀x€R
Bài 14.
Đăng Ký Học Ngay: Toán thầy Mạnh Lớp 10
II. Bài tập toán lớp 10 hình học
Các bài tập toán 10 hình học bao gồm kiến thức của 3 chương: vectơ, tích vô hướng của 2 vectơ và ứng dụng, mặt phẳng tọa độ Oxy.
Bài 1. Gọi I, J lần lượt là trung điểm các cạnh AB, CD của tứ giác ABCD. Gọi G là trung điểm của đoạn thẳng IJ.
Bài 2.
Bài 3.
Cho tam giác ABC với J là trung điểm của AB, I là trung điểm của JC. M, N là hai điểm thay đổi trên mặt phẳng sao cho
Chứng minh M, N, I thẳng hàng.
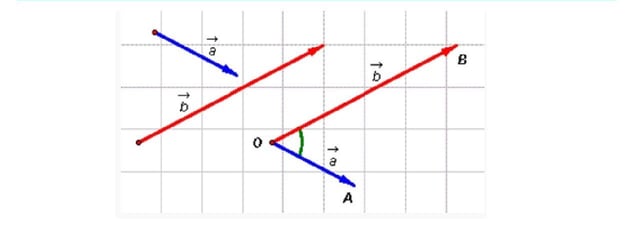
Bài 4. Cho a = (3;2), b = (4;-5), c = (-6;1)
a. Tính tọa độ của u = 3a + 2b -4c
b. Tính tọa độ của x sao cho x + a = b – c
c. Phân tích vectơ c theo hai vectơ a và b.
Bài 5. Trong mặt phẳng tọa độ Oxy, cho A(-5 ; -2) , B(-5 ; 3) , C(3 ; 3)
- Tính tọa độ 3 vectơ
- Tìm tọa độ I của đoạn thẳng BC và tọa độ trọng tâm G của tam giác ABC.
- c) Tìm tọa D để tứ giác ABCD là hình bình hành.
Bài 6. Cho tam giác ABC có A(-1;1); B(1;3); C(1;-1).
- Tìm chu vi của tam giác ABC.
- Chứng minh tam giác ABC vuông cân. Từ đó suy ra diện tích của tam giác ABC.
Bài 7. Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A(0;2), B(-2;0), C(-2;2).
- Tính tích vô hướng . Từ đó suy ra hình dạng của tam giác ABC.
- Tìm tọa D sao cho tứ giác ACBD là hình bình hành.
Bài 8. Cho ba điểm A(-1; 1), B(5; -2), C(2; 7).
- CMR : 3 điểm A, B, C lập thành 3 đỉnh của một tam giác.
- Tìm tọa độ I sao cho .
- Tìm tọa độ trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC.
- Tính chu vi tam giác ABC.
- Tính cosin các góc của tam giác ABC.
Bài 9. Cho A(1,-1); B(-2,5)
a. Viết phương trình tổng quát đường thẳng đi qua A và B.
b. Tìm góc giữa và đường thẳng d: x – y + 3 = 0.
Bài 10. CMR trong một tam giác ABC
a/ a = b.cosC + c.cosB
b/ sinA = sinB.cosC + sinC.cosB
II. Các dạng bài tập toán 10 nâng cao
Trong phần này, chúng tôi sẽ giới thiệu các dạng bài tập toán 10 nâng cao. Đây là các bài tập liên quan đến phương trình, bpt, bất đẳng thức và tọa độ mặt phẳng.
Đặc biệt, vì đây là các bài toán khó mà đa số các bạn học sinh không làm được nên các bài tập mà chúng tôi chọn lọc đều là các bài tập toán 10 nâng cao có đáp án để các em dễ dàng tham khảo cách giải những dạng toán này
Câu 1:
Đáp án
Ta có:
Câu 2: Giải Bất phương trình :
Ta có:bai-tap-toan-10
Câu 3:
Cho phương trình : mx2 + 2(m-2)x + m – 3 = 0 (1)
a/ Giải và biện luận phương trình (1) theo m.
b/ Tìm m để phương trình (1) có hai nghiệm x1, x2 sao cho :
.
* Khi m = 0 thì (1) trở thành : .
* Khi m ≠ 0 thì (1) là phương trình bậc hai có Δ = 4 – m.
+ Nếu m > 4 thì phương trình (1) vô nghiệm.
+ Nếu m ≤ 4 thì pt (1) có 2 nghiệm : 
.
Kết luận :
+ m = 0 : .
+ m > 4 : S = Ø
+ m ≤ 4 và m ≠ 0: Phương trình (1) có hai nghiệm : .
* Khi m ≤ 4 và m ≠ 0 thì phương trình (1) có hai nghiệm x1, x2.
*
* Thay vào và tính được : thoả mãn điều kiện m ≤ 4 và m ≠ 0 .
Câu 4:
Trong Oxy cho ΔABC với A(1;-2), B(5;-2),C(3;2). Tìm toạ độ trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp I của ΔABC.
Đáp án :
Toạ độ trọng tâm G :.
Toạ độ trực tâm H :
* .
* H (3 ; – 1 ).
Toạ độ tâm đường trong ngoại tiếp I :
Câu 5: Chứng minh rằng nếu x,y,z là số dương thì .
Trong các dạng bài tập toán 10 thì bất đẳng thức lúc nào cũng là dạng bài tập khó nhất, đòi hỏi các em khả năng tư duy và biến đổi thành thạo. Tuy nhiên, trong tát cả các dạng toán về bất đẳng thức thì đa số các bài tập đều liên quan đến bất đẳng thức cosi nên các em hãy học kĩ về bất đẳng thức cosi và các bài tập liên quan đến nó.
Câu 6: Tìm giá trị lớn nhất của hàm số y=(-2x+3)(x-1), với
Ta c ó y=(-2x+3)(x-1)=½(-2x+3)(2x-2),
Với 
. Ta có 2x-2>0 và -2x+3>0.
Áp dụng bất đẳng thức côsi cho 2 số dương là 2x-2>0 và -2x+3>0. ta được:
Câu 7:
Cho A(-4;2);B(2;6);C(0;-2)
a).Hãy tìm toạ độ điểm D sao cho tứ giác ABCD là hình bình hành
b) Xác định toạ độ trọng tâm G của tam giác ABC
c) Xác định toạ độ trực tâm H của tam giác ABC
Giải
a) Tứ giác ABCD là hình bình hành nên (1)
Vậy D(-6;-2) 0,25
b) Gọi G là trọng tâm của tam giác.Khi đó
c) Gọi H là trực tâm của tam giác ABC. Khi đó:
Ta có
Kiến Guru vừa giới thiệu xong các dạng bài tập toán 10 cơ bản và nâng cao. Tài liệu được biên soạn với mục đích giúp cho các em học sinh lớp 10 rèn luyện kĩ năng giải bài tập, ôn lại những kiến thức từ những bài tập cơ bản đến nâng cao trình độ ở các bài tập nâng cao. Hy vọng, các em học sinh sẽ chăm chỉ giải hết các dạng bài tập trong bài và theo dõi những bài viết tiếp theo của Kiến Guru về những chuyên đề toán khác. Chúc các em học tập tốt và đạt điểm tốt trong những bài kiểm tra trong năm học lớp 10 này.
Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!