Trong toán học, định lý Pytago là một liên hệ căn bản trong hình học giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại. Đây là một lí thuyết quan trọng trong hình học nói riêng cũng như trong toán học nói chung. Loạt bài viết này sẽ chia sẽ kĩ thuật sử dụng Solve trên máy tính Casio fx-580VNX để giải phương trình Pythagoras nhanh chóng và chính xác hơn.
Ví dụ 1.
Giải phương trình ${{A}^{2}}+{{B}^{2}}={{C}^{2}}$ trong các trường hợp sau a. Cho $A=4,C=5$. Tìm $B$. b. Cho $B=6,C=10$. Tìm $A$.
Hướng dẫn
a. Nhập vào phương trình
$${{A}^{2}}+{{B}^{2}}={{C}^{2}}$$
Qz(A)d+Qx(B)dQrQu(C)d
Nhập vào các tham số. Lưu ý nghiệm cần tìm là $B$.
qr4=R5=E=
b. Tiếp tục nhập vào các tham số. Lưu nghiệm đang cần tìm là $A$
CqrR6=10=EE=
Lưu ý. Trên máy tính Casio fx-580VN X, khi nhập 1 phương trình có nhiều biến nhớ, lúc thao tác Solve bạn để con trỏ ở biến nhớ nào, máy tính Casio fx-580VN X sẽ tự động hiểu biến nhớ đó là ẩn và các biến nhớ khác là hằng số. Lệnh Solve sẽ giải phương trình dựa trên ẩn đó, giá trị bạn gán vào ẩn sẽ là giá trị ban đầu mà bạn nhập vào. Ví dụ như khi bạn nhập vào ví dụ 1 câu a với $A=4,C=5 $ thì máy tính sẽ hiểu là
$$ 4^2+x^2=5^2 $$
Và máy Fx580VN X sẽ bắt đầu Solve tại $x=0$
Các bạn có thể tìm hiểu thêm tại đường link dưới đây:
Bài tập 1.
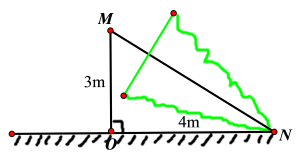
Một cái cây bị gió bão quật gãy như hình vẽ. Biết chiều cao từ gốc cây đến chỗ bị gãy là $3$ mét, khoảng cách từ gốc đến phần ngọn đổ xuống đất là $4 $ mét. Hãy tính chiều cao của cây đó lúc trước khi gãy?
Hướng dẫn
Áp dụng định lý Pi-ta-go trong tam giác vuông $OMN$, ta được:
$M{{N}^{2}}=O{{M}^{2}}+O{{N}^{2}}={{3}^{2}}+{{4}^{2}}=25 Rightarrow MN=sqrt{25}=5$

Vậy chiều cao cây lúc chưa gãy là : $3+5=8left( m right)$
Bài tập 2
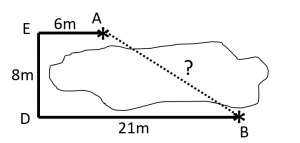
Để tính khoảng cách từ 2 điểm $A,B$ ở hai bên bờ ao (như hình vẽ), An đã đi theo ven bờ đê theo đường $Ato Eto Dto B$, với ước lượng bước chân An tính được $AE=6m,ED=8m,DB=21m$. (Giả sử $AEbot DE;DEbot DB$). Em hãy tính xem An tính được khoảng cách $AB$ dài bao nhiêu mét?
Hướng dẫn
Theo đề bài ta có hình vẽ
Vẽ $AKbot BD$ ($K$ thuộc $BD$)
Theo hình vẽ $left{ begin{aligned}& AK=DE=8m \ & Atext{E}=DK=6m \ end{aligned} right.$
Từ đó $Rightarrow BK=BD-DK=21-6=15left( m right)$
Áp dụng định lý pitago trong $Delta ABK $ vuông tại $ K$

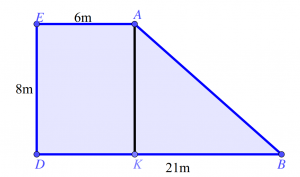
begin{align*}&AB^2= AK^2 + BK^2\&Rightarrow AB^2 = 8^2 + 15^2=289\&Rightarrow AB = 17 end{align*} Vậy khoảng cách $AB$ là $ 17m $.
Bài tập 3
Trong lúc bạn Nam dựng tủ cho đứng thẳng, tủ có bị vướng vào trần nhà cao $21 dm$ không ?

Hướng dẫn
Gọi $ ABCD $ là một mặt của tủ. $ ABCD $ là hình chữ nhật vì tủ là hình hộp chữ nhật.
Khi dựng tủ, chân tủ đứng yên tại $ A $. Muốn biết tủ có bị vướng trần nhà hay không ta chỉ cần so sánh đoạn $ AC $ với $ 21 dm $ là chiều cao của bức tường.
Tam giác $ ABC $ vuông tại $ B $ với
$$ AB=4 dm, BC=20 dm $$
Theo định lí Pythagoas, ta có:
begin{equation}AC^2=AB^2+BC^2=4^2+20^2=416end{equation}
Ta lại có $ 21^2=441Rightarrow AB<21 $.
Vậy lúc dựng tủ đứng thẳng thì tủ không vướng trần nhà.
——————————————-
Trên đây là một số bài tập về phương trình Pythagoras nhằm giúp các em hiểu rõ hơn về tính năng của máy tính Casio fx-580VN X và tính toán các bài toán nhiều ẩn số một cách chính xác hơn. Bài viết khó tránh khỏi thiếu sót, các bạn có đóng góp gì thì cmt hoặc gửi tin nhắn qua fanpage nhé. Trân trọng.




