Các phương pháp chứng minh 2 đoạn thẳng bằng nhau từ đơn giản đến phức tạp1. Cách chứng minh theo kiến thức Lớp 6, 7* Phương pháp 1: Dựa vào số đo của các đoạn thẳng=> Cách làm:- Đưa về bài toán chứng minh hai đoạn thẳng có cùng số đo- Khi trên hình có đoạn thẳng thứ ba bằng hai đoạn còn lại: Đưa về bài toán chứng minh hai đoạn thẳng cùng bằng một đoạn thẳng thứ ba.- Khi bài toán đã cho một điểm nằm giữa hai điểm còn lại: Đưa về bài toán chứng minh hai đoạn thẳng đó bằng tổng/ hiệu của hai đoạn thẳng bằng nhau từng đôi một.* Phương pháp 2: Đưa về bài toán chứng minh hai đoạn thẳng đó là hai cạnh tương ứng của hai tam giác bằng nhau.* Phương pháp 3: Vận dụng các tính chất của tam giác cân, tam giác đều=> Cách làm: Đưa về bài toán chứng minh hai đoạn thẳng đó là cạnh bên của các tam giác (tam giác cân hoặc tam giác đều).* Phương pháp 4: Đưa về bài toán chứng minh hai đoạn thẳng tạo bởi trung điểm của đoạn cho trước.
2. Cách chứng minh theo kiến thức Lớp 8* Phương pháp 1: Áp dụng Định lí Ta-lét – Tam giác đồng dạng* Phương pháp 2: Vận dụng tính chất của đường trung bình trong tam giác; tính chất đường trung tuyến trong tam giác vuông.* Phương pháp 3: Vận dụng tính chất về cạnh và đường chéo của các tứ giác đặc biệt:- Hai đường chéo của hình vuông, hình thang cân, hình chữ nhật- Hai cạnh đối của hình thoi, hình vuông, hình chữ nhật, hình bình hành=> Cách làm: Đưa về bài toán chứng minh hai đoạn thẳng đó là các đường chéo của hình vuông, thang cân hay hình chữ nhật; cạnh đối của hình thoi, hình bình hành, hình chữ nhật,…3. Cách chứng minh theo kiến thức lớp 9Phương pháp: Vận dụng các định lí- Hai dây cách đều tâm của một đường tròn- Dây cung và khoảng cách đến tâm:+ Trong một đường tròn: Hai dây bằng nhau thì cách đều tâm. Hai dây cách đều tâm thì bằng nhau.+ Trong hai dây của một đường tròn: Dây nào lớn hơn thì dây đó gần tâm hơn. Dây nào gần tâm hơn thì dây đó lớn hơn.- Đường nối tâm của hai đường tròn cắt nhau.- Hai tiếp tuyến cùng xuất phát từ một điểm đến một đường tròn.
Một số ví dụ cụ thể cho bài toán chứng minh 2 đoạn thẳng bằng nhauBài tập 1: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt cạnh AC tại điểm D. Trên cạnh BC, lấy điểm E sao cho: BE = AB. Chứng minh rằng: AD = DE.Hướng dẫn giải: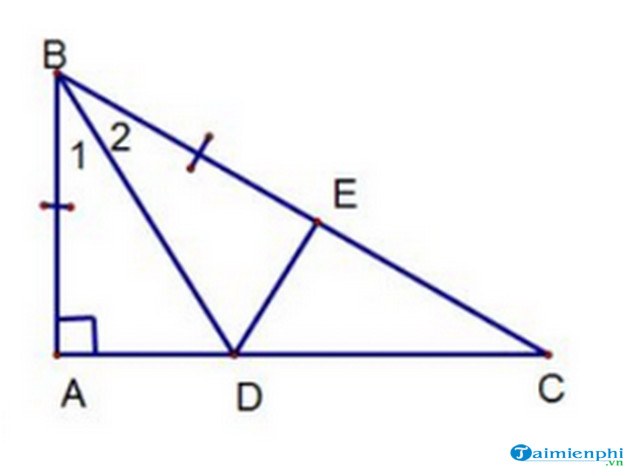
Xét tam giác ABD và tam giác EBD, có:BD là cạnh chungBE = AB (đề bài đã cho)góc ABD = góc DBE (vì BD là tia phân giác của góc B)=> Tam giác ABD = tam giác EBD (c.g.c)=> AD = DE (điều phải chứng minh).Bài tập 2: Cho tam giác ABC, điểm M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm N sao cho MN = MA. Hãy chứng minh:a) AC = BNb) AB = NCHướng dẫn giải:
a) Chứng minh: AC = BNXét tam giác ACM và tam giác NBM, có:MB = MC (M là trung điểm của BC)góc AMC = góc NMB (vì đối đỉnh)MA = MN (đề bài đã cho)=> Tam giác ACM = tam giác NBM (c.g.c)=> AC = BN (điều phải chứng minh).b) Chứng minh: AB = NCXét tam giác ABM và tam giác NCM, có:MB = MC (M là trung điểm của BC)góc AMB = góc NMC (đối đỉnh)MA = MN (đề bài đã cho)=> Tam giác ABM = tam giác NCM (c.g.c)=> AB = NC (điều phải chứng minh).
Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!