1) PHƯƠNG PHÁP HỆ SỐ HÓA BIẾN
- Bước 1 : Dựa vào hệ thức điều kiện buộc của đề bài chọn giá trị thích hợp cho biến
- Bước 2 : Tính các giá trị liên quan đến biến rồi gắn vào A, B, C nếu các giá trị tính được lẻ
- Bước 3 : Quan sát 4 đáp án và chọn đáp án chính xác
2) VÍ DỤ MINH HỌA VD1-[Đề minh họa THPT Quốc gia 2017] Đặt $a = {log _2}3,,,b = {log _5}3.$Hãy biểu diễn ${log _6}45$ theo a và b A. ${log _6}45 = frac{{a + 2ab}}{{ab}}$ B. ${log _6}45 = frac{{2{a^2} – 2ab}}{{ab}}$ C. ${log _6}45 = frac{{a + 2ab}}{{ab + b}}$ D. ${log _6}45 = frac{{2{a^2} – 2ab}}{{ab + b}}$
GIẢI
Tính giá trị của $a = {log _2}3$. Vì giá trị của a ra một số lẻ vậy ta lưu a vào A Tính giá trị của $b = {log _5}3$ và lưu vào B Bắt đầu ta kiểm tra tính đúng sai của đáp án A. Nếu đáp án A đúng thì hiệu ${log _6}45 – frac{{a + 2ab}}{{ab}}$ phải bằng 0. Ta nhập hiệu trên vào máy tính Casio và bấm nút = 
Kết quả hiển thị của máy tính Casio là 1 giá trị khác 0 vậy đáp án A sai Tương tự như vậy ta kiểm tra lần lượt từng đáp án và ta thấy hiệu ${log _6}45 – frac{{a + 2ab}}{{ab + b}}$ bằng 0 
Vậy ${log _6}45 = frac{{a + 2ab}}{{ab + b}}$hay đáp số C là đúng Cách tham khảo : Tự luận Ta có $a = {log _2}3 = frac{1}{{{{log }_3}2}} Rightarrow {log _3}2 = frac{1}{a}$ và ${log _3}5 = frac{1}{b}$ Vậy ${log _6}45 = frac{{{{log }_3}45}}{{{{log }_3}6}} = frac{{{{log }_3}left( {{3^2}.5} right)}}{{{{log }_3}left( {3.2} right)}} = frac{{2 + {{log }_3}5}}{{1 + {{log }_3}2}} = frac{{2 + frac{1}{b}}}{{1 + frac{1}{a}}} = frac{{a + 2ab}}{{ab + b}}$ Bình luận
- Cách tự luận trong dạng bài này chủ yếu để kiểm tra công thức đổi cơ số : công thức 1 : ${log _a}x = frac{1}{{{{log }_x}a}}$ (với $a ne 1$) và công thức 2 : ${log _a}x = frac{{{{log }_b}x}}{{{{log }_a}x}}$ (với $b > 0;b ne 1$)
- Cách Casio có vẻ nhiều thao tác nhưng dễ thực hiện và độ chính xác 100%. Nếu tự tin cao thì làm tự luận, nếu tự tin thấp thì nên làm Casio vì làm tự luận mà biến đổi sai 1 lần thôi rồi làm lại thì thời gian còn tốn hơn cả làm theo Casio
VD2-[THPT Yên Thế – Bắc Giang 2017] Cho ${9^x} + {9^{ – x}} = 23$. Khi đó biểu thức $P = frac{{5 + {3^x} + {3^{ – x}}}}{{1 – {3^x} – {3^{ – x}}}}$ có giá trị bằng? A. 2 B. $frac{3}{2}$ C. $frac{1}{2}$ D. $ – frac{5}{2}$
GIẢI
Từ phương trình điều kiện ${9^x} + {9^{ – x}} = 23$ ta có thể dò được nghiệm bằng chức năng SHIFT SOLVE Lưu nghiệm này vào giá trị A Để tính giá trị biểu thức P ta chỉ cần gắn giá trị x=A sẽ được giá trị của P 
Vậy rõ ràng D là đáp số chính xác Cách tham khảo : Tự luận Đặt $t = {3^x} + {3^{ – x}} Leftrightarrow {t^2} = {9^x} + {9^{ – x}} + 2 = 25 Leftrightarrow t = pm 5$ Vì ${3^x} + {3^{ – x}} > 0$ vậy t>0 hay 5 Với ${3^x} + {3^{ – x}} = 5$ . Thế vào P ta được $P = frac{{5 + 5}}{{1 – 5}} = – frac{5}{2}$ Bình luận
- Một bài toán hay thể hiện sức mạnh của Casio
- Nếu trong một phương trình có cụm ${a^x} + {a^{ – x}}$ thì ta đặt ẩn phụ là cụm này, khi đó ta có thể biểu diễn ${a^{2x}} + {a^{ – 2x}} = {t^2} – 2$ và ${a^{3x}} – {a^{ – 3x}} = {t^3} – 3t$
VD3-[Chuyên Khoa Học Tự Nhiên 2017] Cho ${log _9}x = {log _{12}}y = {log _{16}}left( {x + y} right)$ Giá trị của tỉ số $frac{x}{y}$ là ? A. $frac{{ – 1 – sqrt 5 }}{2}$ B. $frac{{sqrt 5 – 1}}{2}$ C. 1 D. 2
GIẢI
Từ đẳng thức ${log _9}x = {log _{12}}y$$ Rightarrow y = {12^{{{log }_9}x}}$ . Thay vào hệ thức ${log _9}x = {log _{16}}left( {x + y} right)$ ta được : ${log _9}x – {log _{16}}left( {x + {{12}^{{{log }_9}x}}} right) = 0$ Ta có thể dò được nghiệm phương trình ${log _9}x – {log _{16}}left( {x + {{12}^{{{log }_9}x}}} right) = 0$ bằng chức năng SHIFT SOLVE 
Lưu nghiệm này vào giá trị A Ta đã tính được giá trị x vậy dễ dàng tính được giá trị $y = {12^{{{log }_9}x}}$ . Lưu giá trị y này vào biến B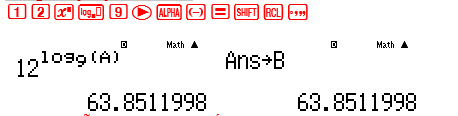 
Tới đây ta dễ dàng tính được tỉ số $frac{x}{y} = frac{A}{B}$ 
Đây chính là giá trị $frac{{sqrt 5 – 1}}{2}$ và đáp số chính xác là B Cách tham khảo : Tự luận Đặt ${log _9}x = {log _{12}}y = {log _{16}}left( {x + y} right) = t$ vậy $x = {9^t};y = {12^t};x + y = {16^t}$
- Ta thiết lập phương trình $frac{x}{y} = frac{{{3^x}}}{{{4^x}}} = {left( {frac{3}{4}} right)^x}$ và $frac{x}{y} + 1 = frac{{x + y}}{y} = frac{{{{16}^x}}}{{{{12}^x}}} = {left( {frac{4}{3}} right)^x}$
- Vậy $frac{x}{y}left( {frac{x}{y} + 1} right) = 1 Leftrightarrow {left( {frac{x}{y}} right)^2} + frac{x}{y} – 1 = 0 Leftrightarrow frac{x}{y} = frac{{ – 1 pm sqrt 5 }}{y}$ Vì $frac{x}{y} > 0$ nên $frac{x}{y} = frac{{ – 1 + sqrt 5 }}{2}$
Bình luận • Một bài toán cực khó nếu tính theo tự luận • Nhưng nếu xử lý bằng Casio thì cũng tương đối dễ dàng và độ chính xác là 100%
VD4-[THPT Nguyễn Trãi – HN 2017] Cho$K = {left( {{x^{frac{1}{2}}} – {y^{frac{1}{2}}}} right)^2}{left( {1 – 2sqrt {frac{y}{x}} + frac{y}{x}} right)^{ – 1}}$ với x>0; y>0). Biểu thức rút gọn của K là ? A. x B. 2x C. x+1 D. x-1
GIẢI
Ta hiểu nếu đáp án A đúng thì K=x hay hiệu ${left( {{x^{frac{1}{2}}} – {y^{frac{1}{2}}}} right)^2}{left( {1 – 2sqrt {frac{y}{x}} + frac{y}{x}} right)^{ – 1}} – x$ bằng 0 với mọi giá trị x;y thỏa mãn điều kiện x>0; y>0 Nhập hiệu trên vào máy tính Casio 
Chọn 1 giá trị X=1.25 và Y=3 bất kì thỏa x>0; y>0 rồi dùng lệnh gán giá trị CALC Ta đã tính được giá trị x vậy dễ dàng tính được giá trị $y = {12^{{{log }_9}x}}$ Vậy ta khẳng định 90% đáp án A đúng Để cho yên tâm ta thử chọn giá trị khác, ví dụ như X=0.55Y= 1.12 Kết quả vẫn ra là 0 , vậy ta chắc chắn A là đáp số chính xác Cách tham khảo : Tự luận Rút gọn ${left( {{x^{frac{1}{2}}} – {y^{frac{1}{2}}}} right)^2} = {left( {sqrt x – sqrt y } right)^2}$ Rút gọn ${left( {1 – 2sqrt {frac{y}{x}} + frac{y}{x}} right)^{ – 1}} = {left[ {{{left( {sqrt {frac{y}{x}} – 1} right)}^2}} right]^{ – 1}} = {left( {frac{{sqrt y – sqrt x }}{{sqrt x }}} right)^{ – 2}} = {left( {frac{{sqrt x }}{{sqrt y – sqrt x }}} right)^2}$ Vậy $K = {left( {sqrt x – sqrt y } right)^2}{left( {frac{{sqrt x }}{{sqrt y – sqrt x }}} right)^2} = x$ Bình luận • Chúng ta cần nhớ nếu 1 khẳng định ( 1 hệ thức đúng ) thì nó sẽ đúng với mọi giá trị x,y thỏa mãn điều kiện đề bài . Vậy ta chỉ cần chọn các giá trị X,Y>0 để thử và ưu tiên các giá trị này hơi lẻ, tránh số tránh (có khả năng xảy ra trường hợp đặc biệt)
VD5-[Thi thử Báo Toán Học Tuổi Trẻ 2017] Cho hàm số $fleft( x right) = {2^{{x^2} + 1}}$ Tính giá trị của biểu thức $T = {2^{ – {x^2} – 1}}.f’left( x right) – 2xln 2 + 2$ A. -2 B. 2 C. 3 D. 1
GIẢI
Vì đề bài không nói rõ x thỏa mãn điều kiện ràng buộc gì nên ta có thể chọn một giá trị bất kì của x để tính giá trị biểu thức T . Ví dụ ta chọn x=2 Khi đó $T = {2^{ – 4 – 1}}f’left( 2 right) – 4ln 2 + 2$ 
$ Rightarrow $ Đáp số chính xác là B Cách tham khảo : Tự luận Tính $f’left( x right) = {2^{{x^2} + 1}}.ln 2.left( {{x^2} + 1} right)’ = 2x.ln {2.2^{{x^2} + 1}}$ và Thế vào $T = {2^{ – {x^2} – 1}}.2xln x{.2^{{x^2} + 1}} – 2xln 2 + 2 = 2xln 2 – 2xln 2 + 2 = 2$ Bình luận • Với bài toán không cho biểu thức ràng buộc của x có nghĩa là x là bao nhiêu cũng được. Ví dụ thay vì chọn x=2 như ở trên, ta có thể chọn x=3 khi đó $T = {2^{ – 9 – 1}}.f’left( 3 right) – 6ln 2 + 2$ kết quả vẫn ra 2 mà thôi. 
• Chú ý công thức đạo hàm $left( {{a^u}} right)’ = {a^u}.ln a.u’$ học sinh rất hay nhầm
VD6-[Báo Toán Học Tuổi Trẻ 2017] Rút gọn biểu thức $frac{{{a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }}}}{{{{left( {{a^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}}$ (với a>0) được kết quả : A. ${a^4}$ B. a C. ${a^5}$ D. ${a^3}$
GIẢI
Ta phải hiểu nếu đáp A đúng thì hiệu $frac{{{a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }}}}{{{{left( {{a^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}} – {a^4}$ phải =0 với mọi giá trị của a Nhập hiệu trên vào máy tính Casio 
Chọn một giá trị a bất kỳ (ưu tiên A lẻ), ta chọn a=1.25 chả hạn rồi dùng lệnh tính giá trị CALC 
Vậy hiệu trên khác 0 hay đáp án A sai Bắt đầu ta kiểm tra tính đúng sai của đáp án A. Nếu đáp án A đúng thì hiệu ${log _6}45 – frac{{a + 2ab}}{{ab}}$ phải bằng 0. Ta nhập hiệu trên vào máy tính Casio và bấm nút = 
Kết quả hiển thị của máy tính Casio là 1 giá trị khác 0 vậy đáp án A sai Để kiểm tra đáp số B ta sửa hiệu trên thành $frac{{{a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }}}}{{{{left( {{a^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}} – a$ Rồi lại tính giá trị của hiệu trên với a=1.25 Vẫn ra 1 giá trị khác 0 vậy B sai. Tương tự vậy ta sẽ thấy hiệu $frac{{{a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }}}}{{{{left( {{a^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}} – {a^5}$ Vậy đáp số C là đáp số chính xác Cách tham khảo : Tự luận Ta rút gọn tử số ${a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }} = {a^{sqrt 3 + 1 + left( {2 – sqrt 3 } right)}} = {a^3}$ Tiếp tục rút gọn mẫu số ${left( {{a^{sqrt 2 – 2}}} right)^{sqrt 2 + 2}} = {a^{left( {sqrt 2 – 2} right)left( {sqrt 2 + 2} right)}} = {a^{2 – 4}} = {a^{ – 2}}$ Vậy phân thức trở thành $frac{{{a^3}}}{{{a^{ – 2}}}} = {a^{3 – left( { – 2} right)}} = {a^5}$ Bình luận • Nhắc lại một số công thức hàm số mũ cơ bản xuất hiện trong ví dụ : ${a^m}.{a^n} = {a^{m + n}}$, ${left( {{a^m}} right)^n} = {a^{m.n}}$ , $frac{{{a^m}}}{{{a^n}}} = {a^{m – n}}$
BÀI TẬP TỰ LUYỆN
Bài 1-[Chuyên Khoa Học Tự Nhiên 2017] Cho ${log _2}left( {{{log }_8}x} right) = {log _8}left( {{{log }_2}x} right)$ thì ${left( {{{log }_2}x} right)^2}$ bằng ? A. 3 B. $3sqrt 3 $ C. 27 D. $frac{1}{3}$
Bài 2-[Chuyên Lam Sơn – Thanh Hóa 2017] Nếu ${log _{12}}6 = a,{log _{12}}7 = b$ thì : A. ${log _2}7 = frac{a}{{1 – b}}$ B. ${log _2}7 = frac{b}{{1 – a}}$ C. ${log _2}7 = frac{a}{{1 + b}}$ D. ${log _2}7 = frac{b}{{1 + a}}$
Bài 3-[Báo Toán Học Tuổi Trẻ 2017] Rút gọn biểu thức $frac{{{a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }}}}{{{{left( {{a^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}}$ (với a>0) được kết quả : A. ${a^4}$ B. a C. ${a^5}$ D. ${a^3}$
Bài 4-[THPT HN Amsterdam 2017] Biến đổi $sqrt[3]{{{x^5}sqrt[4]{x}}}left( {x > 0} right)$ thành dạng lũy thừa với số mũ hữu tỉ, ta được : A. ${x^{frac{{20}}{{21}}}}$ B. ${x^{frac{{21}}{{12}}}}$ C. ${x^{frac{{20}}{5}}}$ D. ${x^{frac{{12}}{5}}}$
Bài 5-[Thi thử Chuyên Sư Phạm lần 1 năm 2017] Tìm x biết ${log _3}x = 4{log _3}a + 7{log _3}b$ : A. $x = {a^3}{b^7}$ B. $x = {a^4}{b^7}$ C. $x = {a^4}{b^6}$ D. $x = {a^3}{b^6}$
Bài 6-[THPT Kim Liên – HN 2017] Cho hàm số $y = 2016.{e^{x.ln frac{1}{8}}}$ . Khẳng định nào sau đây đúng ? A. $y’ + 2yln 2 = 0$ B. $y’ + 3yln 2 = 0$ C. $y’ – 8hln 2 = 0$ D. $y’ + 8yln 2 = 0$
Bài 7-[THPT Nguyễn Trãi – HN 2017] Cho $K = {left( {{x^{frac{1}{2}}} – {y^{frac{1}{2}}}} right)^2}{left( {1 – 2sqrt {frac{y}{x}} + frac{y}{x}} right)^{ – 1}}$ với x>0, y>0. Biểu thức rút gọn của K là ? A. x B. 2x C. x+1 D. x-1
Bài 8-[THPT Phạm Hồng Thái – HN 2017] Cho $a,b > 0;{a^2} + {b^2} = 1598ab$ Mệnh đề đúng là ; A. $log frac{{a + b}}{{40}} = frac{1}{2}left( {log a + log b} right)$ B. $log frac{{a + b}}{{40}} = log a + log b$ C. $log frac{{a + b}}{{40}} = frac{1}{4}left( {log a + log b} right)$ D. $log frac{{a + b}}{{40}} = 2left( {log a + log b} right)$
Bài 9-[Thi Học sinh giỏi tỉnh Phú Thọ năm 2017] Cho các số a>0, b>0, c>0 thỏa mãn ${4^a} = {6^b} = {9^c}$ . Tính giá trị biểu thức $T = frac{b}{a} + frac{b}{c}$ A. 1 B. $frac{3}{2}$ C. 2 D. $frac{5}{2}$
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Bài 1-[Chuyên Khoa Học Tự Nhiên 2017] Cho ${log _2}left( {{{log }_8}x} right) = {log _8}left( {{{log }_2}x} right)$ thì ${left( {{{log }_2}x} right)^2}$ bằng ? A. 3 B. $3sqrt 3 $ C. 27 D. $frac{1}{3}$
GIẢI
Phương trình điều kiện $ Leftrightarrow {log _2}left( {{{log }_8}x} right) – {log _8}left( {{{log }_2}x} right) = 0$ . Dò nghiệm phương trình, lưu vào A 
Thế x=A để tính ${left( {{{log }_2}x} right)^2}$ $ Rightarrow $ Đáp số chính xác là C
Bài 2-[Chuyên Lam Sơn – Thanh Hóa 2017] Nếu ${log _{12}}6 = a,{log _{12}}7 = b$ thì :A. ${log _2}7 = frac{a}{{1 – b}}$ B. ${log _2}7 = frac{b}{{1 – a}}$ C. ${log _2}7 = frac{a}{{1 + b}}$ D. ${log _2}7 = frac{b}{{1 + a}}$
GIẢI
Tính ${log _{11}}6$ rồi lưu vào A Tính ${log _{12}}7$ rồi lưu vào B Ta thấy ${log _2}7 – frac{b}{{1 – a}} = 0$ $ Rightarrow $ Đáp số chính xác là B Bài 3-[Báo Toán Học Tuổi Trẻ 2017] Rút gọn biểu thức $frac{{{a^{sqrt 3 + 1}}.{a^{2 – sqrt 3 }}}}{{{{left( {{a^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}}$ (với a>0) được kết quả : A. ${a^4}$ B. a C. ${a^5}$ D. ${a^3}$
GIẢI
Chọn a>0 ví dụ như a=1.25 chẳng hạn. Tính giá trị $frac{{{{1.25}^{sqrt 3 + 1}}{{.1.25}^{2 – sqrt 3 }}}}{{{{left( {{{1.25}^{sqrt 2 – 2}}} right)}^{sqrt 2 + 2}}}}$ rồi lưu vào A 
Ta thấy $frac{{3125}}{{1024}} = {left( {1.25} right)^5} = {a^5}$ $ Rightarrow $ Đáp số chính xác là C
Bài 4-[THPT HN Amsterdam 2017] Biến đổi $sqrt[3]{{{x^5}sqrt[4]{x}}}left( {x > 0} right)$ thành dạng lũy thừa với số mũ hữu tỉ, ta được : A. ${x^{frac{{20}}{{21}}}}$ B. ${x^{frac{{21}}{{12}}}}$ C. ${x^{frac{{20}}{5}}}$ D. ${x^{frac{{12}}{5}}}$
GIẢI
Chọn a>0 ví dụ như a=1.25 chẳng hạn. Tính giá trị $sqrt[3]{{{{1.25}^5}sqrt[4]{{1.25}}}}$ rồi lưu vào A Ta thấy $A = {left( {1.25} right)^{frac{{21}}{{12}}}} = {a^{frac{{21}}{{12}}}}$ $ Rightarrow $ Đáp số chính xác là B
Bài 5-[Thi thử Chuyên Sư Phạm lần 1 năm 2017] Tìm x biết ${log _3}x = 4{log _3}a + 7{log _3}b$ : A. $x = {a^3}{b^7}$ B. $x = {a^4}{b^7}$ C. $x = {a^4}{b^6}$ D. $x = {a^3}{b^6}$
GIẢI
Theo điều kiện tồn tại của hàm logarit thì ta chọn a,b>0 . Ví dụ ta chọn a=1.25 và b=2.175 Khi đó ${log _3}x = 4{log _3}a + 7{log _3}b Leftrightarrow x = {3^{4{{log }_3}a + 7{{log }_3}b}}$ . 
Thử các đáp án ta thấy $x = {left( {1.125} right)^4}{left( {1.175} right)^7}$ $ Rightarrow $ Đáp số chính xác là B
Bài 6-[THPT Kim Liên – HN 2017] Cho hàm số $y = 2016.{e^{x.ln frac{1}{8}}}$ . Khẳng định nào sau đây đúng ? A. $y’ + 2yln 2 = 0$ B. $y’ + 3yln 2 = 0$ C. $y’ – 8hln 2 = 0$ D. $y’ + 8yln 2 = 0$
GIẢI
Chọn x=1.25 tính $y = 2016.{e^{1.25ln frac{1}{8}}}$ rồi lưu vào A Tính y’(1.25) rồi lưu vào B 
Rõ ràng $B + 3ln 2.A = 0$ → Đáp số chính xác là B
Bài 7-[THPT Nguyễn Trãi – HN 2017] Cho $K = {left( {{x^{frac{1}{2}}} – {y^{frac{1}{2}}}} right)^2}{left( {1 – 2sqrt {frac{y}{x}} + frac{y}{x}} right)^{ – 1}}$ với x>0, y>0. Biểu thức rút gọn của K là ? A. x B. 2x C. x+1 D. x-1
GIẢI
Chọn x=1.125 và y=2.175 rồi tính giá trị biểu thức K 
Rõ ràng $K = frac{9}{8} = 1.125 = x$ $ Rightarrow $ Đáp số chính xác là A
Bài 8-[THPT Phạm Hồng Thái – HN 2017] Cho $a,b > 0;{a^2} + {b^2} = 1598ab$ Mệnh đề đúng là ; A. $log frac{{a + b}}{{40}} = frac{1}{2}left( {log a + log b} right)$ B. $log frac{{a + b}}{{40}} = log a + log b$ C. $log frac{{a + b}}{{40}} = frac{1}{4}left( {log a + log b} right)$ D. $log frac{{a + b}}{{40}} = 2left( {log a + log b} right)$
GIẢI
Chọn a=2 $ Rightarrow $ Hệ thức trở thành $4 + {b^2} = 3196b$ $ Leftrightarrow {b^2} – 3196b + 4 = 0$ . Dò nghiệm và lưu vào B Tính $log frac{{a + b}}{{40}} = log frac{{2 + B}}{{40}}$ Tính tiếp $log a + log b$ Rõ ràng giá trị $log a + log b$ gấp 2 lần giá trị $log frac{{a + b}}{{40}}$ $ Rightarrow $ Đáp số A là chính xác
Bài 9-[Thi Học sinh giỏi tỉnh Phú Thọ năm 2017] Cho các số a>0, b>0, c>0 thỏa mãn ${4^a} = {6^b} = {9^c}$ . Tính giá trị biểu thức $T = frac{b}{a} + frac{b}{c}$ A. 1 B. $frac{3}{2}$ C. 2 D. $frac{5}{2}$
GIẢI
Chọn a=2 Từ hệ thức ta có ${4^2} = {6^b} Leftrightarrow {6^b} – {4^2} = 0$ . Dò nghiệm và lưu vào B Từ hệ thức ta lại có ${9^c} – {4^2} = 0$ . Dò nghiệm và lưu vào C Cuối cùng là tính $T = frac{b}{a} + frac{b}{c} = frac{B}{2} + frac{B}{C} = 2$ $ Rightarrow $ Đáp số chính xác là C 
Tôi là Nguyễn Văn Sỹ có 15 năm kinh nghiệm trong lĩnh vực thiết kế, thi công đồ nội thất; với niềm đam mê và yêu nghề tôi đã tạo ra những thiết kếtuyệt vời trong phòng khách, phòng bếp, phòng ngủ, sân vườn… Ngoài ra với khả năng nghiên cứu, tìm tòi học hỏi các kiến thức đời sống xã hội và sự kiện, tôi đã đưa ra những kiến thức bổ ích tại website nhaxinhplaza.vn. Hy vọng những kiến thức mà tôi chia sẻ này sẽ giúp ích cho bạn!