Tổng Hợp Các Công Thức Toán Lớp 10 Quan Trọng

Trong chương trình Toán học lớp 10, các em học sinh được học rất nhiều kiến thức mới mẻ về đại số và hình học. Kì thi cuối năm sắp tới mà nhiều bạn học sinh vẫn cảm thấy choáng ngợp trước lượng kiến thức mà các em phải học và không biết phải ôn tập bắt đầu từ đâu. Hiểu được điều đó, Kiến Guru đã biên soạn tài liệu tóm tắt các công thức toán lớp 10 dành tặng cho các bạn học sinh.

Tài liệu tóm tắt một cách đầy đủ và ngắn gọn nhất các công thức toán đã học theo hai phần đại số và hình học. Hy vọng, đây sẽ là cẩm nang nhỏ gọn mà đầy đủ kiến thức để các em ôn tập tốt và để dành ôn lại cho những năm học tiếp theo khi quên.

I, Công thức toán lớp 10 phần Đại số

1. Các công thức về bất đẳng thức:

+ Tính chất 1 (tính chất bắc cầu): a > b và b > c a > c

+ Tính chất 2: a > b a + c > b + c

Tức là: Nếu cộng 2 vế của bắt đẳng thức với cùng một số ta được bất đẳng thức cùng chiều và tương đương với bất đẳng thức đã cho.

Hệ quả (Quy tắc chuyển vế): a > b + c a – c > b

+ Tính chất 3:

+ Tính chất 4:

a > b a.c > b.c nếu c > 0

hoặc a > b c.c < b.c nếu c < 0

+ Tính chất 5:

Nếu nhân các vế tương ứng của 2 bất đẳng thức cùng chiều ta được một bất đẳng thức cùng chiều. Chú ý: KHÔNG có quy tắc chia hai vế của 2 bất đẳng thức cùng chiều.

+ Tính chất 6:

a > b > 0 an > bn (n nguyển dương)

+ Tính chất 7:

(n nguyên dương)

+ Bất đẳng thức Cauchy (Cô-si):

Nếu và thì . Dấu = xảy ra khi và chỉ khi: a = b

Tức là: Trung bình cộng của 2 số không âm lớn hơn hoặc bằng trung bình nhân của chúng.

Hệ quả 1: Nếu 2 số dương có tổng không đổi thì tích của chùng lớn nhất khi 2 số đõ bẳng nhau.

Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.

Hệ quả 2: Nếu 2 số dương có tích không đổi thì tổng của chùng nhỏ nhất khi 2 số đó bằng nhau.

Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng diện tích hình vuông có chu vi nhỏ nhất.

+ Bất đẳng thức chứa giá trị trị tuyệt đối:

Từ định nghĩa suy ra: với mọi ta có:

a. |x| 0

b. |x|2 = x2

c. x |x| và -x |x|

Định lí: Với mọi số thực a và b ta có:

|a + b| |a| + |b| (1)

|a – b| |a| + |b| (2)

|a + b| = |a| + |b| khi và chỉ khi a.b 0

|a – b| = |a| + |b| khi và chỉ khi a.b 0

2. Các công thức về phương trình bậc hai:

a. Công thức nghiệm của phương trình bậc hai:

: Phương trình vô nghiệm. : Phương trình có nghiệm kép:

: Phương trình có 2 nghiệm phân biệt:

;

b. Công thức nghiệm thu gọn của phương trình bậc hai:

Nếu “b chẵn” (ví dụ ) ta dùng công thức nghiệm thu gọn.

: Phương trình vô nghiệm. : Phương trình có nghiệm kép: : Phương trình có 2 nghiệm phân biệt:

;

Chú ý: với là hai nghiệm của phương trình bậc 2:

c. Định lí Viet:

Nếu phương trình bậc 2 có 2 nghiệm thì:

d. Các trường hợp đặc biệt của phương trình bậc 2:

– Nếu thì phương trình có nghiệm: – Nếu thì phương trình có nghiệm:

e. Dấu của nghiệm số:

– Phương trình có 2 nghiệm trái dấu:

– Phương trình có 2 nghiệm dương phân biệt:

– Phương trình có 2 nghiệm âm phân biệt

3. Các công thức về dấu của đa thức:

a. Dấu của nhị thức bậc nhất:

trái dấu a 0 cùng dấu a

“Phải cùng, trái trái”

b. Dấu của tam thức bậc hai:

△<0 : f(x) cùng dấu với hệ số a

△=0 : f(x) cùng dấu với hệ số a với mọi

△=0 : f(x) có 2 nghiệm x1 , x2

x1 x2

F(x)

cùng dấu a 0 trái dấu a 0 cùng dấu a

c. Dấu của đa thức bậc ≥ 3: Bắt đầu từ ô bên phải cùng dấu với hệ số a của số mũ cao nhất, qua nghiệm đơn đổi dấu, qua nghiệm kép không đổi dấu.

4. Các công thức về điều kiện để tam thức không đổi dấu trên R.

Cho tam thức bậc hai:

5. Các công thức toán lớp 10 về phương trình và bất phương trình chứa trị tuyệt đối

a. Phương trình :

b. Bất phương trình:

6. Các công thức toán lớp 10 về phương trình và bất phương trình chứa ẩn dưới dấu căn bậc hai

a. Phương trình:

b. Bất phương trình:

7. Các công thức toán lớp 10 lượng giác

a. Định nghĩa giá trị lượng giác:

b. Các công thức lượng giác cơ bản:

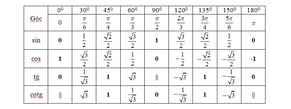
c. Các giá trị lượng giác đặc biệt:

d. Công thức cộng:

e. Công thức nhân đôi:

f. Công thức hạ bậc:

g. Công thức nhân ba:

h. Công thức biến đổi tích thành tổng:

i. Công thức biến đổi tổng thành tích:

k. Cung liên kết: Sin – bù; cos – đối; phụ – chéo; hơn kém – tan, cot.

– Hai cung bù nhau: và

– Hai cung đối nhau: và

– Hai cung phụ nhau: và

– Hai cung hơn kém : và

– Hai cung hơn kém : và

l. Công thức tính theo :

Nếu đặt thì:

m. Một số công thức khác:

II. Công thức toán lớp 10 phần Hình học

1. Các công thức toán lớp 10 về hệ thức lượng trong tam giác:

Cho , ký hiệu

– a, b, c: độ dài 3 cạnh – R: bán kính đường tròn ngoại tiếp

Định lí côsin:

Định lí sin:

Công thức tính độ dài trung tuyến:

2. Các công thức toán lớp 10 về hệ thức lượng trong tam giác vuông

3. Các công thức tính diện tích:

Tam giác thường:

(: độ dài 3 đường cao)

(r: bán kính đường tròn nội tiếp, : nửa chu vi)

(Công thức Hê-rông)

Tam giác vuông: x tích 2 cạnh góc vuông

Tam giác đều cạnh a:

Hình vuông cạnh a:

Hình chữ nhật:

Hình bình hành: hoặc

Hình thoi: hoặc hoặc

x tích 2 đường chéo

Hình tròn:

4. Công thức toán 10 về phương pháp tọa độ trong mặt phẳng Oxy

a. Ứng dụng tích vô hướng của hai vectơ

Cho ba điểm: . Ta có:

– Tọa độ véctơ

– Tọa độ trung điểm I của AB là: .

– Tọa độ trọng tâm G của là: .

Cho các vec-tơ và các điểm :

b. Phương trình của đường thẳng :

Cho là VTCP của d., là VTPT của d .

Điểm M( thuộc d.

– PT tham số của d: =

– PT chính tắc của d:

– PT tổng quát của d: hoặc:

c. Khoảng cách:

+ Khoảng cách từ điểm M(x0, y0) đến đương thẳng (d) : Ax + By + C = 0

+ Khoảng cách giữa hai đường thẳng song song: Ax + By + C1 = 0 và Ax + By + C2 = 0

d. Vị trí tương đối 2 đường thẳng:

(d1) : A1 x + B1 y + C1 = 0, (d2) : A2 x + B2 y + C2 = 0

e. Góc giữa 2 đường thẳng:

(d1) : A1 x + B1 y + C1 = 0, (d2) : A2 x + B2 y + C2 = 0,

d. Phương trình đường phân giác của góc tạo bởi 2 đường thẳng (d1)và (d2):

(góc nhọn lấy dấu – , góc tù lấy dấu + )

e. Phương trình đường tròn :

Đường tròn tâm I(a ; b), bán kính R có phương trình :

Dạng 1 :

Dạng 2 :

, điều kiện :

Trên đây là tài liệu tổng hợp các công thức toán lớp 10 đầy đủ các kiến thức đã học trong chương trình toán 10. Các công thức được biên soạn cụ thể theo từng chương, từng bài rất phù hợp để các em học sinh dễ dàng học thuộc. Với bộ công thức ngắn gọn này, hy vọng sẽ giúp các em sẽ ôn tập hiệu quả, hoàn thành tốt những bài kiểm tra sắp tới của mình và là người bạn đồng hành cùng các em trong các năm học phổ thông.