Bài Tập Lượng Giác Lớp 10 Cơ Bản Có Đáp Án Chi Tiết

Trong chương trình Toán đại số lớp 10, ở chương cuối cùng các em học sinh sẽ được làm quen với một chuyên ngành khá hấp dẫn nhưng cũng không kém phần phức tạp của Toán học. Đó chính là chương Lượng giác. Để giúp các em học tốt chương lượng giác, Kiến Guru đã chọn lọc các bài tập lượng giác lớp 10 cơ bản có đáp án. Các bài tập sẽ xoay quanh các nội dung: cung và góc lượng giác, các công thức lượng giác và các phép biến đổi lượng giác. Không chỉ liệt kê các dạng bài tập mà trong tài liệu chúng tôi còn củng cố lại các lý thuyết trọng tâm của chương để các em có thể ôn tập trước khi làm bài. Đặc biệt, các bài tập trong tài liệu còn kèm theo đáp án chi tiết để các em thuận lợi trong việc tra cứu lời giải cũng như giải đáp thắc mắc những dạng chưa làm được. Hy vọng rằng sau khi làm xong những bài tập này, các bạn học sinh lớp 10 có thể nắm vững các dạng bài tập lượng giác. Qua đó, hoàn thành tốt các bài kiểm tra cũng như là nền tảng tiếp thu các lý thuyết lượng giác mở rộng hơn ở lớp 11.

Tài liệu bao gồm các dạng toán về lượng giác. Trong mỗi phần trước hết sẽ nhắc lại lý thuyết, sau đó là phương pháp giải và các bài tập có kèm theo lời giải chi tiết.

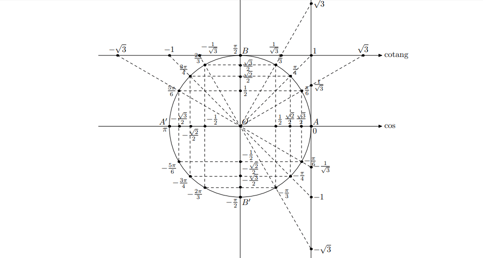
I. Bài tập về các hệ thức lượng giác cơ bản.

Trong tài liệu bài tập lượng giác lớp 10 cơ bản có đáp án thì đây là dạng bài tập dễ nhất vì các hệ thức lượng giác cơ bản này chúng ta đã học trong chương trình lớp 9. Lên lớp 10, bằng việc kết hợp các hệ thức cơ bản này với cách xác định tính âm dương của các giá trị lượng giác trên đường tròn lượng giác, ta có thể dễ dàng tính tất cả các giá trị lượng giác của góc khi chỉ biết một giá trị lượng giác nào đó.

Bài tập 1: Cho 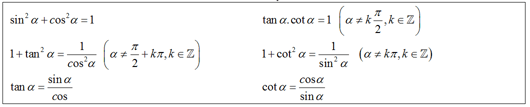. Xác định tính âm dương của các giá trị lượng giác:

Hướng dẫn: Xác định điểm cuối của các cung ,… thuộc cung phần tư nào, từ đó xác định tính âm dương của các giá trị lượng giác tương ứng.

+ Cách xác định tính âm dương của các giá trị lượng giác

Giải

Bài tập 2: Tính các giá trị lượng giác của góc α biết:

Hướng dẫn:

+ Nếu biết trước sinα thì dùng công thức: sin2α + cos2α = 1 để tìm ,

lưu ý:xác định dấu của các giá trị lượng giác để nhận, loại.

+ Nếu biết trước cosα thì tương tự như trên.

+ Nếu biết trước tanα thì dùng công thức: để tìm cosα ,

lưu ý: xác định tính âm dương của các giá trị lượng giác để nhận, loại. sinα = tanα.cosα ,

Giải

Các bài tập còn lại làm tương tự.

Bài tập 3: Chứng minh đẳng thức lượng giác: (dùng các hằng đẳng thức đại số và các hằng đẳng thức lượng giác cơ bản để biến đổi một vế thành vế kia)

Hướng dẫn:

Nhận xét: Trong tài liệu bài tập lượng giác lớp 10 cơ bản có đáp án thì đây là một dạng bài khá hay vì nó kết hợp giữa các hằng đẳng thức đại số và các công thức lượng giác. Để nhận dạng các bài tập loại này các em cần lưu ý các hằng đẳng thức mà chúng ta thường gặp là:

Bài tập 4: Đơn giản các biểu thức sau:

Bài tập 5: Cho . Tính:

Hướng dẫn: Để tính các biểu thức này ta phải biến đổi chúng về một biểu thức theo tana rồi thay giá trị của tan a vào biểu thức đã biến đổi.

Bài tập 6: Cho . Tính:

Hướng dẫn:

Bài tập 7: Cho và . Tính:

Hướng dẫn:

Bài tập 8: Cho

Hướng dẫn: Biến đổi biểu thức A theo sin2α

Bài tập 9:

a) Tính biết tanα = -3

b) Tính biết cotα = 2

Hướng dẫn: a) Chia cả tử và mẫu cho cosα

b) Chia cả tử và mẫu cho sinα

II. Bài tập rút gọn và tính giá trị của biểu thức lượng giác

Trong phần này, chúng ta sẽ tìm hiểu các bài tập lượng giác lớp 10 cơ bản có đáp án liên quan đến rút gọn và tính giá trị biểu thức. Các biểu thức ở đây đều chứa các góc có mối liên hệ đặc biệt với nhau, khi ta áp dụng các công thức lượng giác liên quan giữa các góc đặc biệt này thì cũng sẽ triệt tiêu nhau dẫn đến một đáp số ngắn gọn hơn biểu thức ban đầu.

+ Dùng các hệ thức cơ bản và giá trị lượng giác của các góc có mối liên hệ đặc biệt

+ Chú ý: k € Z ta có:

sin(α + k2π) = sin α

cos(α + k2π) = cosα

tan(α + kπ) = tanα

cot(α + kπ) = cotα

Bài tập 1: Đơn giản các biểu thức:

Hướng dẫn:

Hướng dẫn:

Bài tập 2: Tính:

Hướng dẫn:

Hướng dẫn:

tương tự những phần còn lại nên cos20o + cos160o = 0 )

III. Bài tập về các công thức lượng giác

Trong tài liệu bài tập lượng giác lớp 10 cơ bản có đáp án mà chúng tôi giới thiệu, thì đây là dạng bài tập khó nhất, yêu cầu học sinh phải nắm vững các công thức lượng giác để biến đổi chúng một cách linh hoạt nhất. Dưới đây, chúng tôi xin nhắc lại các công thức lượng giác quen thuộc trong chương trình lớp 10 để các bạn có thể ôn tập lại và vận dụng.

Bài tập 1: Tính các giá trị lượng giác của các cung có số đo:

Hướng dẫn: Phân tích thành tổng hoặc hiệu của hai cung đặc biệt

Phân tích 15o = 60o – 45o hoặc 45o – 30o rồi sử dụng các công thức cộng

Phân tích rồi sử dụng các công thức cộng

Bài tập 2: Chứng minh rằng:

Hướng dẫn: biến đổi VP thành vế trái

Hướng dẫn:

Bài tập 3: Biết và . Hãy tính các giá trị lượng giác của góc:

Bài tập 4: Tính cos2α, sin2α, tan2α biết:

Hướng dẫn:

a) tính sina, sau đó áp dụng các công thức nhân đôi.

Bài tập 5: Chứng minh các đẳng thức sau:

Hướng dẫn:

Từ (1) và (2) suy ra đpcm

Hướng dẫn:

Hướng dẫn:

Hướng dẫn:

Hướng dẫn:

Hướng dẫn:

Hướng dẫn:

Hướng dẫn: Tương tự như câu c

Hướng dẫn: Sử dụng hằng đẳng thức a3 – b3

Hướng dẫn: Quy đồng mẫu

Hướng dẫn: sin2a=2sinacosa; đặt nhân tử chung sau đó áp dụng

Hướng dẫn:

Hướng dẫn:

Hướng dẫn:

Hướng dẫn:

cos4α = 2 cos22α – 1 sau đó sử dụng cos2α – 1 = -2sin2α

Hướng dẫn:

Hướng dẫn:

Sử dụng công thức hạ bậc

Bài tập 6: Chứng minh các biểu thức sau là những hằng số không phụ thuộc vào a

a) A = 2(sin6α + cos66α) – 3(sin4α + cos4α)

Hướng dẫn: Sử dụng a3 + b3; A = -1

b) B = 4(sin4α + cos4α) – cos4α

Hướng dẫn: Sử dụng a2 + b2 = (a + b)2 – 2ab và cos2α = 1 – 2sin2a; B = 3

Hướng dẫn: Sử dụng

Bài tập 7: Tính các biểu thức:

Hướng dẫn:

Kiến Guru vừa giới thiệu xong cho các bạn các dạng bài tập lượng giác lớp 10 cơ bản có đáp án. Đây là các dạng bài tập điển hình trong chương trình lượng giác lớp 10. Bài tập được phân thành các dạng từ thông hiểu đến vận dụng cao, phù hợp với các đối tượng học sinh từ trung bình yếu đến khá giỏi. Để làm tốt các dạng bài tập rút gọn biểu thức, chứng minh biểu thức lượng giác, các bạn cần phải ghi nhớ kĩ các công thức lượng giác và làm thật nhiều bài tập để rèn khả năng biến đổi linh hoạt. Bài tập có kèm theo lời giải chi tiết để các bạn có thể tra cứu đáp số và học được cách trình bày một bài toán lượng giác như thế nào. Hy vọng đây sẽ là một tài liệu hữu ích để các bạn học sinh lớp 10 vừa ôn lại lý thuyết, vừa rèn luyện kĩ năng giải bài tập và nâng cao khả năng biến đổi lượng giác. Đồng thời, tài liệu này cũng sẽ là bạn đồng hành khi các em lên lớp 11 nếu lỡ quên đi một phần nào đó. Lượng giác là một nội dung mới lạ và hấp dẫn. Nó không hề khó nếu chúng ta chăm chỉ học thuộc các công thức biến đổi. Chúc các em học sinh sẽ nâng cao kiến thức lượng giác của mình sau khi đọc xong tài liệu này.