Trong chương trình toán học cấp trung học cơ sở, phương trình vô nghiệm là một trong những dạng toán tương đối khó với các bạn học sinh. Qua bài viết này, Bamboo School sẽ giúp những bạn chưa nắm được phương trình vô nghiệm sẽ có một nền tảng kiến thức thật tốt và kỹ năng giải phương trình cũng như những dạng bài tập của phương trình vô nghiệm. Hy vọng giúp các bạn học sinh rèn luyện thêm kiến thức để chuẩn bị cho các kì thi sắp tới. Các bạn đã sẵn sàng khám phá cùng Bamboo School chưa nào?
Phương trình vô nghiệm là gì?
Phương trình vô nghiệm là khi:
- Phương trình không sở hữu nghiệm nào.
- Phương trình vô nghiệm có tập nghiệm là S = Ø
- Một phương trình hoàn toàn có thể có một nghiệm, hai nghiệm, ba nghiệm,… nhưng cũng hoàn toàn có thể không có nghiệm nào hoặc vô số nghiệm .
Khi nào thì phương trình vô nghiệm?
Bất phương trình vô nghiệm <=> a=0 và b xét với dấu > thì b ≤0≤0; với dấu < thì b ≥0.
Điều kiện để phương trình vô nghiệm
Phương trình bậc nhất một ẩn: ax + b = 0
- a ≠ 0 thì phương trình có nghiệm duy nhất x = -b/a
- a = 0 và b ≠ 0 thì phương trình vô nghiệm
- a = 0 và b = 0 thì phương trình vô số nghiệm
Phương trình bậc hai một ẩn: ax^2 + bx + c = 0
- a = 0 thì phương trình trở thành bx + c = 0
- a ≠ 0
∆ > 0 thì phương trình có 2 nghiệm phân biệt x1/2 = (-b±√∆)/2a
∆ = 0 thì phương trình có nghiệm kép x = -b/2a
∆ < 0 thì phương trình vô nghiệm
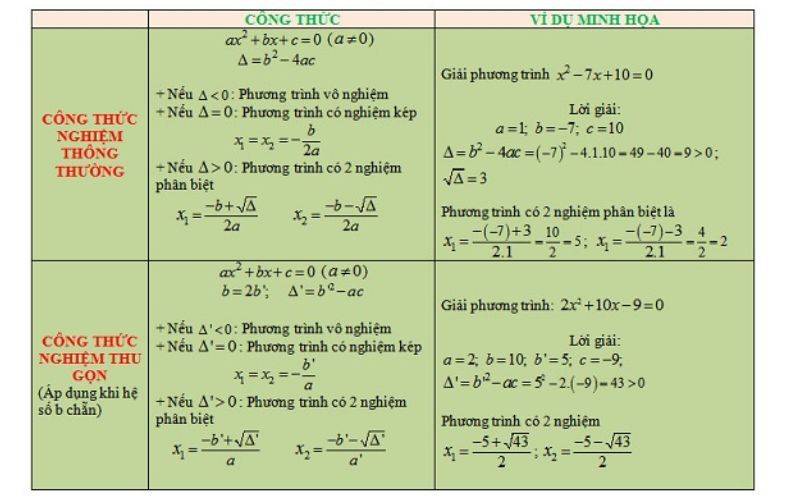
Công thức giải phương trình vô nghiệm
Phương trình bậc nhất một ẩn:
Xét phương trình bậc nhất có dạng ax + b = 0 .Nếu a = 0, b ≠ 0 thì phương trình vô nghiệm .
Phương trình bậc hai một ẩn:
Xét phương trình bậc hai có dạng ( a ≠ 0 ) .
- Công thức nghiệm tính delta (ký hiệu là ∆).
Nếu ∆ < 0 thì phương trình vô nghiệm .
- Công thức nghiệm thu gọn tính ∆’ (chỉ tính ∆’ khi hệ số b chẵn).
Với b = 2 b ’
Nếu ∆ ’ < 0 thì phương trình vô nghiệm .
Các dạng bài tập tìm m để phương trình vô nghiệm
Bài tập 1: Tìm m để phương trình mx^2 – 2(m – 1)x + m + 1 = 0 vô nghiệm
Hướng dẫn: Do hệ số ở biến x^2 có chứa tham số m, nên khi giải bài toán ta phải chia hai trường hợp là m = 0 và m ≠ 0.
Lời giải: Bài toán được chia thành 2 trường hợp:
- TH1: m = 0
Phương trình trở thành phương trình bậc nhất một ẩn 2x + 1 = 0 ⇔ x = -½ (loại)
Với m = 0 thì phương trình mx^2 – 2(m – 1)x + m + 1 = 0 có nghiệm x = -½
- TH2: m ≠ 0
Phương trình trở thành phương trình bậc hai một ẩn: mx^2 – 2(m – 1)x + m + 1 = 0
Để phương trình vô nghiệm thì ∆’ < 0
⇔ (m – 1)^2 – m.(m + 1) < 0
⇔ m^2 – 2m + 1 – m^2 – m < 0
⇔ -3m < -1
⇔ m > ⅓
Vậy với m > ⅓ thì phương trình mx^2 – 2(m – 1)x + m + 1 = 0 vô nghiệm
Bài tập 2: Tìm m để phương trình 5×2 – 2x + m = 0 vô nghiệm
Hướng dẫn: Do hệ số ở biến x^2 là một số khác 0 nên phương trình là phương trình bậc hai một ẩn. Ta sẽ áp dụng điều kiện để phương trình bậc hai một ẩn vô nghiệm vào giải bài toán.
Lời giải: Để phương trình 5x^2 – 2x + m = 0 vô nghiệm thì ∆’ < 0
⇔ 4 – 5m < 0
⇔ m > ⅘
Vậy với m > ⅘ thì phương trình 5x^2 – 2x + m = 0 vô nghiệm
Bài tập 3: Tìm m để phương trình 3×2 + mx + m2 = 0 vô nghiệm
Hướng dẫn: Do hệ số ở biến x2 là một số khác 0 nên phương trình là phương trình bậc hai một ẩn. Ta sẽ áp dụng điều kiện để phương trình bậc hai một ẩn vô nghiệm vào giải bài toán.
Lời giải: Để phương trình 3×2 + mx + m2 = 0 vô nghiệm thì ∆ < 0
⇔ m^2 – 4.3.m^3 < 0
⇔ -11m^2 < 0∀m ≠ 0
Vậy với mọi m ≠ 0 thì phương trình 3×2 + mx + m2 = 0 vô nghiệm.
Bài tập 4: Tìm m để phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm
Hướng dẫn: Do hệ số ở biến x2 có chứa tham số m, nên khi giải bài toán ta phải chia hai trường hợp là m = 0 và m ≠ 0.
Lời giải:
- TH1: m = 0
Phương trình trở thành phương trình bậc nhất một ẩn 0x = -3 (phương trình vô nghiệm)
Với m = 0 thì phương trình vô nghiệm
- TH2: m ≠ 0
Để phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm thì ∆’ < 0
⇔ (-m^2)^2 – m^2 (4m^2 + 6m + 3) < 0
⇔ -3m^4 – 6m^3 – 3m^2 < 0
⇔ -3m^2 .(m^2 + 2m +1) < 0
⇔ -3m^2 .(m+1)^2 < 0∀m ≠ m-1
Vậy với mọi m ≠ – 1 thì phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm
Thông qua bài viết, chắc hẳn các bạn học sinh cũng ít nhiều nắm được những ý chính về phương trình vô nghiệm cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ?. Bamboo School hy vọng thông qua bài viết này, các bạn đã có nền tảng kiến thức thật tốt về phương trình vô nghiệm cũng như kỹ năng giải phương trình. Đừng quên luyện tập mỗi ngày để nhanh chóng tiến bộ nhé. Chúc các bạn học tập thật tốt!