Hoán vị, chỉnh hợp và tổ hợp: Công thức và các dạng chi tiết

Bài viết dưới đây giúp các bạn trả lời các câu hỏi: Hoán vị là gì? Chỉnh hợp là gì? Tổ hợp là gì?. Bên cạnh đó là các công thức, các dạng toán và phương pháp giải chi tiết.

I. HOÁN VỊ LÀ GÌ?

Để cho dễ hình dung, ta có thể tạm hiểu: Hoán trong từ hoán đổi, vị trong từ vị trí. Có nghĩa là nếu chúng ta có 1 tập hợp n phần tử (n>0). Thì mỗi cách sắp xếp n phần tử đó theo một thứ tự thì ta được 1 hoán vị của n phần tử đó.

Chẳng hạn như xếp ba bạn HOÀNG, bạn XUÂN và bạn ĐỊNH vào một bàn học ngang. Ta có một hoán vị HOÀNG-XUÂN-ĐỊNH. Và hoán vị ĐỊNH-HOÀNG-XUÂN là hoán vị khác với hoán vị HOÀNG-XUÂN-ĐỊNH.

Ở trên ta đã có định nghĩa của một hoán vị. Vậy câu hỏi tự nhiên đặt ra là có bao nhiêu hoán vị? Chúng ta có thể dễ dàng trả lời câu hỏi đó bằng cách áp dụng quy tắc nhân.

Số hoán vị: Cho tập hợp gồm n phần tử (n>0). Hỏi có bao nhiêu hoán vị của n phần tử đó?

Giả sử ta có n vị trí đánh số từ 1 tới n. Để được 1 hoán vị của n phần tử đã cho, ta xếp từng phần tử lần lượt vào các vị trí từ 1 đến n. Xếp vào vị trí thứ 1 có n cách. Xếp vào vị trí thứ 2 có n-1 cách (vì 1 phần tử đã xếp vào vị trí thứ 1 rồi). Cứ như vậy đến hết. Vậy số hoán vị của n phần tử đã cho là

Tôi muốn nhấn mạnh với các bạn sự khác nhau giữa hoán vị và số hoán vị. Đó là điều mà các bạn thường không để ý và bỏ qua.

II. HOÁN VỊ LẶP LÀ GÌ?

Xét ví dụ sau: Từ các chữ số 1, 2, 3, 4 lập được bao nhiêu số tự nhiên có 9 chữ số sao cho chữ số 1 xuất hiện đúng một lần, chữ số 2 xuất hiện đúng ba lần, chữ số 3 xuất hiện đúng 2 lần, chữ số 4 xuất hiện đúng 3 lần?

Khi đó số 122233444 thỏa mãn yêu cầu bài toán. Nếu ở số trên mà ta hoán vị 2 chữ số 3 chẳng hạn thì số không đổi. Do đó vẫn là 1 số thỏa mãn yêu cầu bài toán mà thôi. Dạng bài toán tương tự như ví dụ trên gọi là hoán vị lặp.

Vậy đếm số hoán vị lặp như thế nào?

Giả sử một tập hợp có k phần tử được đánh số từ 1 đến k. Một cách sắp xếp k phần tử đó sao cho phần tử thứ i (1≤i≤k) xuất hiện n(i) lần và n(1)+n(2)+…+n(k)=n được gọi là một hoán vị lặp của k phần tử. Số hoán vị lặp là

Quay lại ví dụ trên ta thấy số các số tự nhiên thỏa mãn là

III. TỔ HỢP LÀ GÌ?

Ta có thể hiểu mỗi một tập con gồm k phần tử của tập hợp gồm n phần tử (n>0) là một tổ hợp chập k của n.

Ví dụ ta có tập hợp 7 viên ngọc rồng đánh số từ 1 đến 7. Một tổ hợp chập 3 của 7 được minh họa như hình.

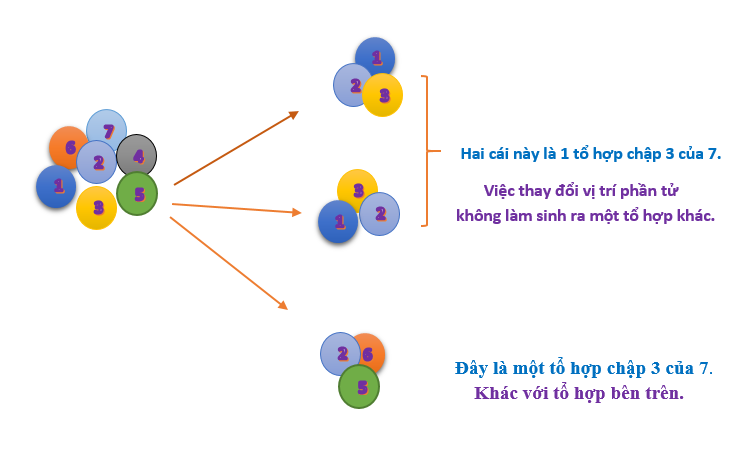
Số tổ hợp chập k của n: Để đếm số tổ hợp chập k của n ta giả sử có k vị trí đánh số từ 1 đến k. Lấy một phần tử xếp vào vị trí thứ nhất có n cách. Lấy tiếp 1 phần tử xếp vào vị trí số 2 có n-1 cách…cứ như vậy đến phần tử thứ k có n-k+1 cách. Khi đếm như vậy thì k phần tử đó có thể hoán đổi (hoán vị) với nhau mà không sinh ra tổ hợp khác. Vậy số tổ hợp chập k của n là

IV. CHỈNH HỢP LÀ GÌ?

Ta có thể hiểu một cách sắp xếp các phần tử của một tập con gồm k phần tử của tập hợp gồm n phần tử là một chỉnh hợp chập k của n.

Để dễ dàng phân biệt tổ hợp và chỉnh hợp ta quay lại ví dụ 7 viên ngọc rồng ở phần trên. Ở đây lấy ra 3 viên ngọc và sắp theo thứ tự từ trái qua phải. Một chỉnh hợp chập 3 của 7 được minh họa như hình.

Như vậy ta có thể phân biệt chỉnh hợp và tổ hợp rằng chỉnh hợp chập k thì có kể đến thứ tự của k phần tử, còn tổ hợp thì không kể đến thứ tự.

Số chỉnh hợp chập k của n: Để đếm số tổ hợp chập k của n ta giả sử có k vị trí đánh số từ 1 đến k. Lấy lần lượt các phần tử xếp vào các vị trí. Mỗi vị trí 1 phần tử ta được một chỉnh hợp chập k của n phần tử. Lấy một phần tử xếp vào vị trí thứ nhất có n cách. Lấy tiếp 1 phần tử xếp vào vị trí số 2 có n-1 cách…cứ như vậy đến phần tử thứ k có n-k+1 cách. Vậy số chỉnh hợp chập k của n là

V. LIÊN HỆ GIỮA HOÁN VỊ CHỈNH HỢP TỔ HỢP

Theo các định nghĩa bên trên ta có thể thấy tổ hợp chỉnh hợp hoán vị có mối liên hệ với nhau. Cụ thể một chỉnh hợp chập k của n được tạo thành bằng cách thực hiện 2 bước. Bước 1 là lấy 1 tổ hợp chập k của n phần tử. Bước 2 là hoán vị k phần tử đó. Vì vậy ta có công thức liên hệ giữa chỉnh hợp tổ hợp hoán vị như sau:

Trên đây là một số định nghĩa trong chương chỉnh hợp tổ hợp xác xuất mà toanthaydinh.com giới thiệu đến các bạn. Thời gian tới tôi sẽ tiếp tục cập nhật các dạng toán tổ hợp chỉnh hợp ở đây. Tổ hợp chỉnh hợp xác suất là nội dung thường xuất hiện ở kỳ thi THPT QG ở mức độ nhận biết thông hiểu. Vì vậy các bạn hãy nắm chắc các khái niệm trong nội dung xác suất tổ hợp chỉnh hợp để giải toán nhé!. Chúc các bạn học giỏi và thành công!

Xem thêm:

Nhị thức Newton: Công thức và một số bài toán

Chỉnh hợp lặp và chỉnh hợp không lặp

Bài tập hoán vị chỉnh hợp tổ hợp có lời giải (Key)

Tổ hợp xác suất –

• Nhị thức Newton: Công thức và một số bài toán

• Quy tắc đếm: Quy tắc cộng và quy tắc nhân