Phương pháp chứng minh 2 góc bằng nhau

I. Phương pháp chứng minh 2 góc bằng nhau theo từng khối lớp1. Chứng minh theo kiến thức Hình học lớp 6Vận dụng tính chất của tia phân giác: Tia Oz là tia phân giác của góc xOy (Oz nằm giữa tia Ox và tia Oy) => Góc xOy = góc zOy = 1⁄2 góc xOy.=> Như vậy: Hai góc cần chứng minh là hai góc tạo bởi tia phân giác của góc cho trước.

2. Chứng minh theo kiến thức Hình học lớp 7* Phương pháp 1: Vận dụng tính chất góc ở đấy của tam giác cân và hai góc của tam giác đều.Ví dụ:- Khi tam giác ABC cân: góc B = góc C- Khi tam giác ABC đều: góc A = góc B = góc C.* Phương pháp 2: Vận dụng hai tam giác bằng nhau => Hai góc tương ứng của hai tam giác bằng nhau sẽ bằng nhau.Ví dụ:Tam giác ABC = tam giác A’B’C’ => Góc A bằng góc A’; góc B = góc B’; góc C = góc C’* Phương pháp 3: Vận dụng tính chất của hai góc đối đỉnh: Hai góc đối đỉnh thì bằng nhau* Phương pháp 4: Vận dụng tính chất của hai đường thẳng song song:Nếu một đường thẳng cắt hai đường thẳng đã cho và trong các góc tạo thành có một cặp góc so le trong bằng nhau, thì:- Hai góc đồng vị bằng nhau.- Hai góc so le trong còn lại bằng nhau.- Hai góc trong cùng phía bù nhau.* Phương pháp 5: Vận dụng tính chất của hai góc có cạnh tương ứng song song (vuông góc) cùng nhọn hoặc cùng tù).* Phương pháp 6: Khi trên hình có góc thứ 3 bằng cả 2 góc đó, ta chuyển về bài toán chứng minh hai góc cùng bằng góc thứ ba => Hai góc đó bằng nhau.Ví dụ: Trong tam giác ABC, có:- Góc A = góc B- Góc C = góc B=> Góc A = góc B.* Phương pháp 7: Khi trên hình có góc vuông hoặc có ba điểm thẳng hàng, ta chứng minh hai góc cùng phụ (hoặc cùng bù) với góc thứ 3 => Hai góc bằng nhau.* Phương pháp 8: Khi có một tia nằm giữa hai tia còn lại, ta chứng minh hai góc cùng bằng tổng hoặc hiệu của hai cặp góc tương ứng bằng nhau => Hai góc đó bằng nhau.3. Chứng minh theo kiến thức Hình học lớp 8* Phương pháp 1: Vận dụng tính chất về góc của các tứ giác đặc biệt- Trong hình bình hành, các góc đối bằng nhau.- Trong hình vuông, bốn góc vuông bằng nhau.* Phương pháp 2: Vận dụng hai góc tương ứng của hai tam giác đồng dạng- Hai tam giác đồng dạng với nhau khi chúng có các góc tương ứng bằng nhau.4. Chứng minh theo kiến thức Hình học lớp 9* Phương pháp 1: Áp dụng tính chất của tứ giác nội tiếp* Phương pháp 2: Áp dụng tính chất của góc nội tiếp, góc ở tâm, góc giữa tia tiếp tuyến và dây cung cùng chắn một cung trong đường tròn hay hai đường tròn bằng nhau.

II. Một số bài tập minh họa chứng minh 2 góc bằng nhauBài tập 1: Cho tam giác ABC, lấy D là trung điểm của AC. Từ A vẽ đường thẳng song song với BC, cắt BD tại E. Tại cạnh BC lấy điểm M sao cho DM cắt AE tại N. Chứng minh rằng:a) góc AED = góc CBDb) góc DNE = góc DMBc) góc BAD = góc DCE.Hướng dẫn giải: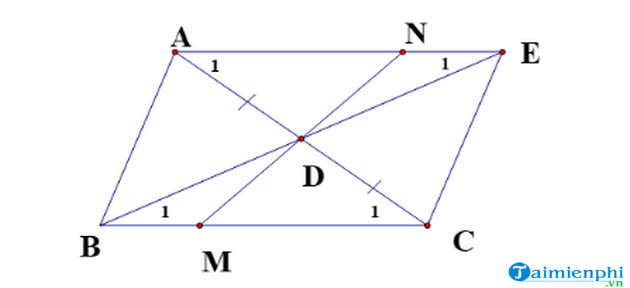a) Chứng minh: góc AED = góc CBDXét tam giác ADE và tam giác CDB, có:góc DAE = góc DCB (vì hai góc so le trong)DA = DC (D là trung điểm của AC)góc ADE = góc CDB (hai góc đối đỉnh)=> Tam giác ADE = tam giác CDB (g.c.g)=> Góc AED = góc CBD (điều phải chứng minh)Câu b); câu c): Học sinh tự giải (tương tự như phương pháp giải các câu trên).

Bài tập 2: Cho tam giác ABC có 3 góc đều là góc nhọn, AB < ac,=”” m=”” là=”” trung=”” điểm=”” của=”” ac.=”” trên=”” tia=”” đối=”” của=”” tia=”” mb,=”” lấy=”” điểm=”” d=”” sao=”” cho:=”” bm=””>a) AB = CDb) góc ABM = góc CDMc) Vẽ AH, CK vuông với BD (H, K thuộc BD). Chứng minh: góc ABH = góc CDK.Hướng dẫn giải:a) Chứng minh AB = CDXét tam giác ABM và tam giác CDM, có:MA = MC (đề bài đã cho)MB = MD (đề bài đã cho)góc AMB = góc DMC (đối đỉnh)=> Tam giác ABM = tam giác CDM (c.g.c)=> AB = CD (điều phải chứng minh).b) Chứng minh: góc ABM = góc CDMVì hai tam giác ABM và CDM bằng nhau (đã chứng minh ở câu a)=> góc ABM = góc CDM (điều phải chứng minh).c) Chứng minh: góc ABH = góc CDKXét tam giác ABH và tam giác CDK, có:góc AHB = góc CKD (đều là góc vuông)AB = CD (do tam giác ABM = tam giác CDM)góc ABH = góc KDC=> Tam giác ABH = tam giác CDK (cạnh huyền.góc nhọn)=> góc ABH = góc CDK (điều phải chứng minh).