✅ Cách giải phương trình chứa dấu căn ⭐️⭐️⭐️⭐️⭐️

Cách giải phương trình chứa dấu căn và Bài tập vận dụng – Toán lớp 9

Căn thức (căn bậc 2, căn bậc 3) là nội dung kiến thức mà các em học ở ngay chương 1 đại số lớp 9, phần bài tập về căn thức cũng thường xuyên xuất hiện trong đề thi tuyển sinh vào lớp 10 THPT.

Có nhiều dạng bài tập về căn thức như: rút gọn biểu thức, tính giá trị của biểu thức, giải phương trình, hệ phương trình,… Tuy nhiên, trong bài viết này chúng ta tập trung tìm hiểu cách giải phương trình chứa dấu căn, qua đó vận dụng giải một số bài tập về phương trình chứa căn thức để rèn luyện kỹ năng giải toán.

I. Kiến thức cần nhớ khi giải phương trình chứa dấu căn

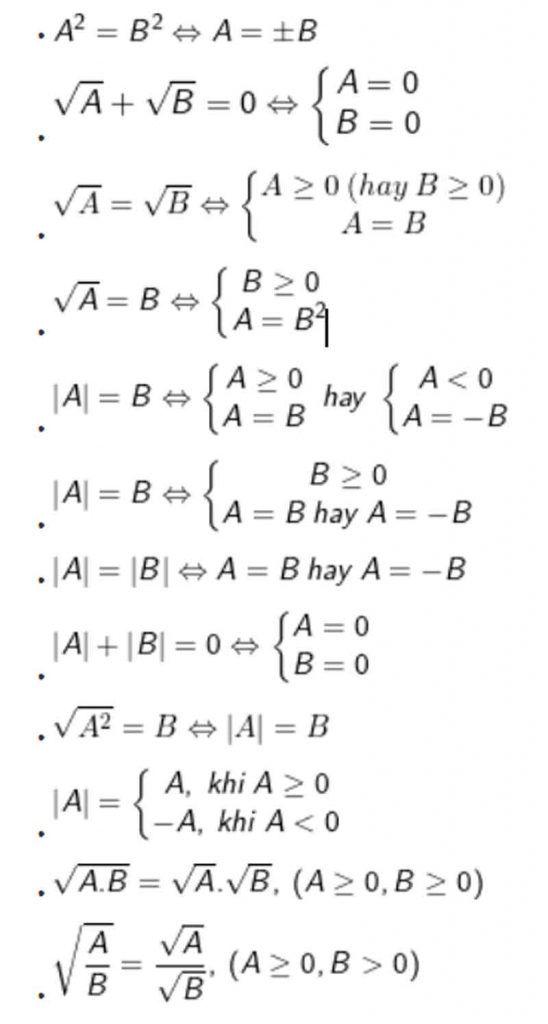
II. Cách giải Phương trình có chứa dấu căn

– Đối chiếu điều kiện (x < 1 hoặc x ≥ 3/2) ta thấy x = 1/2 thỏa điều kiện, nên ta nhận nghiệm này. Kết luận pt có nghiệm x = 1/2.

– Bước 2: Nhận dạng từng loại tương ứng với các cách giải sau:

¤ Loại 1: Nếu f(x) có dạng hằng đẳng thức (Ax ± B)2 thì khai căn đưa về phương trình trị tuyệt đối để giải.

¤ Loại 2: Nếu f(x) = Ax ± B và g(x) = Ex ± D thì dùng phương pháp bình phương 2 vế.

¤ Loại 3: Nếu f(x) = Ax2 + Bx + C [không có dạng hằng đẳng thức (Ax ± B)2] và g(x) = Ex ± D thì dùng phương pháp bình phương 2 vế.

¤ Loại 4: Nếu f(x) = Ax2 + Bx + C và g(x) = Ex2 + Dx + F thì thử phân tích f(x) và g(x) thành nhân tử, nếu chúng có nhân tử chung thì đặt nhân tử chung đưa về phương trình tích.

– Bước 3: Kiểm tra nghiệm tìm được có thỏa mãn điều kiện không sau đó kết luận nghiệm của phương trình.

– Bình phương 2 vế ta được:

2x – 3 = (x – 1)2 ⇔ 2x – 3 = x2 – 2x + 1

⇔ x2 – 4x + 4 = 0 ⇔ (x – 2)2 = 0 ⇔ x = 2.

– Đối chiếu với điều kiện ta thấy x = 2 thỏa điều kiện nên phương trình nhận nghiệm này.

– Phương trình có nghiệm x = 2.

° Lời giải:

– Ta thấy: f(x) = x2 – 5x – 6 không có dạng hằng đẳng thức (Ax ± B)2 (và vế phải là dạng hàm bậc 1) nên để khử căn ta dùng phương pháp bình phương 2 vế.

⇒ Phương trình có vô số nghiệm x ≥ 9.

– Đến đây xét các trường hợp giải tương tự ví dụ 1 ở trên.

4. Cách giải một số phương trình chứa căn khác.

i) Phương pháp đặt ẩn phụ để giải phương trình chứa dấu căn.

→ Phương trình có nghiệm x = 6.

→ Vậy phương trình có nghiệm x = -1.

III. Một số bài tập về phương trình có chứa dấu căn

* Bài 1: Giải các phương trình sau:

GIA SƯ TOÁN

Cách giải phương trình chứa ẩn dưới dấu căn – Toán lớp 10

Để giải phương trình chứa ẩn dưới dấu căn bậc 2, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.

Vậy chi tiết cách giải phương trình chứa ẩn dưới dấu căn như thế nào? chúng ta cùng tìm hiểu chi tiết qua bài viết dưới đây. Đồng thời vận dụng giải một số phương trình chứa ẩn trong dấu căn thức để rèn kỹ năng giải toán dạng này.

° Cách giải phương trình chứa ẩn dưới dấu căn (pt quy về pt bậc 2)

– Sử dụng phương pháp: Bình phương hai vế (nâng lên lũy thừa). Phép biến đổi là hệ quả nên khi tìm ra x, cần thay lại phương trình đã cho kiểm tra nghiệm.

– Hoặc sử dụng các phép biến đổi tương đương sau:

– Sử dụng phương pháp đặt ẩn phụ biến đổi đưa về phương trình bậc 2

– Có thể đưa về pt chứa dấu trị tuyệt đối, phương trình tích,…

° Vận dụng giải một số bài tập, ví dụ về phương trình chứa ẩn dưới dấu căn

* Bài tập 1 (Bài 7 trang 63 SGK Đại số 10): Giải các phương trình

* Cách 1: Sử dụng phương pháp nâng bậc.

– Điều kiện xác định: 5x + 6 ≥ 0 ⇔ x ≥ -6/5. Ta có

(1) ⇒ 5x + 6 = (x – 6)2 [Bình phương 2 vế]

⇔ 5x + 6 = x2 – 12x + 36

⇔ x2 – 17x + 30 = 0

Có: Δ = (-17)2 – 4.30 = 49 > 0 pt có 2 nghiệm: x1 = 15 ; x2 = 2.

– Đối chiếu điều kiện xác định ta thấy x1, x2 thỏa ĐKXĐ

– Thử lại: x = 15 thỏa nghiệm của (1); x = 2 không phải là nghiệm của (1).

¤ Kết luận: Phương trình có nghiệm x = 15.

* Cách 2: Sử dụng phép biến đổi tương đương.

– Thử lại thấy x = 2 không phải nghiệm của (2); x = -1 là nghiệm của (2).

¤ Kết luận: Phương trình có nghiệm duy nhất x = -1.

– Tập xác định: D=R (vì 4×2 + 2x + 10 >0 với mọi x).

(4) ⇒ 4×2 + 2x + 10 = (3x + 1)2

⇔ 4×2 + 2x + 10 = 9×2 + 6x + 1

⇔ 5×2 + 4x – 9 = 0

⇔ x = 1 hoặc x = -9/5

– Thử lại thấy chỉ có x = 1 là nghiệm của phương trình (4).

¤ Kết luận: Phương trình có nghiệm duy nhất x = 1.

* Bài tập 2: Giải các phương trình

– Điều kiện xác định: 25 – x2 ≥ 0 ⇔ -5 ≤ x ≤ 5.

(3) ⇒ 25 – x2 = (x – 1)2 (bình phương 2 vế)

⇔ 25 – x2 = x2 – 2x + 1

⇔ 2×2 – 2x – 24 = 0

⇔ x = 4 hoặc x = -3

– Đối chiếu với điều kiện xác định x = -3 và x = 4 thỏa ĐKXĐ

– Thử lại nghiệm chỉ có x = 4 thỏa.

¤ Kết luận: Phương trình có nghiệm duy nhất x = 4.

– Đối chiếu với điều kiện xác định x = 0 và x = -7/2 thỏa ĐKXĐ

– Thử lại nghiệm chỉ có x = 0 thỏa.

¤ Kết luận: Phương trình có nghiệm duy nhất x = 0.

* Lưu ý: – Khi bình phương hai vế có thể xuất hiện thêm nghiệm (gọi là nghiệm ngoại lai), ta cần thử lại nghiệm sau khi giải phương trình này.

Phương trình đã cho (*) trở thành:

t2 – 1 – t – 5 = 0 ⇔ t2 – t – 6 = 0

⇔ t = -2(loại) hoặc t = 3(nhận)

– Kết luận: Phương trình có 1 nghiệm x = 8.

Cách giải phương trình chứa dấu căn cực hay, có đáp án

Lý thuyết và Phương pháp giải

Phương trình chứa ẩn dưới dấu căn có nhiều cách giải, sau đây là một số phương pháp thường dùng:

+ Nâng lên lũy thừa

+ Đặt ẩn phụ

+ Đưa về phương trình chứa dấu giá trị tuyệt đối

+ Sử dụng bất đẳng thức, đánh giá hai vế của phương trình

Ví dụ minh họa

Ví dụ 1: Giải các phương trình sau:

Cách giải phương trình chứa ẩn dưới dấu căn cực hay, chi tiết

Lý thuyết & Phương pháp giải

Để giải phương trình chứa ẩn dưới dấu căn ta tìm cách để khử dấu căn, bằng cách:

– Nâng luỹ thừa hai vế.

– Phân tích thành tích.

– Đặt ẩn phụ.

Các dạng phương trình sau ta có thể giải bằng cách thực hiện phép biến đổi tương đương:

Phương trình chứa ẩn dưới dấu căn