Bài viết này chúng ta sẽ ôn lại các phương pháp dùng để tính góc giữa hai mặt phẳng, làm các bài tập vận dụng để hiểu rõ hơn.

° Cách tính góc giữa hai mặt phẳng

– Để tính góc giữa hai mặt phẳng (α) và (β) ta có thể thực hiện theo một trong các cách sau:

• Cách 1: Tìm hai đường thẳng a, b lần lượt vuông góc với hai mặt phẳng (α) và (β). Khi đó, góc giữa hai mặt phẳng (α) và (β) chính là góc giữa hai đường thẳng a và b.

• Cách 2: Sử dụng công thức hình chiếu: Gọi S là diện tích của hình (H) trong mp(α) và S’ là diện tích hình chiếu (H’) của (H) trên mp(β) thì S’ = S.cosφ ⇒ cosφ ⇒ φ

• Cách 3: Xác định góc giữa hai mặt phẳng rồi sử dụng hệ thức lượng trong tam giác để tính.

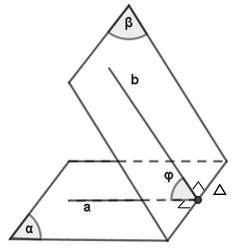
+ Bước 1: Tìm giao tuyến Δ của hai mặt phẳng

+ Bước 2: Dựng 2 đường thẳng a, b lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến Δ tại 1 điểm trên Δ (Tức là xác định mp phụ (γ) vuông góc Δ với (α) ∩ (γ) = a; (β) ∩ (γ) = b)), khi đó:

° Cách tính góc giữa hai mặt phẳng qua ví dụ minh họa

* Ví dụ 1: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Hãy xác định góc giữa hai mặt phẳng (ACD) và (BCD)?

* Lời giải:

– Ta có hình minh họa như sau: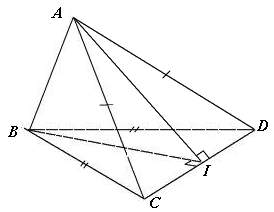

– Tam giác BCD cân tại B có I trung điểm đáy CD ⇒ CD ⊥ BI (1)

– Tam giác CAD cân tại A cóI trung điểm đáy CD ⇒ CD ⊥ AI (2)

– Từ (1) và (2) ⇒ CD ⊥ (ABI).

⇒ (BCD) ⊥ (ABI) và (ACD) ⊥ (ABI);

⇒ Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB.

* Ví dụ 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Tính góc giữa một mặt bên và mặt đáy.

* Lời giải:

– Ta minh họa như hình sau: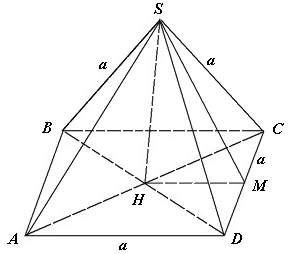

– Gọi H là giao điểm của AC và BD.

– Do S.ABCD là hình chóp tứ giác đều nên SH ⊥( ABCD)

Ta có: (SCD) ∩ (ABCD) = CD. Gọi M là trung điểm CD.

– Tam giác SCD là cân tại S; tam giác CHD cân tại H (tính chất đường chéo hình vuông)

SM ⊥ CD và HM ⊥ CD

⇒ ((SCD), (ABCD)) = (SM, HM) = ∠SMH = α

– Từ giả thiết suy ra tam giác SCD là tam giác đều cạnh a có SM là đường trung tuyến

* Ví dụ 3: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng a. Gọi M là trung điểm SC. Tính góc giữa hai mặt phẳng (MBD) và (ABCD).

* Lời giải:

– Minh họa như hình vẽ sau: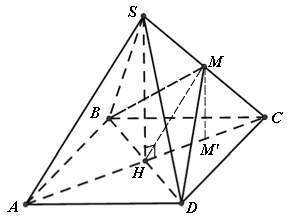

– Do S.ABCD là hình chóp tứ giác đều nên SH ⊥ (ABCD) ⇒ SH ⊥ HC.

– Xét tam giác SHC vuông tại H đường trung tuyến SM ta có:

;

– Gọi M’ là hình chiếu của M lên mặt phẳng (ABCD)

(MM’ là đường trung bình của ΔSHC)

Do đó:

* Ví dụ 4: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA = a và SA ⊥ (ABC), AB = BC = a. Tính góc giữa hai mặt phẳng (SAC) và (SBC).

* Lời giải:

– Minh họa như hình vẽ sau:

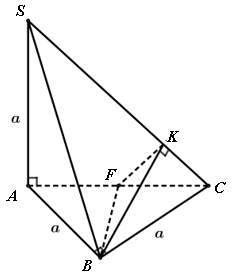– Ta có: (SAC) ∩ (SBC) = SC

– Gọi F là trung điểm AC ⇒ BF ⊥ AC

Lại có BF ⊥ SA ⇒ BF ⊥ (SAC)

– Kẻ BK ⊥ SC tại K, SC ⊥ BF suy ra SC ⊥ (BKF).

– Vì ΔBFK vuông tại F

* Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Tính góc giữa hai mặt phẳng (SBD) và (ABCD).

* Lời giải:

– Minh họa như hình vẽ sau: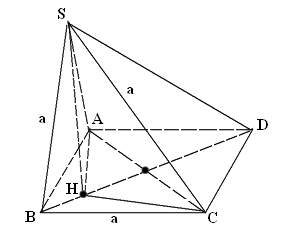– Gọi H là chân đường vuông góc của S xuống mặt phẳng đáy (ABCD) (SH ⊥(ABCD))

– Theo bài ra, SA = SB = SC = a nên hình chiếu vuông góc của S lên mp(ABCD) là H cũng chính là tâm đường tròn ngoại tiếp tam giác ABC (do HA = HB = HC).

– Cũng theo bài ra, ta có: AB = BC = a ⇒ ΔABC cân tại B

⇒ tâm H phải nằm trên BD (BD đường chéo của hình thoi ABCD nên BD cũng là là đường trung trực của AC)

⇒ SH ⊂ (SBD); lại có SH ⊥ (ABCD) nên

⇒ (SBD) ⊥ (ABCD)