I. Tính diện tích hình phẳng

1. Hình phẳng giới hạn bởi một đường cong và trục hoành

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a; x = b được xác định: S=∫ab|f⁢(x)|⁢𝑑x.

Ví dụ 1. Tính diện tích hình phẳng được giới hạn bởi y = 5×4 + 3×2, trục hoành và hai đường thẳng x = 0; x = 1.

Lời giải:

Diện tích hình phẳng cần tính là:

S=∫01|  5⁢x4+ 3⁢x2|⁢𝑑x=∫01(5⁢x4+ 3⁢x2)⁢𝑑x=(x5+x3)|01= 2

2. Hình phẳng được giới hạn bởi 2 đường cong

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a; x = b được xác định:

S=∫ab|f⁢(x)-g⁢(x)|⁢𝑑x (*).

– Chú ý.

Khi áp dụng công thức (*), cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Muốn vậy ta giải phương trình: f(x) – g(x) = 0 trên đoạn [a; b].

Giả sử phương trình có hai nghiệm c; d (c < d). Khi đó, f(x) – g(x) không đổi dấu trên các đoạn [a; c]; [c; d]; [d; b]. Trên mỗi đoạn đó, chẳng hạn trên [a; c] ta có:

∫ac|f⁢(x)-g⁢(x)|⁢𝑑x=|∫ac[f⁢(x)-g⁢(x)]⁢𝑑x|.

Ví dụ 2. Tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = 0; x = 2 và các đồ thị của hai hàm số y = x – 1 và y = x2 – 1.

Lời giải:

Phương trình hoành độ giao điểm của hai đường cong:

x – 1 = x2 – 1

⇔x-x2=  0⇔[x=0x= 1∈[0; 2]

Diện tích hình phẳng đã cho là:

S=∫02|x-1-(x2-1)|⁢𝑑x=∫02|x-x2|⁢𝑑x=∫01|x-x2|⁢𝑑x+∫12|x-x2|⁢𝑑x

=|∫01(x-x2)⁢𝑑x|+|∫12(x-x2)⁢𝑑x|=|(x22-x33)|01⁢|+|(x22-x33)|12|

=16+|-23-16|= 1.

II. Tính thể tích

1. Thể tích của vật thể

Cắt một vật thể (H) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a; x = b (a < b) . Một mặt phẳng tùy ý vuông góc với Ox tại điểm x (a≤x≤b)cắt (H) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a; b].

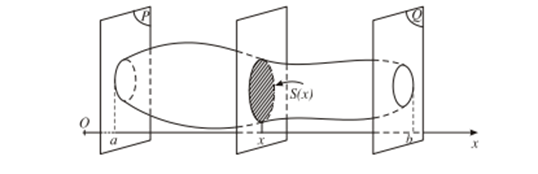
Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng (P) và (Q) được xác định bởi công thức: V=∫abS⁢(x)⁢𝑑x.

2. Thể tích khối chóp và khối chóp cụt.

a) Cho khối chóp có diện tích đáy là B, chiều cao h.

Khi đó, thể tích của khối chóp là V=13⁢B.h.

b) Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B; B’ và chiều cao là h.

Thể tích của khối chóp cụt là:

V=h3⁢(B+B.B’+B’)

III. Thể tích khối tròn xoay

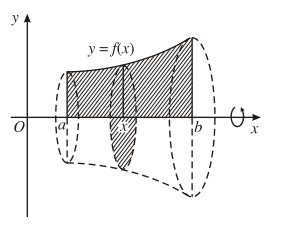
– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường cong y = f(x), trục hoành và hai đường thẳng x = a; x = b quanh trục Ox:

V=π⁢∫abf2⁢(x)⁢𝑑x.

Ví dụ 3. Cho hình phẳng giới hạn bởi đường cong y=x2, trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích khối tròn xoay thu được khi quay hình này quanh trục Ox.

Lời giải:

Thể tích khối tròn xoay cần tính là:

V=π⁢∫02×4⁢𝑑x=π⁢x55|02=32⁢π5.